
Урок "Определение синуса и косинуса на единичной окружности"

Краткое описание документа:
Видеоурок «Определение синуса и косинуса на единичной окружности» представляет наглядный материал для урока по соответствующей теме. В ходе урока рассматриваются понятия синуса и косинуса для чисел, соответствующих точкам единичной окружности, описывается множество примеров, формирующих умение решать задания, где используется данная интерпретация понятий. Удобное и понятное иллюстрирований решений, подробно описанный ход рассуждений помогают быстрее достичь целей обучения, повысить эффективность урока.
Видеоурок начинается с представления темы. В начале демонстрации дается определение синуса и косинуса числа. На экране демонстрируется единичная окружность с центром в начале координат, отмечаются точки пересечения единичной окружности с осями координат А, В, С, D. В рамке выделено определение, в котором указано, что если точке М, принадлежащей единичной окружности, соответствует некоторое число t, то абсцисса этой точки является косинусом числа t и обозначается cos t, ордината точки является синусом и обозначается sin t. Озвучивание определения сопровождается изображением на единичной окружности точки М, указанием ее абсциссы и ординаты. Представляется краткая запись с помощью обозначений, что для М(t)=M(x;y), х= cos t, у= sin t. Указываются ограничения, накладываемые на значение косинуса и синуса числа. Согласно рассмотренным данным, -1<=cos t<=1 и -1<= sin t<=1.
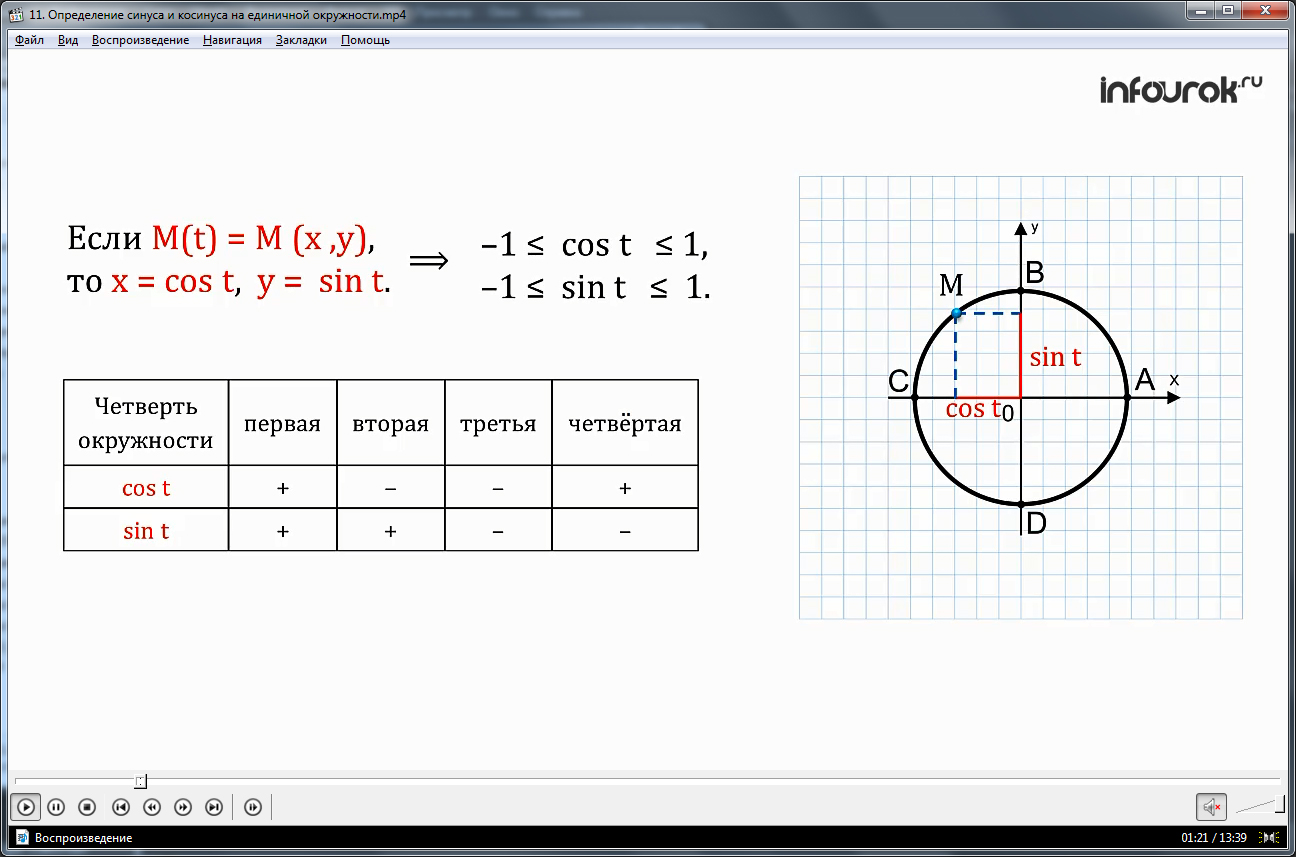
Также по рисунку легко отследить, как изменяется знак функции в зависимости от того, в какой четверти располагается точка. На экране составляется таблица, в которой для каждой функции указывается ее знак в зависимости от четверти. Знак cos t - плюс в первой и четвертой четвертях и минус во второй и третьей четвертях. Знак sin t - плюс в первой и второй четвертях, минус в третьей и четвертой четвертях.
Ученикам напоминается уравнение единичной окружности х2+у2=1. Отмечается, что после подстановки вместо координат соответствующих функций, получим cos2t+ sin2t=1 – основное тригонометрическое тождество. Пользуясь способом нахождения sin t и cos t с помощью единичной окружности, заполняется таблица основных значений синуса и косинуса для чисел от 0 до 2π с шагом π/4 и для чисел от π/6 до 11π/6 с шагом π/6. На экране демонстрируются эти таблицы. С помощью их и рисунка учитель может проверить, как усвоен материал и насколько ученикам понятно происхождение значений sin t и cos t.
Рассматривается пример, в котором вычисляется sin t и cos t для t=41π/4. Решение иллюстрируется рисунком, на котором изображена единичная окружность с центром в начале координат. На ней отмечается точка 41π/4. Замечено, что данная точка совпадает с положением точки π/4. Это доказывается с помощью представления данной дроби в виде смешанной 41π/4=π/4+2π·5. Пользуясь таблицей значений косинуса, получаем значения cos π/4=√2/2 и sinπ/4=√2/2. Из полученных сведений следует, что cos 41π/4=√2/2 и sin 41π/4=√2/2.
В втором примере необходимо вычислить sin t и cos t для t=-25π/3. На экране изображается единичная окружность с отмеченной на ней точкой t=–25π/3. Сначала для решения задания число –25π/3 представляется в виде смешанной дроби, чтобы обнаружить, какому табличному значению будет соответствовать его sin t и cos t. После преобразования получаем –25π/3=-π/3+2π·(-4). Очевидно, t=-25π/3 совпадет на окружности с точкой –π/3 или 5π/3. Из таблицы выбираем соответствующие значения синуса и косинуса cos 5π/3=1/2 и sin 5π/3=-√3/2. Эти значения будут верными и для рассматриваемого числа cos (-25π/3)=1/2 и sin (-25π/3)=-√3/2. Задача решена.
Аналогично решается и пример 3, в котором необходимо вычислить sin t и cos t для t=37π. Чтобы решить пример, число 37π раскладывается, вычленяя π и 2π. В таком представлении получается 37π=π+2π·18. На единичной окружности, которая изображена рядом с решением, отмечается данная точка на пересечении отрицательной части оси ординат и единичной окружности – точка π. Очевидно, что значения синуса и косинуса числа совпадут с табличными значениями π. Из таблицы находим значения sin π=-1 и cos π=0. Соответственно, эти же значения являются искомыми, то есть sin 37π=-1 и cos 37π=0.
В примере 4 требуется вычислить sin t и cos t при t=-12π. Представляем число в виде -12π=0+2π·(-6). Соответственно, точка -12π совпадает с точкой 0. Значения косинуса и синуса этой точки sin 0=1 и cos 0=0. Эти значения и являются искомыми sin (-12π)=1 и cos (-12π)=0.
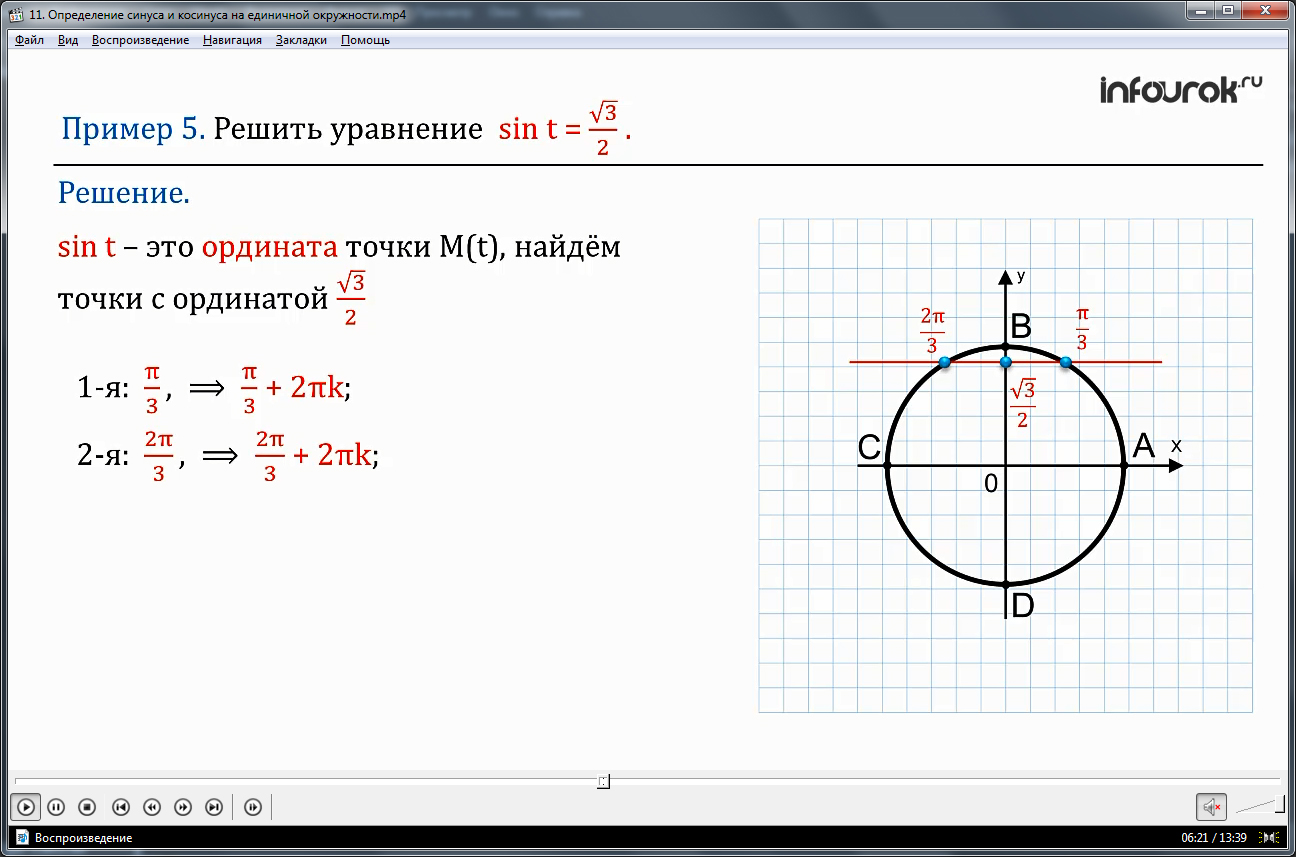
В пятом примере нужно решить уравнение sin t=√3/2. В решении уравнения используется понятие синуса числа. Так как он представляет ординату точки М(t), то необходимо отыскать точку с ординатой √3/2. На рисунке, сопровождающем решение, видно, что ординате √3/2 соответствуют две точки – первая π/3 и вторая 2π/3. Учитывая периодичность функции, отмечаем, что t=π/3+2πk и t= 2π/3+2πk для целого k.
В примере 6 решается уравнение с косинусом - cos t=-1/2. В поиске решений уравнения находим на единичной окружности точки с абсциссой 2π/3. На экране демонстрируется рисунок, на котором отмечается абсцисса -1/2. Ей соответствуют две точки на окружности - 2π/3 и -2π/3. Учитывая периодичность функций, найденное решение записывается в виде t=2π/3+2πk и t=-2π/3+2πk, где k- целое число.
В примере 7 решается уравнение sin t-1=0. Чтобы найти решение, уравнение преобразуется к виду sin t=1. Синусу 1 соответствует число π/2. Учитывая периодичность функции, найденное решение записывается в виде t=π/2+2πk, где k – целое. Аналогично в примере 8 решается уравнение cos t+1=0. Преобразуем уравнение к виду cos t=-1. Точка, абсцисса которой равна -1, соответствует числу π. Эта точка отмечена на единичной окружности, изображенной рядом с текстовым решением. Соответственно, решением данного уравнения является число t=π+2πk, где k – целое число. Не более сложным является решение уравнения cos t+1=1 в примере 9. Преобразовав уравнение, получаем cos t=0. На единичной окружности, изображенной рядом с решением, отмечаем точки –π/2 и -3π/2, в которых косинус принимает значение 0. Очевидно, решением данного уравнение будет ряд значений t=π/2+πk, где k – целое число.
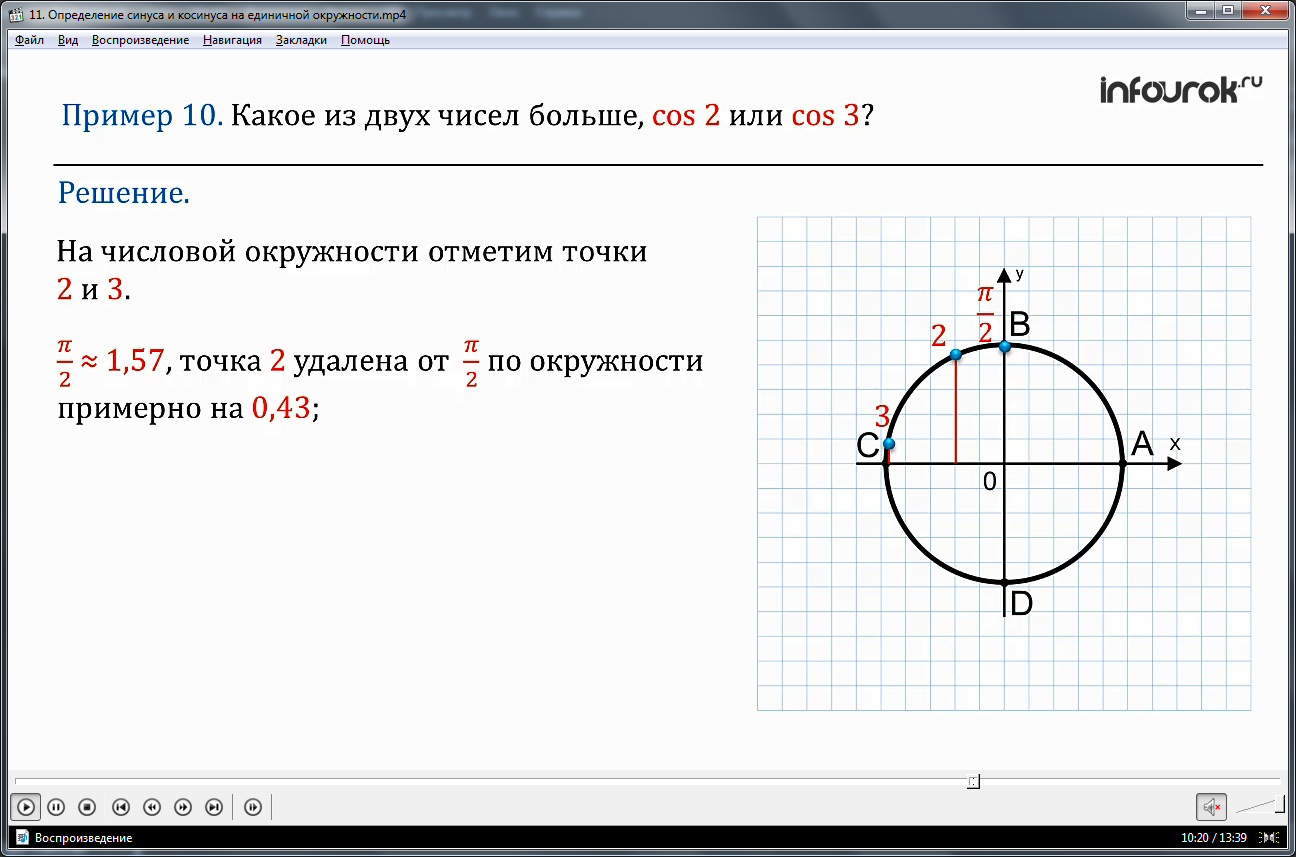
В примере 10 сравниваются значения sin 2 и cos 3. Чтобы решение было наглядным, демонстрируется рисунок, где отмечены точки 2 и 3. Зная, что π/2≈1,57, оцениваем удаленность точек от нее. На рисунке отмечается, что точка 2 удалена от π/2 на 0,43, в то время как 3 удалена на 1,43, поэтому точка 2 имеет большую абсциссу, чем точка 3. Это значит, что sin 2>cos 3.
Пример 11 описывает вычисление выражения sin 5π/4. Так как 5π/4 – это π/4+π, то, используя формулы приведения, выражение можно преобразовать в вид - sin π/4. Из таблицы выбираем его значение - sin π/4=-√2/2. Аналогично в примере 12 находится значение выражения cos7π/6. Преобразуя его к виду cos(π/6+π), получаем выражение – cos π/6. Табличное значение – cos π/6=-√3/2. Это значение и будет решением.
Далее предлагается запомнить важные равенства, которые помогают в решении задач – это sin(-t)= -sin t и cos (-t)=cos t. Фактически данное выражение отображает четность косинуса и нечетность синуса. На изображении единичной окружности рядом с равенствами можно увидеть, как на координатной плоскости работают данные равенства. Также представляются два равенства, отображающие периодичность функций, важные для решения задач sin(t+2πk)= sin t и cos (t+2πk)=cos t. Демонстрируются равенства, отображающие симметричное расположение точек на единичной окружности sin(t+π)= -sin t и cos (t+π)=-cos t. Рядом с равенствами строится изоражение, на котором отображается расположение этих точек на единичной окружности. И последние представленные равенства sin(t+π/2)= cos t и cos (t+π/2)=- sin t.
Видеоурок «Определение синуса и косинуса на единичной окружности» рекомендуется применять на традиционном школьном уроке математик для повышения его эффективности, обеспечения наглядности объяснения учителя. С этой же целью материал может использоваться в ходе дистанционного обучения. Пособие также может быть полезно для формирования соответствующих навыков решения заданий у учеников при самостоятельном освоении материала.
ТЕКСТОВАЯ РАСШИФРОВКА:
«Определение синуса и косинуса на единичной окружности».
Дадим определение синуса и косинуса числа
ОПРЕДЕЛЕНИЕ: если точка М числовой единичной окружности соответствует числу t(тэ), то абсциссу точки М называют косинусом числа t(тэ) и обозначают cost, а ординату точки М называют синусом числа t(тэ) и обозначают sint(рис).
Значит, если М(t) = М (x ,y)(эм от тэ равно эм с координатами икс и игрек), то x = cost, y= sint (икс равен косинус тэ, игрек равен синус тэ).Следовательно, -1≤ cost ≤ 1, -1≤ sint ≤1( косинус тэ больше либо равно минус один, но меньше либо равно один ; синус тэ больше либо равно минус один, но меньше либо равно один).Зная, что каждая точка числовой окружности имеет в системе xOy свои координаты, можно составить таблицу значении синуса и косинуса по четвертям окружности, где значение косинуса положительно в первой и четвертой четвертях и, соответственно, отрицательно во второй и третьей четвертях.
Значение синуса положительно в первой и второй четвертях и, соответственно, отрицательно в третьей и четвертой четвертях. (показать на чертеже)
Так как уравнение числовой окружности имеет вид х2 + у2 =1( икс квадрат плюс игрек квадрат равно одному), то получаем равенство:
(косинус квадрат тэ плюс синус квадрат тэ равно единице).
Опираясь на таблицы, которые мы составляли при определении координат точек числовой окружности, составим таблицы для координат точек числовой окружности для значений cost и sint .
Рассмотрим примеры.
ПРИМЕР 1. Вычислить cos t и sin t, если t = (тэ равно сорок один пи на четыре).
Решение. Числу t = соответствует та же точка числовой окружности, что и числу , так как = ∙π = ( 10 + ) ∙π = + 2π ∙ 5( сорок один пи на четыре равно сумме пи на четыре и произведения два пи на пять). А для точки t = по таблице значение косинусов 1 имеем cos = и sin =. Следовательно,
cos = и sin =
ПРИМЕР 2. Вычислить cos t и sin t, если t = (тэ равно минус двадцать пять пи на три).
РЕШЕНИЕ: Числу t = соответствует та же точка числовой окружности, что и числу , так как = ∙ π = – (8 + )∙π = + 2π ∙ ( – 4 ) ( минус двадцать пять пи на три равно сумме минус пи на три и произведению двух пи на минус четыре). А числу соответствует на числовой окружности та же точка, что и числу . А для точки t = по таблице 2 имеем cos = и sin = .Следовательно, cos () = и sin () =.
ПРИМЕР 3. Вычислить cos t и sin t, если t = 37π; ( тэ равно тридцать семь пи).
РЕШЕНИЕ: 37π = 36π + π = π + 2π ∙ 18.Значит, числу 37π соответствует та же точка числовой окружности, что и числу π. А для точки t = π по таблице 1 имеем cos π = –1, sin π=0.Значит, cos37π = –1, sin37π=0.
ПРИМЕР 4. Вычислить cos t и sin t, если t = –12π (равно минус двенадцать пи).
РЕШЕНИЕ: – 12π = 0 + 2π ∙ ( – 6), то есть числу – 12π соответствует та же точка числовой окружности, что и числу ноль. А для точки t = 0 по таблице 1 имеем cos 0 = 1, sin 0 =0.Значит, cos( –12π) =1, sin( –12π) =0.
ПРИМЕР 5. Решить уравнение sin t = .
Решение. Учитывая, что sin t – это ордината точки М(t) (эм от тэ) числовой окружности, найдем на числовой окружности точки с ординатой и запишем каким числам t они соответствуют. Одна точка соответствует числу , а значит, и любому числу вида + 2πk. Вторая точка соответствует числу , а значит, и любому числу вида + 2πk. Ответ: t = + 2πk,где kϵZ (ка принадлежит зэт),t= + 2πk,где kϵZ (ка принадлежит зэт).
ПРИМЕР 6. Решить уравнение cos t = .

Решение. Учитывая, что cos t – это абсцисса точки М(t) (эм от тэ) числовой окружности, найдем на числовой окружности точки с абсциссой и запишем каким числам t они соответствуют. Одна точка соответствует числу ,а значит и любому числу вида + 2πk. А вторая точка соответствует числу или , а значит, и любому числу вида + 2πk или + 2πk.
Ответ: t = + 2πk, t=+ 2πk ( или ± + 2πk( плюс минус два пи на три плюс два пи ка) , где kϵZ (ка принадлежит зэт).
ПРИМЕР 7.Решить уравнение cos t = .
Решение. Аналогично предыдущему примеру, на числовой окружности нужно найти точки c абсциссой и записать, каким числам t они соответствуют.
По рисунку видно, что абсциссу имеют две точки Е и S, а каким числам они соответствуют мы пока не сможем сказать. К этому вопросу вернемся позже.
ПРИМЕР 8.Решить уравнение sin t = – 0,3.
Решение. На числовой окружности найдем точки с ординатой – 0,3 и запишем , каким числам t они соответствуют.
Ординату – 0,3 имеют две точки P и H, а каким числам они соответствуют мы пока не сможем сказать. К этому вопросу так же вернемся позже.
ПРИМЕР 9.Решить уравнение sin t –1 =0
Решение. Перенесем минус единицу в правую часть уравнения, получим синус тэ равно одному ( sin t =1). На числовой окружности нам нужно найти точку, у которой ордината равна один. Эта точка соответствует числу , а значит всем числам вида + 2πk( пи на два плюс два пи ка).
Ответ: t = + 2πk, kϵZ( ка принадлежит зэт).
ПРИМЕР 10.Решить уравнение cos t + 1 = 0.
Перенесем единицу в правую часть уравнения, получим косинус тэ равно минус один(cos t = – 1).Абсциссу минус один имеет точка числовой окружности, которая соответствует числу π, а это значит, и все числам вида π+2πk. Ответ: t = π+ 2πk, kϵZ.
ПРИМЕР 11. Решить уравнение cos t + 1 = 1.
Перенесем единицу в правую часть уравнения, получим косинус тэ равно нулю(cos t = 0).Абсциссу ноль имеют точки В и D (рис 1), которые соответствуют числам , , , , и т. д. Эти числа можно записать так + πk. Ответ : t = + πk, kϵZ.
ПРИМЕР 12. Какое из двух чисел больше, cos 2 или cos 3? (косинус двух или косинус трех)
Решение. Переформулируем вопрос по-другому: на числовой окружности отмечены точки 2 и 3. У какой из них абсцисса больше?
На числовой окружности отметим точки 2 и 3. Вспомним, что .Значит, точка 2 удалена от по окружности примерно на 0,43( нуль целых сорок три сотых) ( 2 –≈ 2 – 1,57 = 0,43), а точка 3 на 1,43 (одну целую сорок три сотых). Следовательно, точка 2 находится ближе к точке , чем точка 3, поэтому у нее абсцисса больше (мы учли, что абсциссы обе отрицательные).
Ответ: cos 2 > cos 3.
ПРИМЕР 13. Вычислить sin (синус пять пи на четыре)
Решение. sin( + π) = – sin = (синус пять пи на четыре равно сумме пи на четыре и пи равно минус синус пи на четыре равно минус корень из двух на два).
ПРИМЕР 14. Вычислить cos (косинус семь пи на шесть).
cos( + π ) = – cos =. (представили семь пи на шесть как сумму пи на шесть и пи и применили третье равенство).
Для синуса и косинуса получим некоторые важные формулы.
1. Для любого значения t справедливы равенства
sin (–t) = –sin t
cos (–t) = cos t
Синус от минус тэ равно минус синус тэ
Косинус от мину тэ равно косинусу тэ.
По рисунку видно, что у точек Е и L, симметричных относительно оси абсцисс, одна и та же абсцисса, это значит
cos(–t) = cost, но равны по модулю и противоположные по знаку ординаты (это значит sin(– t) = – sint.
2. Для любого значения t справедливы равенства
sin (t+2πk) = sin t
cos (t+2πk) = cos t
Синус от тэ плюс два пи ка равно синусу тэ
Косинус от тэ плюс два пи ка равно косинусу тэ
Это верно, так как числам t и t+2πk соответствует одна и та же точка.
3. Для любого значения t справедливы равенства
sin (t+π) = –sin t
cos (t+π) = –cos t
Синус от тэ плюс пи равно минус синусу тэ
косинус от тэ плюс пи равно минус косинусу тэ
Пусть числу t соответствует точка E числовой окружности, тогда числу t+π соответствует точка L, которая симметрична точке E относительно начала координат. По рисунку видно, что у этих точек абсциссы и ординаты равны по модулю и противоположны по знаку. Это значит,
cos(t +π)= – cost;
sin(t +π)= – sint.
4. Для любого значения t справедливы равенства
sin (t+) = cos t
cos (t+) = –sin t
Синус тэ плюс пи на два равно косинусу тэ
Косинус тэ плюс пи на два равно минус синусу тэ.
| Автор | |
|---|---|
| Дата добавления | 27.07.2014 |
| Раздел | Алгебра |
| Подраздел | Видеоурок |
| Просмотров | 14291 |
| Номер материала | 834 |