
Урок "Тригонометрические функции числового аргумента"

Краткое описание документа:
Видеоурок «Тригонометрические функции числового аргумента» представляет наглядный материал для обеспечения наглядности при объяснении темы на уроке. В ходе демонстрации рассматривается принцип формирования значения тригонометрических функций от числа, описывается ряд примеров, обучающих вычислению значений тригонометрических функций от числа. С помощью данного пособия легче сформировать навыки в решении соответствующих задач, добиться запоминания материала. Использование пособия повышает эффективность урока, способствует быстрому достижению целей обучения.
В начале урока демонстрируется название темы. Затем ставится задача нахождения соответствующего косинуса некоторому числовому аргументу. Отмечается, что данная задача решается просто и это можно наглядно продемонстрировать. На экране изображается единичная окружность с центром в начале координат. При этом замечено, что точка пересечения окружности с положительной полуосью оси абсцисс располагается в точке А(1;0). Приводится пример точки М, которая представляет аргумент t=π/3. Данная точка отмечается на единичной окружности, и от нее опускается перпендикуляр к оси абсцисс. Найденная абсцисса точки и является косинусом cos t. В данном случае абсциссой точки будет х=1/2. Поэтому cos t=1/2.
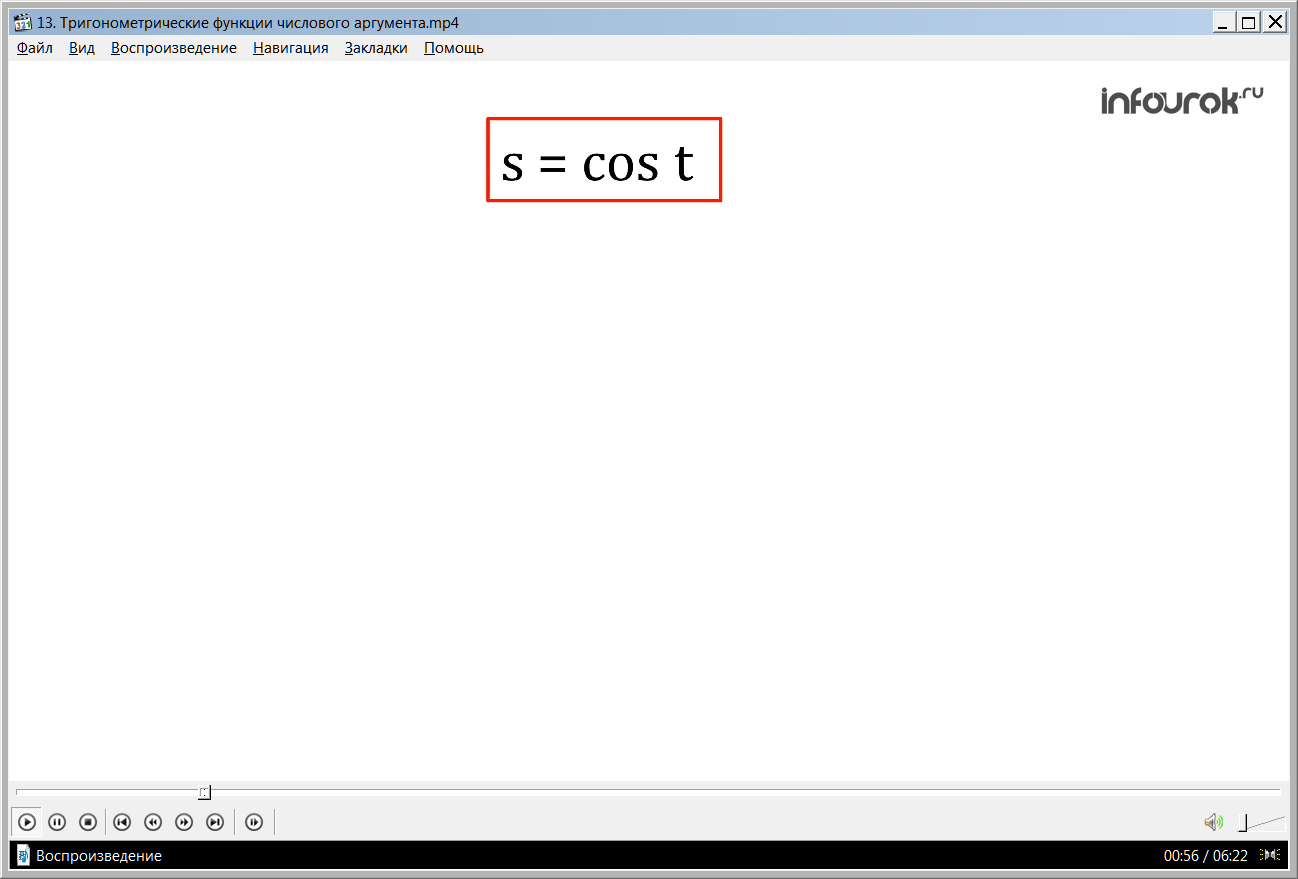
Обобщая рассмотренные факты, отмечается, что имеет смысл говорить о функции s=cos t. Отмечается, что некоторые знания об этой функции уже имеются у учеников. Вычислены некоторые значения косинуса cos 0=1, cos π/2=0, cos π/3=1/2. Также связанными к данной функцией являются функции s=sin t, s=tg t, s=ctg t. Отмечается, что они имеют общее для всех название – тригонометрические функции.
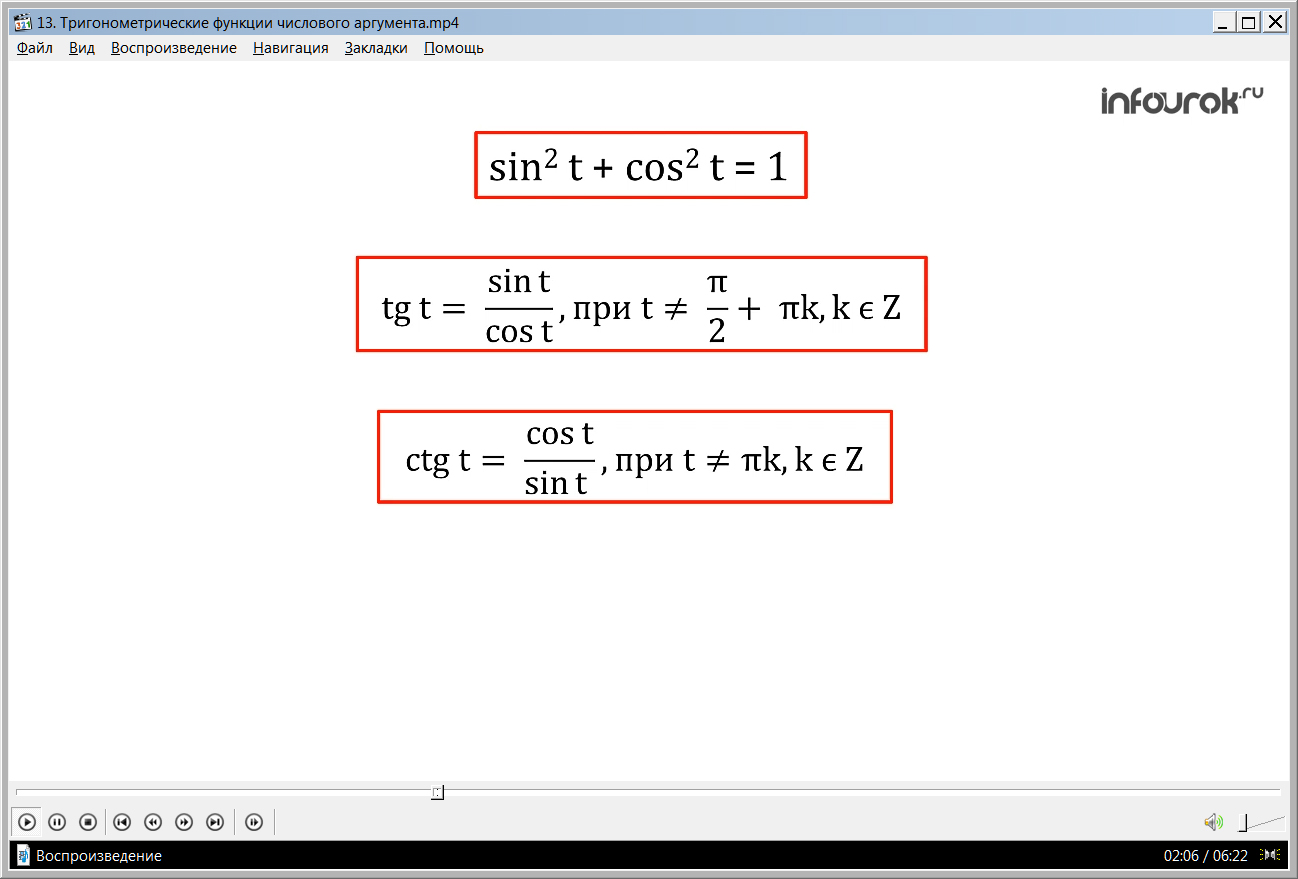
Демонстрируются важные соотношения, которые используются в решении задач с тригонометрическими функциями: основное тождество sin2t+ cos2t=1, выражение тангенса и котангенса через синус и косинус tg t=sin t/cos t, где t≠π/2+πk для kϵZ, ctg t= cos t/sin t, где t≠πk для kϵZ, а также соотношение тангенса к котангенсу tg t·ctg t=1 где t≠πk/2 для kϵZ.
Далее предлагается рассмотреть доказательство соотношения 1+ tg2t=1/ cos2t, при t≠π/2+πk для kϵZ. Чтобы доказать тождество, необходимо представить tg2t в виде соотношения синуса и косинуса, а после слагаемые в левой части привести к общему знаменателю 1+ tg2t=1+sin2t/cos2t = (sin2t+cos2t)/ cos2t. Используя основное тригонометрическое тождество, получаем в числителе 1, то есть конечное выражение 1/ cos2t. Что и требовалось доказать.
Аналогично доказывается тождество 1+ ctg2t=1/ sin 2t, при t≠πk для kϵZ. Так же, как и в предыдущем доказательстве, котангенс заменяется соответствующим соотношением косинуса и синуса, и оба слагаемых в левой части приводятся к общему знаменателю 1+ ctg2t=1+ cos2t/sin2t= (sin2t+cos2t)/sin 2t. После применения основного тригонометрического тождества к числителю получаем 1/ sin 2t. Это и есть искомое выражение.
Рассматривается решение примеров, в котором применяются полученные знания. В первом задании необходимо найти значения cost, tgt, ctgt, если известен синус числа sint=4/5, а t принадлежит промежутку π/2< t<π. Для нахождения косинуса в данном примере рекомендуется использовать тождество sin2t+ cos2t=1, из которого следует cos2t=1-sin2t. Зная значение синуса, можно найти косинус cos2t=1-(4/5)2=9/25. То есть значение косинуса cost=3/5 и cost=-3/5. В условии указано, что аргумент принадлежит второй четверти координатной плоскости. В этой четверти значение косинуса отрицательное. С учетом данного ограничения находим cost=-3/5. Для нахождения тангенса числа пользуемся его определением tgt= sint/cost. Подставив известные значения синуса и косинуса, получаем tgt=4/5:(-3/5)=-4/3. Чтобы найти значение котангенса, также используется определение котангенса ctgt= cost/sint. Подставив известные значения синуса и косинуса в отношение, получаем ctgt=(-3/5):4/5=-3/4.
Далее рассматривается решение аналогичной задачи, в которой известен тангенс tgt=-8/15, а аргумент ограничен значениями 3π/2<t<2π. Необходимо найти значения cost, sint, ctgt. Чтобы решить задачу, используем тождество 1+ tg2t=1/ cos2t. Подставив известное значение тангенса в формулу, находим значение косинуса cos2t=1+(-8/15)2=225/289. Отсюда cost=15/17 и cost=-15/17. Так как аргумент принадлежит четвертой четверти, с учетом этого ограничения cost=15/17.
Чтобы найти значение синуса, используем определение тангенса tgt= sint/cost. Из него находим sint= tgt·cost=(-8/15)·(15/17)=-8/17. Зная, что котангенс – функция, обратная тангенсу, находим ctgt=1/(-8/15)=-15/8.
Видеоурок «Тригонометрические функции числового аргумента» применяется для повышения эффективности урока математики в школе. В ходе дистанционного обучения данный материал может использоваться как наглядное пособие для формирования навыков решения задач, где есть тригонометрические функции от числа. Для приобретения этих навыков ученику может рекомендовано самостоятельное рассмотрение наглядного материала.
ТЕКСТОВАЯ РАСШИФРОВКА:
Тема урока «Тригонометрические функции числового аргумента».
Любому действительному числу t можно поставить в соответствие однозначно определенное число cos t. Для этого необходимо выполнить следующие действия:
1) на координатной плоскости расположить числовую окружность так, чтобы центр окружности совпал с началом координат, а начальная точка А окружности попала в точку (1;0);
2) на окружности найти точку, которая соответствует числу t;
3) найти абсциссу этой точки. Это и есть cos t.
Поэтому речь пойдет о функции s= cos t ( эс равно косинус тэ), где t – любое действительное число. Некоторое представление о этой функции мы уже получили:
- научились вычислять некоторые значения, например cos 0=1, cos = 0, cos = и т.д.( косинус нуля равен единице, косинус пи на два равен нулю, косинус пи на три равен одной второй и так далее).
- а так как значения синуса, косинуса, тангенса и котангенса взаимосвязаны, то получили некоторое представление еще о трех функциях: s= sint; s= tgt; s= ctgt. (эс равно синус тэ, эс равно тангенс тэ, эс равно котангенс тэ)
Все эти функции называются тригонометрическими функциями числового аргумента t.
Из определений синуса, косинуса, тангенса и котангенса следуют некоторые соотношения:
1)sin2t + cos2t = 1( синус квадрат тэ плюс косинус квадрат тэ равно одному)
2)tgt = при t ≠ + πk, kϵZ( тангенс тэ равно отношению синуса тэ к косинусу тэ при тэ не равном пи на два плюс пи ка, ка принадлежит зэт)
3)ctgt = при t ≠ πk, kϵZ( котангенс тэ равно отношению косинуса тэ к синусу тэ при тэ не равном пи ка, ка принадлежит зэт).
4)tgt ∙ ctgt = 1 при t ≠ , kϵZ (произведение тангенса тэ на котангенс тэ равно одному при тэ не равном пи ка, деленное на два, ка принадлежит зэт)
Докажем еще две важные формулы:
|
Один плюс тангенс квадрат тэ равно отношению единицы к косинусу квадрату тэ при тэ не равном пи на два плюс пи ка.
|
|
Доказательство. 1+ tg 2 t =
Выражение единица плюс тангенс квадрат тэ, приведем к общему знаменателю косинус квадрат тэ. Получим в числителе сумму квадратов косинуса тэ и синуса тэ, что равно одному. А знаменатель остается квадрат косинуса тэ. |
|
Сумма единицы и квадрата котангенса тэ равна отношению единицы к квадрату синуса тэ при тэ не равном пи ка.
|
|
Доказательство. Выражение единица плюс котангенс квадрат тэ, аналогично приведем к общему знаменателю и применим первое соотношение. |
Рассмотрим примеры.
ПРИМЕР1. Найти cost, tgt, ctgt , если sint = и < t < π.( если синус тэ равен четырем пятым и тэ из промежутка от пи на два до пи)
Решение. Из первого соотношения найдем косинус квадрат тэ равен единица минус синус квадрат тэ: cos2t = 1 – sin2t.
Значит, cos2t = 1 –( )2 = ( косинус квадрат тэ равен девяти двадцать пятым), то есть cost= ( косинус тэ равен трем пятым) или cost = – (косинус тэ равен минус трем пятым). По условию аргумент t принадлежит второй четверти, а в ней cos t < 0 ( косинус тэ отрицательный).
Значит косину тэ равен минус трем пятым, cost = – .
Вычислим тангенс тэ:
tgt = = ׃ (– )= – ;( тангенс тэ равен отношению синуса тэ к косинусу тэ, а значит , четырех пятых к минус трем пятым и равно минус четырем третьим)
Соответственно вычисляем (котангенс числа тэ. так как котангенс тэ равен отношению косинуса тэ к синусу тэ,) ctgt = = – .
( котангенс тэ равен минус трем четвертым).
Ответ : cost = – , tgt= – ; ctgt = – . (ответ заполняем по мере решения)
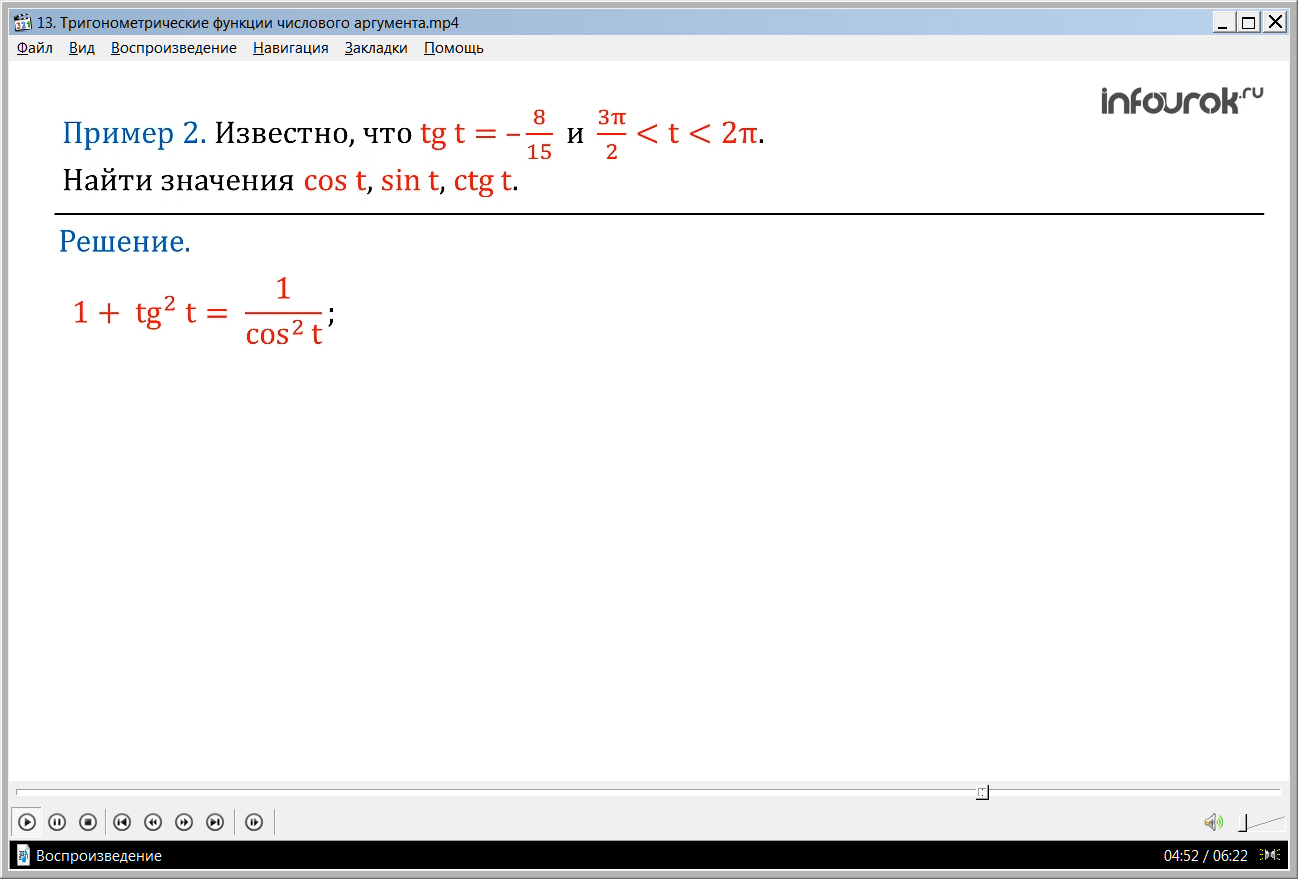
ПРИМЕР 2. Известно, что tgt = – и < t < 2π( тангенс тэ равен минус восемь пятнадцатых и тэ принадлежит промежутку от трех пи на два до двух пи). Найти значения cost, sint, ctgt.
Решение. Воспользуемся данным соотношением , подставив значение в эту формулу получим:
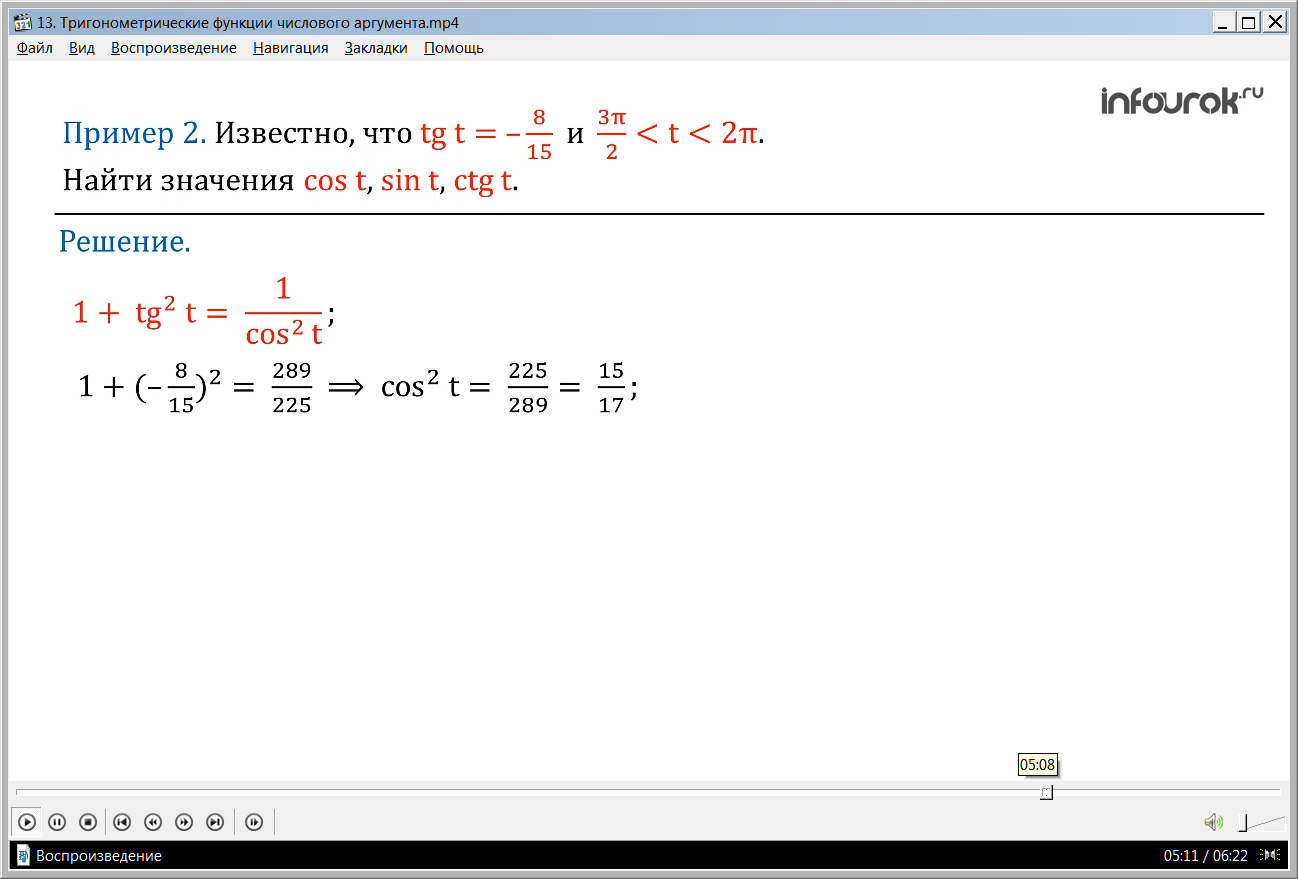
= 1 + (– )2 = ( единица на косинус квадрат тэ равно сумме единицы и квадрата минус восьми пятнадцатых). Отсюда находим cos2 t =
( косинус квадрат тэ равен двести двадцать пять двести восемьдесят девятых). Значит, cost = (косинус тэ равен пятнадцать семнадцатых) или
cost = . По условию аргумент t принадлежит четвертой четверти, где cost>0. Поэтому cost = .(косенус тэ равен пятнадцать семнадцатых)
Найдем значение аргумента синус тэ. Так как из соотношения (показать соотношение tgt = при t ≠ + πk, kϵZ) синус тэ равен произведению тангенса тэ на косинус тэ, то подставив значение аргумента тэ ..тангенс тэ равен минус восемь пятнадцатых.. по условию, а косинус тэ равен из решенного ранее, получаем
sint = tgt ∙ cost = (- ) ∙ = – , (синус тэ равен минус восемь семнадцатых)
ctgt = = - . (так как котангенс тэ, есть величина обратная тангенсу, значит, котангенс тэ равен минус пятнадцать восемнадцатых)
| Автор | |
|---|---|
| Дата добавления | 27.07.2014 |
| Раздел | Алгебра |
| Подраздел | Видеоурок |
| Просмотров | 8591 |
| Номер материала | 836 |