
Урок "Применение производной для исследования функций на монотонность"

Краткое описание документа:
Видеоурок «Применение производной в исследовании функций на монотонность» демонстрирует наглядный материал для урока алгебры. В ходе урока вводится понятие монотонности, демонстрируются важные теоремы, используемые в решении задач, примеры решения заданий. С помощью видеоурока учитель может повысить эффективность обучения. Демонстрация материала может заменить объяснение учителя или послужить наглядным пособием для сопровождения объяснения учителя.
Наглядность материала обеспечивается вставкой рисунков, на которых изображаются графики, использованием анимации, позволяющей подать материал в более удобном виде для восприятия. Использование анимации и различных цветов при составлении видео помогает концентрировать внимание учеников, способствует лучшему запоминанию и пониманию темы.
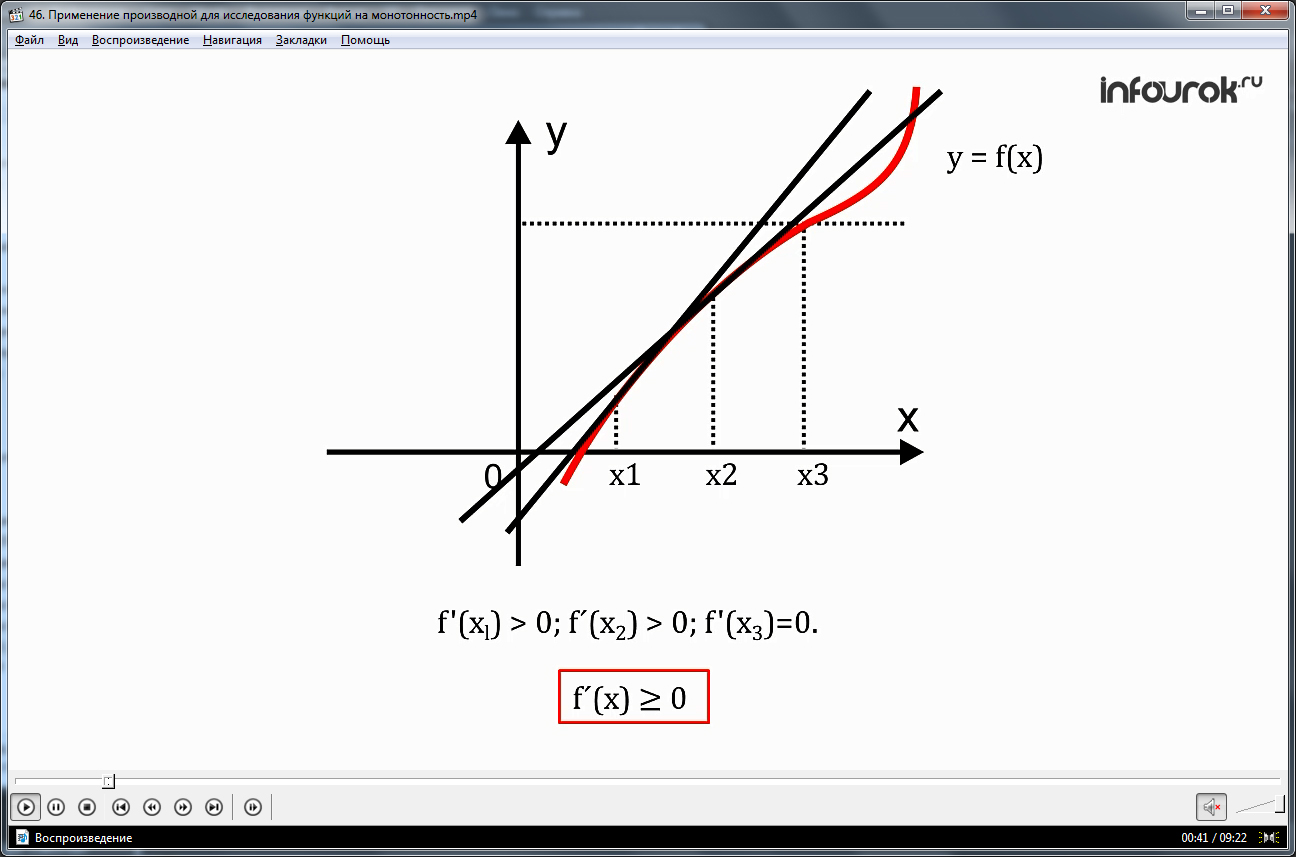
Демонстрация видеоурока начинается с представления темы урока и изображения графика y=f(x), возрастающей на числовой оси. В некоторых двух точках х1 и х2 к графику функции проводятся касательные. Отмечается, что так как касательные образуют с осью Х острый угол, они имеют положительный угловой коэффициент. Зная, что угловой коэффициент определяется производной функции в точке, для данных касательных отмечается f΄(x1)>0 и f΄(x2)>0. Рассматривая касательную в точке x3, нужно отметить ее параллельность оси Х, то есть f΄(x3)=0. Делается вывод о том, что для любой дифференцируемой непрерывной возрастающей функции в любой ее точке f΄(x)>=0.
Далее рассматривается функция y=f(x), с убывающими значениями при движении по числовой оси Х. К трем точкам графика функции проведены касательные. Эти касательные составляют с прямой Х тупые углы, то есть угловой коэффициент касательных - отрицательное число, то есть f΄(x1)<0 и f΄(x2)<0, f΄(x3)<0. Это значит, что производная дифференцируемой убывающей функции - отрицательное число или нуль f΄(x) <=0. Также озвучивается общий вывод из рассмотренных свойств производной. Указывается, для убывающей (возрастающей) на некотором открытом промежутке дифференцируемой функции характерно наличие неположительной (неотрицательной) производной в каждой точке. Также справедливо обратное утверждение об убывании (возрастании) функции, с неположительной (неотрицательной) производной на всем промежутке.
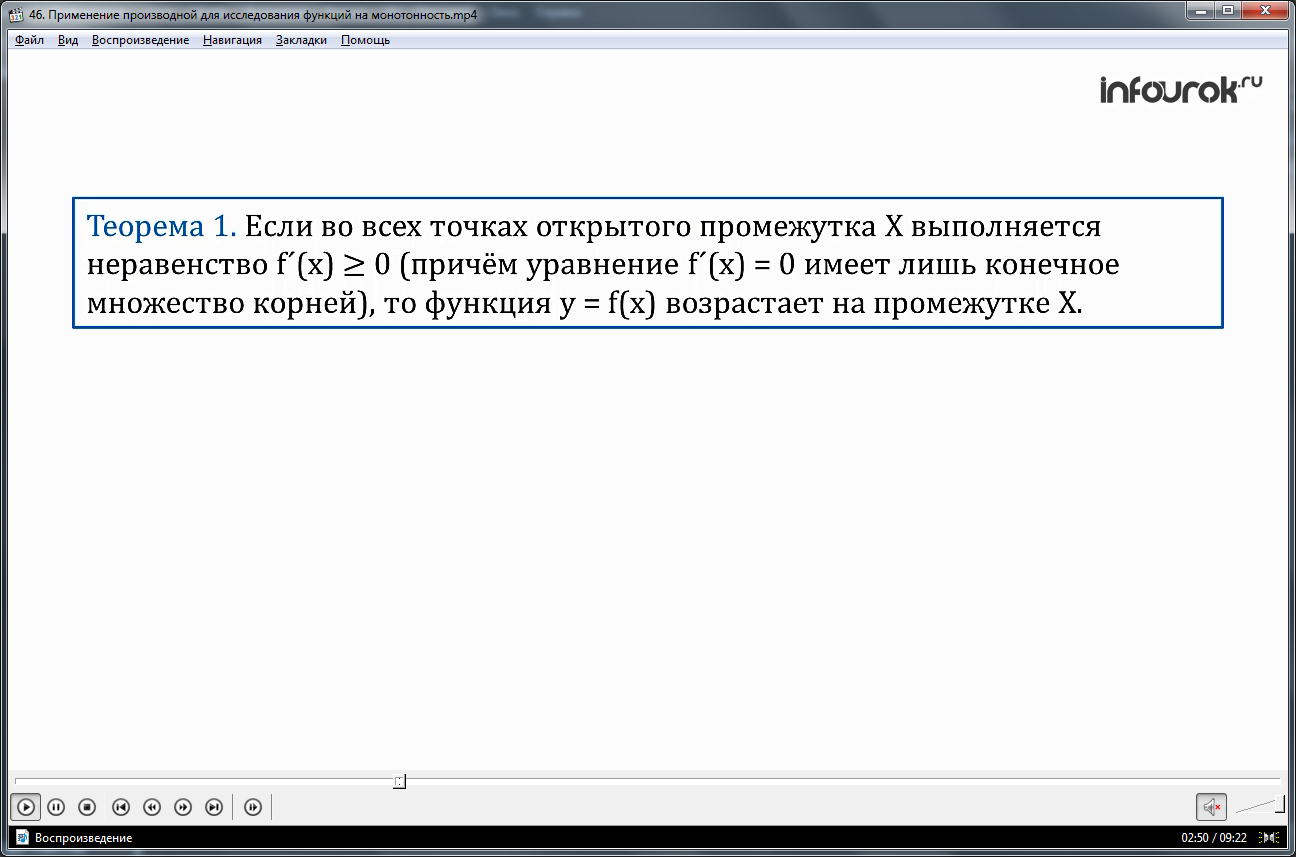
Далее предлагается рассмотреть теоремы, подтверждающие рассмотренные свойства функций. В теореме 1 указано, при справедливости для открытого промежутка неравенства f΄(x)>=0, а уравнение f΄(x)=0 имеет конечное множество корней, то y=f(x) – возрастающая. Вторая теорема утверждается, что при справедливости для открытого промежутка справедливо f΄(x) <=0, а уравнение f΄(x)=0 имеет конечное множество корней, то y=f(x) – убывающая.
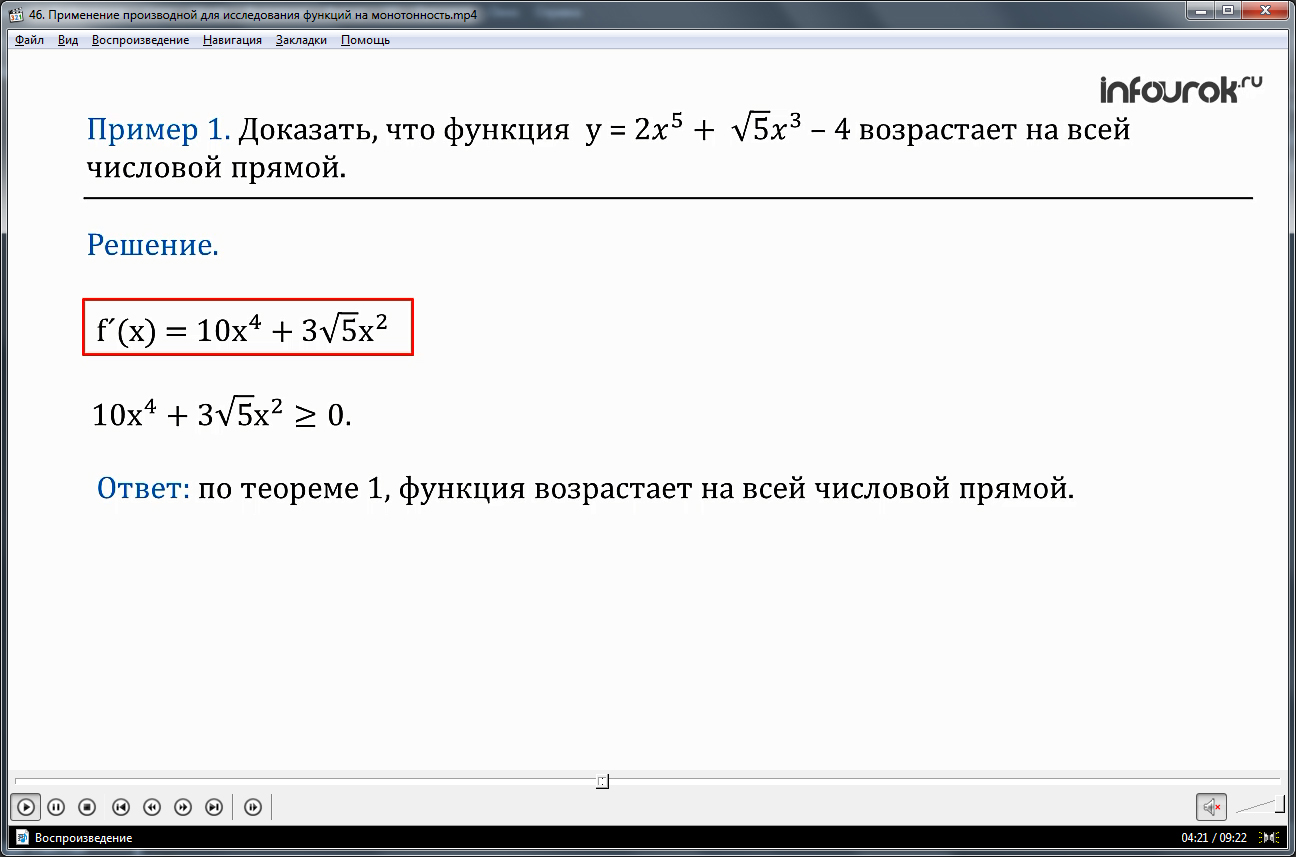
Рассматривается пример, в котором доказывается возрастание на числовой прямой функции у=2х5+√5х3-4. Сначала определяется производная данной функции. Это будет f΄(x)= 10х4+3√5х2. Очевидно, что на числовой прямой данное выражение принимает положительные значения 10х4+3√5х2>=0. Так как f΄(x) >=0, то согласно первой теореме, по числовой прямой функция возрастает.
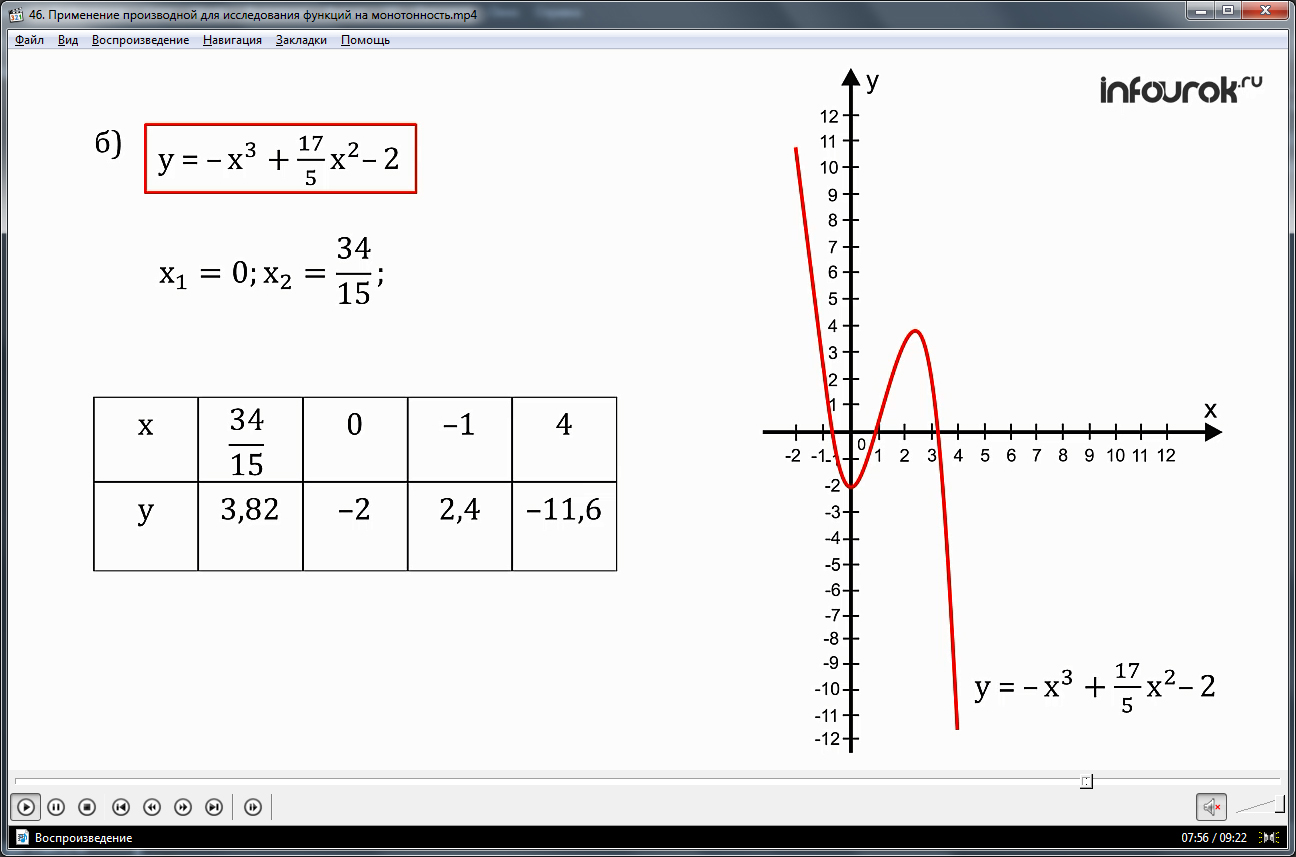
Во втором примере необходимо исследовать функцию -х3+(17/5)х2-2 на монотонность, а также построить ее график. Ученикам выводится напоминание о том, как проводится исследование на монотонность. Отмечается, что исследование на монотонность значит, нахождение промежутков возрастания, убывания функции. Поэтому нужно определить знак производной. Находим f΄(x) =-3х2+(34/5)х. После выведения за скобки постоянного множителя х корни f΄(x) =0 найти легко. Найденные значения х1=0 и х2=34/15. Данные точки образуют промежутки, на которых может меняться знак производной и меняться направление – возрастание или убывание функции. На рисунке изображается числовая прямая, на которой отмечены найденные точки х1=0 и х2=34/15. Отмечается, что на промежутке (-∞;0) производная отрицательная, а на промежутке (0;34/15) производная положительная, на последнем промежутке (34/15;+∞) производная отрицательная. В результате исследования можно сделать вывод, что на первом и последнем промежутке (-∞;0] и [34/15;+∞) функция возрастает, а на втором [0;34/15] убывает.
Чтобы выполнить построение графика функции, предлагается составить соответствующую таблицу, в которую входят координаты особых точек и несколько других точек. Зная сведения о промежутках возрастания и убывания функции и значения ее точек, можно строить график. Отмечается, что при построении графика также учитывается непрерывность функции и то, что в особых точках х1=0 и х2=34/15 касательная к графику параллельна оси абсцисс. На рисунке рядом с функцией строится график.
Дополнительно рассматривается случай, когда производная функции на всей области определения равна нулю. Очевидно, это означает, что она не будет убывающей или возрастающей. Отмечается, что такое поведение характерно для постоянной функции y=С. Без доказательства представляется теорема 3, в которой указано, что если для всех точек промежутка Х f΄(x)=0, то функция y=f(x) – постоянная на Х.
В примере 3 рассматривается доказательство тождества sin2x+cos2x=1. Принимая за функцию f(x)= sin2x+cos2x, находим ее производную f΄(x)=( sin2x+cos2x)΄. Применив свойство производной суммы, находим, что f΄(x)=0. Если производная равна нулю, то f(x)=С. Можно найти постоянную С, подставив значение – для х=0 значение функции f(0)= sin20+cos20=1, значит, С=1.
Видеоурок «Применение производной для исследования функций на монотонность» рекомендуется применять на традиционном школьном уроке как наглядный материал. Также пособие может быть полезно учителю, осуществляющему дистанционное обучение. При необходимости углубить понимание учеником данной темы, материал может быть предложен для самостоятельного рассмотрения.
ТЕКСТОВАЯ РАСШИФРОВКА:
Рассмотрим график некоторой возрастающей дифференцируемой функции
у = f(x) (игрек равен эф от икс) и проведем касательные к этому графику в некоторых фиксированных точках х = х1, и х = х2.(икс равен икс один, и икс два). Видим, что они составляют с осью х острый угол, а значит, у обеих прямых положительный угловой коэффициент. Но по определению угловой коэффициент касательной равен значению производной в абсциссе точки касания. Следовательно, f '(xl) >0 и f ´(x2) >0. (эф штрих от икс первого больше нуля) (эф штрих от икс второго больше нуля). А в точке х =х3 касательная параллельна оси х, то есть в этой точке выполняется равенство
f '(x3)=0. Получаем в любой точке х из области определения возрастающей дифференцируемой функции выполняется неравенство f ´(x)0 (эф штрих от икс больше или равен нулю).
Сейчас рассмотрим график некоторой убывающей дифференцируемой функции y = f(x) и проведем касательные к графику в точках x=x1 и х=х2.
( икс равен икс один, и икс два). Видим, что они составляют с осью х тупой угол, а значит, имеют отрицательный угловой коэффициент. А так как угловой коэффициент касательной равен значению производной в абсциссе точки касания, то имеем, f ´(х1) < 0 и f ´(x2) < 0(эф штрих от икс первого меньше нуля) (эф штрих от икс второго меньше нуля). А в точке х=х3 касательная параллельна оси х, а, значит, выполняется равенство f ′(x3) =0. Таким образом, в любой точке х из области определения убывающей дифференцируемой функции выполняется неравенство f ´(x)0(эф штрих от икс меньше или равен нулю).
Данная связь возрастания и убывания функции и знаков производной к ней на некотором открытом промежутке двухсторонняя: если функция возрастает (убывает) на промежутке и имеет на нем производную, то производная неотрицательна (неположительная); и наоборот если производная функции неотрицательна (неположительная), то функция возрастает (убывает) на промежутке.
Сформулируем данные утверждения в виде теорем.
Теорема 1. Если во всех точках открытого промежутка X выполняется неравенство f'(x)0 (причем уравнение f´(x) = 0 имеет лишь конечное множество корней), то функция y=f(x) возрастает на промежутке X.
Теорема 2. Если во всех точках открытого промежутка X выполняется неравенство f'(x)0 (причем уравнение f'(x)=0 имеет лишь конечное множество корней), то функция y=f(x) убывает на промежутке X.
Пример 1. Доказать, что функция у =2х5 + х3 –4 возрастает на всей числовой прямой.
Решение. Найдем производную заданной функции: f´(х)= 10х4 + 3х2.( эф штрих равен сумме десяти икс в четвертой степени и три корня из пяти икс в квадрате).
Так как, производная функции представляет собой сумму переменных в четных степенях и коэффициенты при х положительны, то при любом х из области определения, очевидно, что выполняется неравенство
10х4 + 3х20. Значит, по теореме 1, функция возрастает на всей числовой прямой.
Пример 2. Исследовать на монотонность и построить график функции
у = –х3 +х2 –2.
Решение. Исследовать функцию на монотонность — это значит выяснить, на каких промежутках области определения функция возрастает, а на каких убывает. Согласно теоремам 1 и 2 это связано со знаком производной.
Найдем производную данной функции: f'(х)= –3х2+х и далее
f'(х)=–х(3x–), получаем производная равна нулю в точках х1=0 и х2=
На рис. 1 схематически указаны знаки производной по промежуткам области определения и поведение функции на каждом из промежутков:
на луче (–,0) производная отрицательна, на интервале (0, ) (от нуля до тридцати четырех пятнадцатых)— положительна, на луче (; +) (от тридцати четырех пятнадцатых до плюс бесконечности)— отрицательна. Значит, на первом из указанных промежутков функция убывает, на втором возрастает, на третьем убывает.
Обычно, если функция непрерывна не только на открытом промежутке, но и в его концевых точках, эти концевые точки включают в промежуток монотонности функции.
Таким образом, заданная функция убывает на лучах (–, 0] и [, +), возрастает на отрезке [0; ].
Графики функций строят «по точкам». Для этого надо составить таблицу значений функции у= –х3 +х2 –2, куда обязательно следует включить значения функции в концевых точках промежутков монотонности х = 0 и
х = и еще пару-тройку значений:
Отметим эти точки на координатной плоскости. Учтем найденные в промежутки возрастания и убывания функции, а также то, что в точках х = 0 и х = производная функции равна нулю, т.е. касательная к графику функции в указанных точках параллельна оси абсцисс. Учтем, наконец, то, что функция непрерывна, т.е. ее графиком является сплошная линия. График заданной в условии функции изображен на рис. 2.
Завершая рассуждения по исследованию функций на монотонность, обратим внимание на одно обстоятельство. Мы видели, что если на промежутке X выполняется неравенство f'(x)>0, то функция y = f(x) возрастает на промежутке X, если же на промежутке X выполняется неравенство f ′(x) < 0, то функция убывает на этом промежутке. А что будет, если на всем промежутке выполняется тождество f'(x) =0 ? Видимо, функция не должна ни возрастать, ни убывать. Что же это за функция? Ответ очевиден – это постоянная функция у = С (буква С — первая буква слова constanta, что означает «постоянная»). Справедлива следующая теорема, формальное доказательство которой мы не приводим, ограничиваясь приведенными выше правдоподобными рассуждениями.
Теорема 3. Если во всех точках открытого промежутка X выполняется равенство f´(х) = 0, то функция у = f(x) постоянна на промежутке X.
Пример 3. Докажем тождество sin2x+cos2x = l.
Рассмотрим функцию у = f(x), где f(x) = sin2x+cos2 х.
Найдем ее производную:
f´(x) =(sin2x +cos2 х)' =(sinxsinx)'+(cosxcosx)' = (cosxsinx+sinxcosx)+
+(–sinx cosx + cosx (–sinx))= 2sin x cos x–2 sin x cos x=0.
Итак, для всех х выполняется равенство f'(x)=0, значит, функция f(x) является постоянной, т.е. f(x)=C.
Чтобы найти значение постоянной С, достаточно вычислить значение функции в любой точке х, например, х = 0. Имеем: f(0) = sin2 0+cos2 0=0+1=1.
Таким образом, С = 1, т. е. sin2x+cos2x = 1.
| Автор | |
|---|---|
| Дата добавления | 27.07.2014 |
| Раздел | Алгебра |
| Подраздел | Видеоурок |
| Просмотров | 5711 |
| Номер материала | 869 |