
Презентация "Предел числовой последовательности. Свойства сходящихся последовательностей"

Краткое описание документа:
Презентация «Предел числовой последовательности» - наглядное пособие для проведения урока алгебры по данной теме. В ходе презентации рассматриваются свойства сходящихся последовательностей, вычисление пределов последовательностей и суммы бесконечной геометрической прогрессии. С помощью презентации учитель может наглядно представить учебный материал, улучшить понимание предмета и запоминание формул и свойств учениками, формировать умение решать задания с использованием изученного теоретического материала.


Представление информации в форме презентации предоставляет учителю дополнительные преимущества, способствующие повышению эффективности занятий. Анимационные эффекты помогают наглядно представить материал, подавая его последовательно и структурировано. Также использование анимации – один из способов удержания внимания учеников на изучении предмета. Демонстрация содержит рисунки, для представления которых учителю потребовалось бы дополнительные пособия. Изучаемые понятия можно выделить цветом, способствуя их запоминанию.
Презентация начинается с представления свойств числовой последовательности. В первом свойстве отмечается единственность предела, к которому сходится последовательность. Во втором свойстве указано, что последовательность ограничена, если она сходится. Также указанное свойство дополнено замечанием, что при ограниченности последовательности она обязательно будет сходящейся. Примером служит последовательность -1, -2, -3, -1, -2, -3, … очевидно, что последовательность имеет обе границы, однако не является сходящейся.
На втором слайде представлено третье свойство последовательности, в котором отмечается, что монотонная и ограниченная последовательность будет сходиться. Также на слайде представлен портрет математика, автора формулировки теоремы Карла Вейерштрасса. Проследить рассмотренные свойства можно на примерах, которые представлены на слайде 3, где демонстрируется нахождение пределов трех последовательностей (1) lim1/n=0 при n→∞, (2) limqn=0 при n→∞ для |q|<1, (3) lim С=С при n→∞.
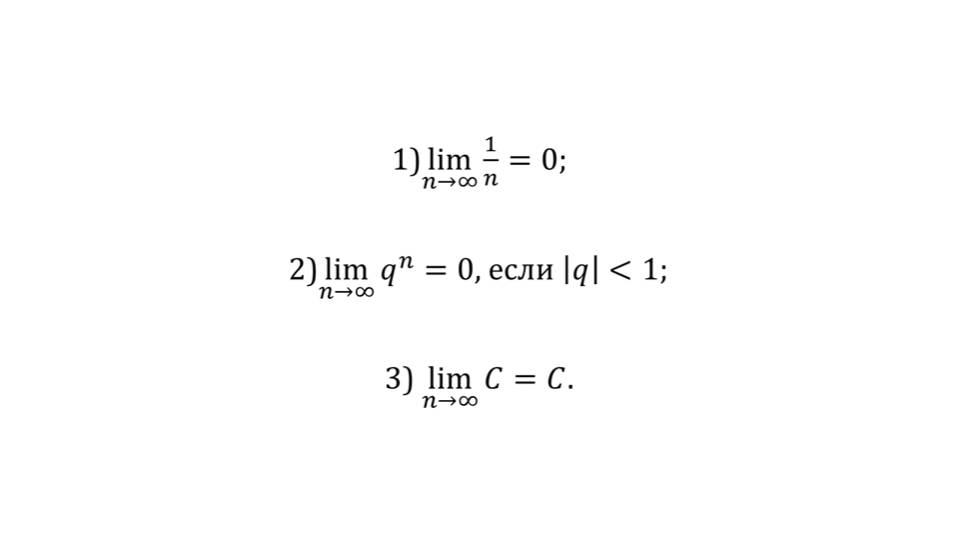

На слайде 4 демонстрируется теорема о свойствах сходящихся последовательностей. Отмечается, что если есть пределы последовательностей limxn=b при n→∞ blimyn=с при n→∞, то (1) при вычислении предела суммы последовательностей необходимо сложить пределы каждой их них (2) lim (xn+ yn) = b+с, при n→∞ (2) предел произведения двух последовательностей определяется произведением пределов каждой из них lim (xnyn) = bс при n→∞, (3) для вычисления предела частного двух последовательностей нужно найти отношение пределов каждой из них lim (xn/yn) = b/с при n→∞, (4) предел последовательности, имеющей постоянный множитель, при вычислении предела множитель выносится lim (kxn) = kbпри n→∞ для некоторого ненулевого k.


Усвоить изученный материал помогает ряд примеров, рассмотренных на слайде 5. Для поиска предела последовательности sn=1/n2 она представляется в виде произведения двух последовательностей (1/n)·(1/n). Так как предел каждой из них при n→∞ равен 0, то предел lim1/n2 = 0. Аналогично определяется lim1/n4 = 0. Для вычисления предела последовательности k/n6 множитель k выносится за скобки. Но так как пределом последовательности является 0, то и произведение будет 0. Для запоминания представлено нахождение предела подобной последовательности в общем виде limk/nm = 0 при n→∞. В последнем примере нужно вычислить предел последовательности, состоящей из суммы. Разбивая предел суммы на сумму пределов, получаем возможность более просто вычислить предел lim (14/n4+√28/ n7-7/9)=7/9 при n→∞.
В примере 2 на слайде 6 необходимо вычислить limSn при n→∞ для последовательности, где Sn=b1(qn-1)/(q-1), а также известно, что b1≠0 и |q|<1. Зная изученные свойства пределов, можно вынести на знак предела множитель b1/(q-1). После этого получим limb1(qn-1)/(q-1)= b1/(q-1)lim(qn-1). Так как lim(qn-1)=0-1=-1, то значение предела последовательности limb1(qn-1)/(q-1)= b1/(1-q) при n→∞.
Пример 3 описывается вычисление предела последовательности (√3·n5-17)/( n5+9). Для вычисления предела рекомендуется почленно разделить числитель и знаменатель дроби на высшую степень переменной. После проведения вычислений получаем при n→∞ lim (√3-17/ n5)/(1+9/ n5). Применяя свойство о пределе частного, отмечаем, что предел числителя √3, а знаменатель стремится к 1, поэтому пределом последовательности будет при n→∞ lim(√3·n5-17)/( n5+9)=√3.

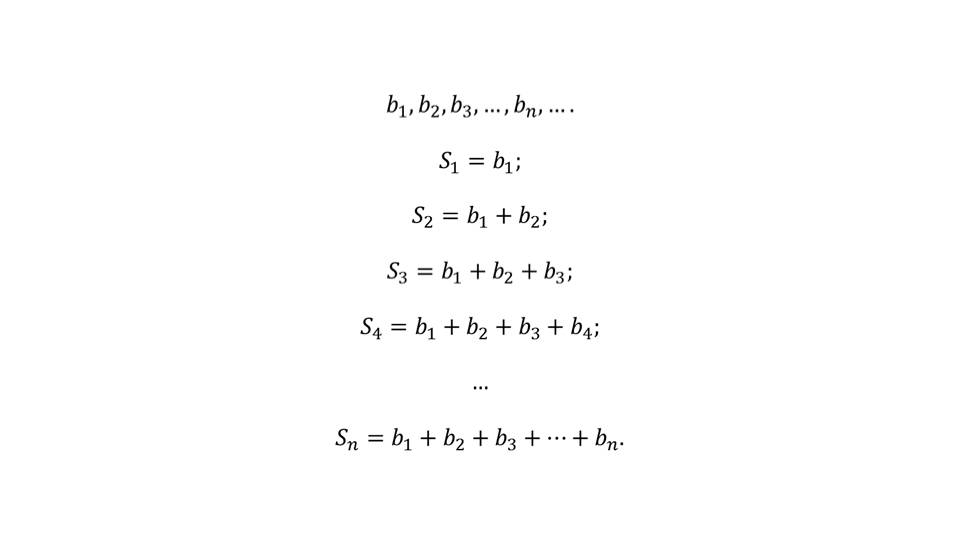
Далее рассматривается пример последовательности Sn, каждый член которой формируется как сумма членов последовательности bn. При этом S1= b1, S2= b1+ b2, S3= b1+ b2+ b3 и т.д. таким образом формируется последовательность S1 , S2 , S3, … Отмечается, что последовательность может сходиться и расходиться. При сходящейся последовательности Sn к некоторому числу S, данное число называют суммой геометрической прогрессии. В случае расходящейся последовательности о сумме прогрессии не говорят. В рамку для запоминания выделен случай, когда для |q|<1 сумма прогрессии, где Sn= b1+ b2+b3+…+ bnопределяется по формуле Sn=b1/(1-q).
На слайде 11 рассматривается пример, в котором нужно найти сумму геометрической прогрессии 12, 6, 3, 3/2, ¾,… Используя рассмотренную выше формулу, определяем ее элементы - b1=12, q=1/2. Так как q меньше единицы, сумма определяется по формуле Sn=b1/(1-q). При подстановке значений и вычисления получаем S=24.
На примере 5 описывается нахождение члена геометрической прогрессии по известной сумме ее членов S=18и сумме квадратов ее членов 64,8. Чтобы решить задание, сначала прогрессия представляется как b1, b2, b3… со знаменателем q. Сумма членов такой прогрессии вычисляется по формуле Sn=b1/(1-q). Для последовательности квадратов b12, b22, b32… со знаменателем q2 сумма членов вычисляется по формуле Sn=b12/(1-q2). Таким образом для определения первого члена прогрессии и знаменателя следует решить систему уравнений b1/(1-q)=18 и b12/(1-q2)=64,8. Выразив из одного уравнения b1, подставим выражение в другое уравнение, решив систему методом подстановки. В результате вычислений получим q=2/3, а b1=6. Зная эти параметры, по формуле b3= b1q2 получаем b3=8/3. Решение найдено.

Презентация «Предел числовой последовательности» предназначена для использования в ходе традиционного урока алгебры в школе. Материал может успешно применяться учителями, осуществляющими дистанционное обучение. Также пособие может быть рекомендовано для самостоятельного изучения ученикам, требующих дополнительных занятий для улучшения понимания предмета.
| Автор | |
|---|---|
| Дата добавления | 27.07.2014 |
| Раздел | Алгебра |
| Подраздел | Презентация |
| Просмотров | 4022 |
| Номер материала | 816 |