
Презентация "Аксиомы стереометрии"

Краткое описание документа:
Как и планиметрия, стереометрия держится на некоторых аксиомах, на основе которых в дальнейшем будут доказываться теоремы и решаться задачи. Аксиомы, как известно, не требуют доказательств. Если пропустить данную тему, то дальнейшее изучение стереометрии не будет иметь никакого смысла. Решения станут непонятны, ученик отстанет от своих сверстников, успеваемость во многом понизиться. Поэтому стоит хорошо изучить данную презентацию. Сделать это можно и в классе вместе с учителем, и в домашней обстановке. Упустив эту тему, дальнейшие решения в последующих презентациях не будут понятны, ведь ссылаются на аксиомы в данном уроке.


Презентация состоит из 14 слайдов, на первом из которых напоминается определение понятия аксиомы. Далее уточняется, что же является аксиомой в стереометрии. Первая аксиома в данном разделе говорит о том, что через три точки можно провести лишь одну плоскость. Это очень важное утверждение. Школьники должны хорошо себе это представлять и понимать, что через одну или две точки можно провести бесконечное множество плоскостей. Изображение плоскости, проведенной через три точки, приводится на этом же слайде.

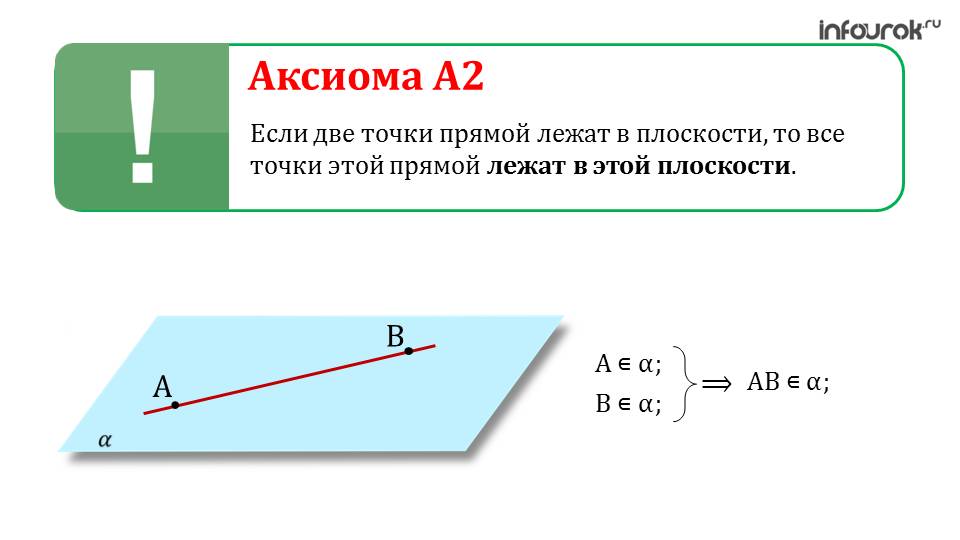
Вторая аксиома гласит о том, что если некоторые точки произвольной прямой (минимум 2) лежат на плоскости, то все бесконечное количество точек также лежат на этой плоскости. Убедиться в этом можно также просто. Однако доказать нельзя. На то утверждение и является аксиомой. Если ученики не понимают или не представляют ту или иную аксиому, можно предложить им доказать обратное практическим образом. То есть привести хоть один пример, который будет опровергать утверждение. Благодаря этому они смогут развить математическое и пространственное мышление.
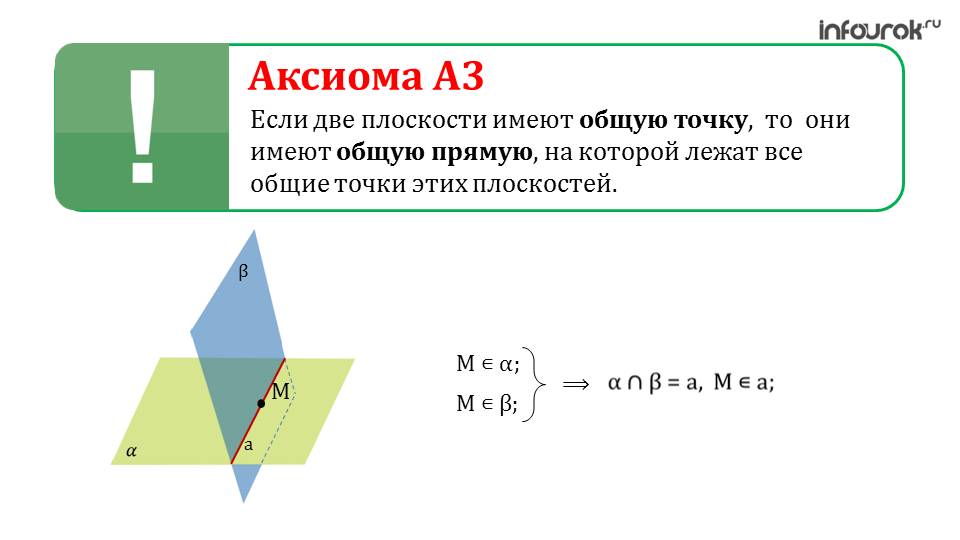
Следующая аксиома, А3, говорит о пересечении двух плоскостей об общей прямой, которой они обладают. Плоскости изображены через параллелограммы. Есть также иные способы их обозначения, однако данный является наиболее распространенным во многих учебниках, в том числе и школьных.
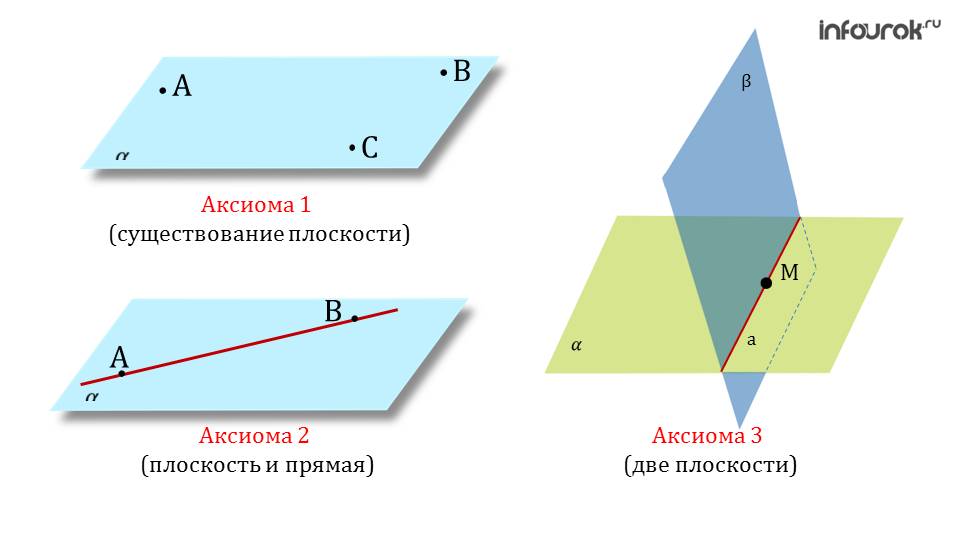
На следующем слайде выводятся изображения трех аксиом. Все эти чертежи желательно перечертить в тетрадях, чтобы лучше запомнить и понять. Таким образом, можно лучше запомнить аксиомы. Итак, были рассмотрены три основных утверждения, к которым школьники неоднократно будут возвращаться. Желательно знать их формулировки и уметь правильно ими воспользоваться, также воспроизвести их в случае необходимости.
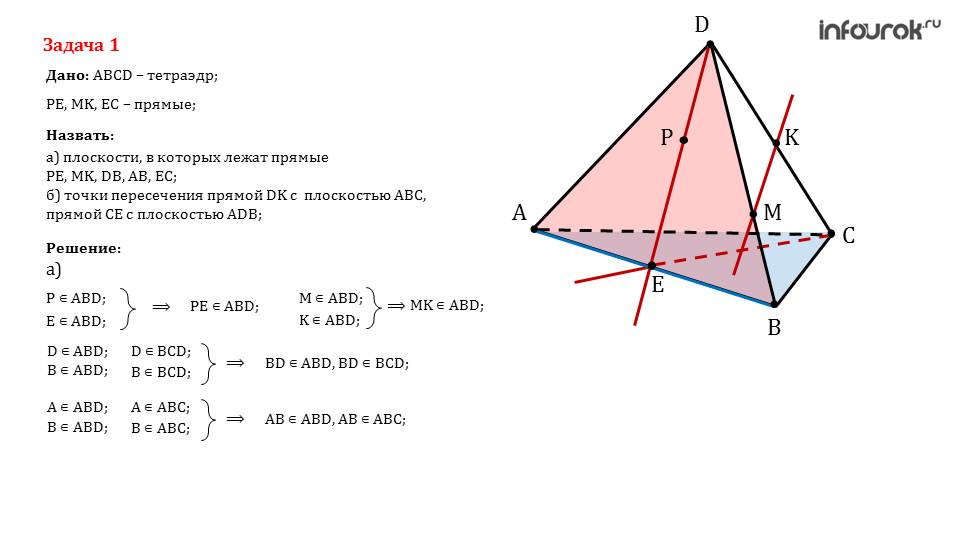
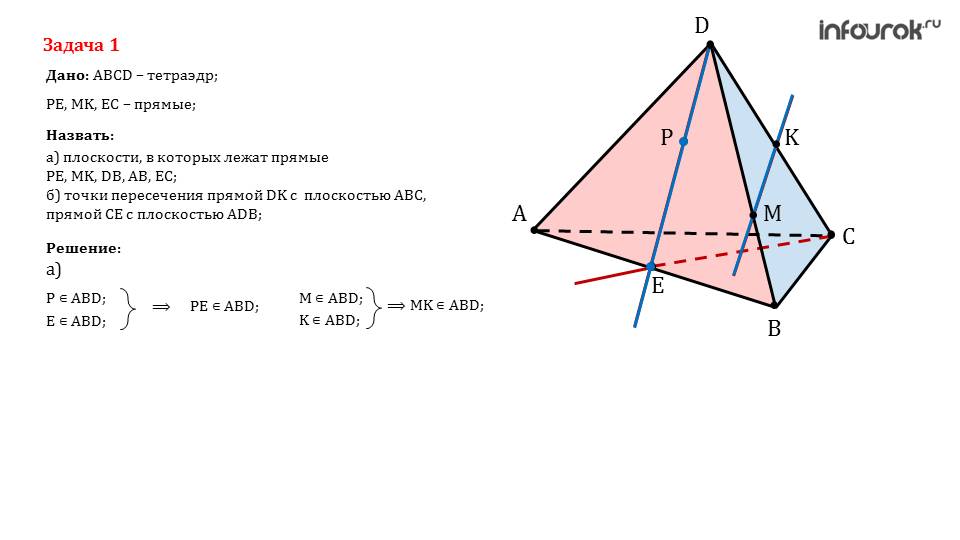
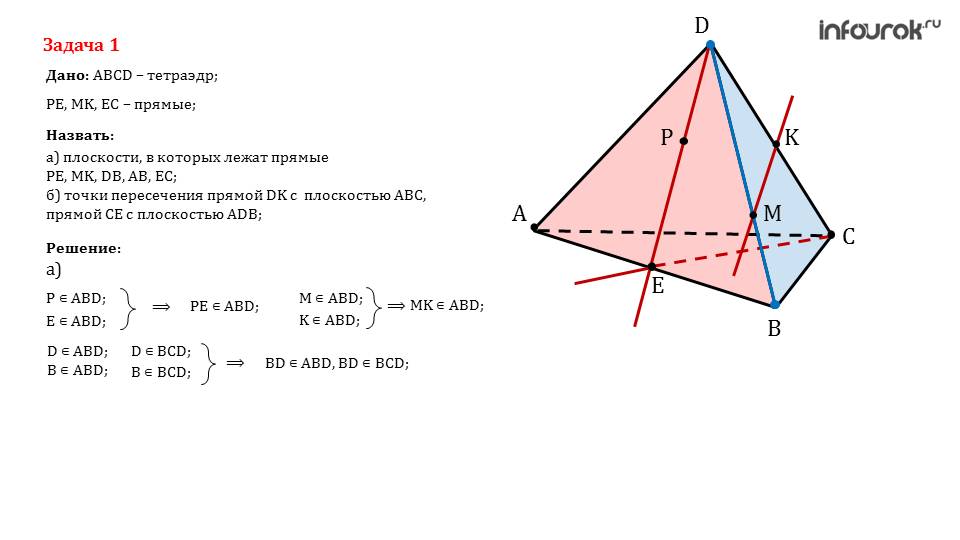
Далее презентация предлагает рассмотреть задачу, в которой исследуется такое тело, как тетраэдр. С этой фигурой школьники ранее были знакомы, и вероятнее всего имели дело. Для того, чтобы учитель понял, могут ли справиться ученики с пространственным мышлением, предлагается определить некоторые плоскости, точки пересечения и т.д. на фоне этой фигуры. Если у некоторых возникают трудности, то стоит им задать на дом похожие примеры, чтобы они смогли лучше понять суть.
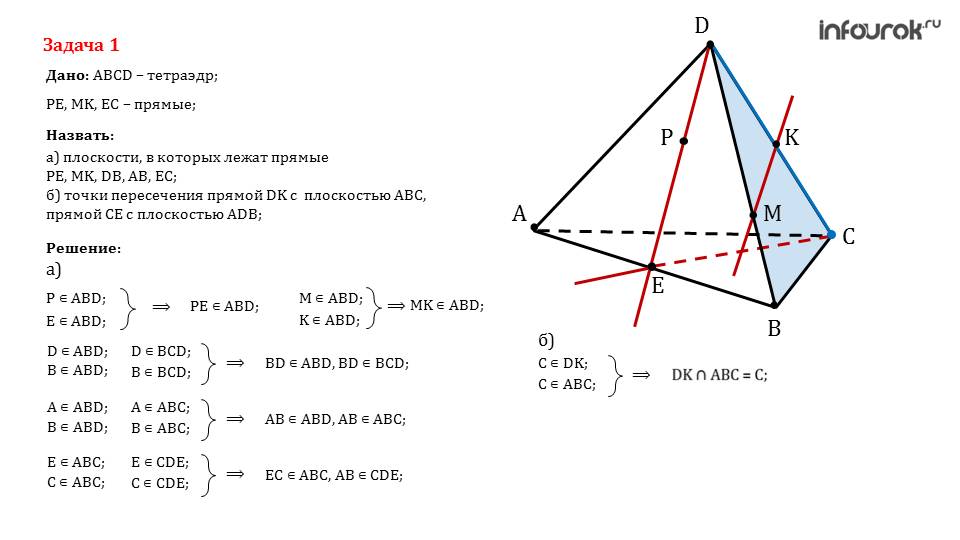
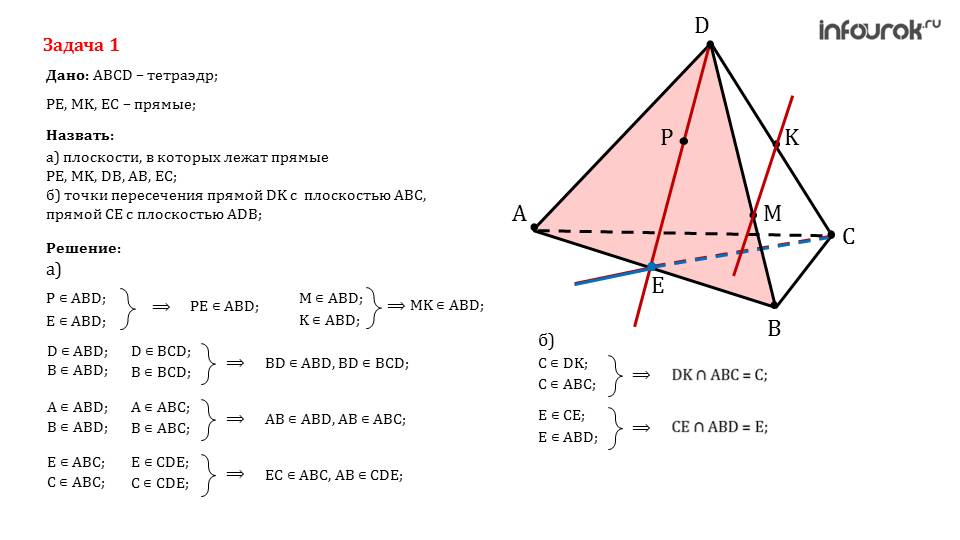
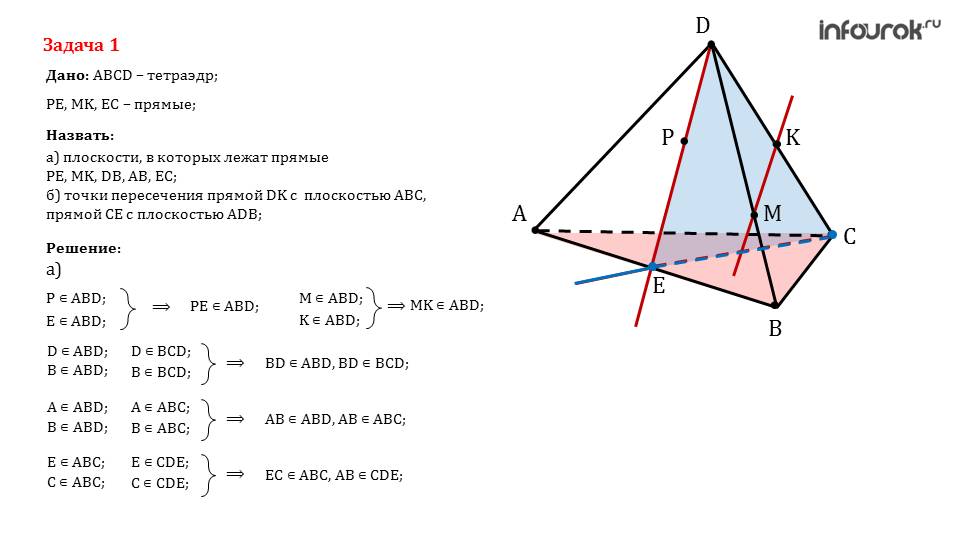
После этой задачи приводится еще одна. Для ее решения, необходимо вспомнить все изученные аксиомы и научиться ими воспользоваться. В случае, если останется время от урока, стоит рассмотреть как можно больше практических задач с классом.
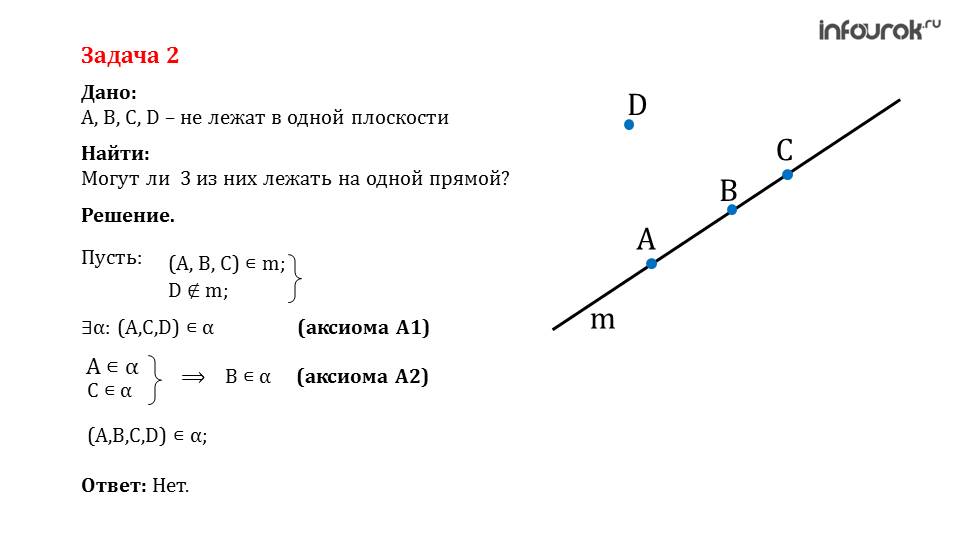
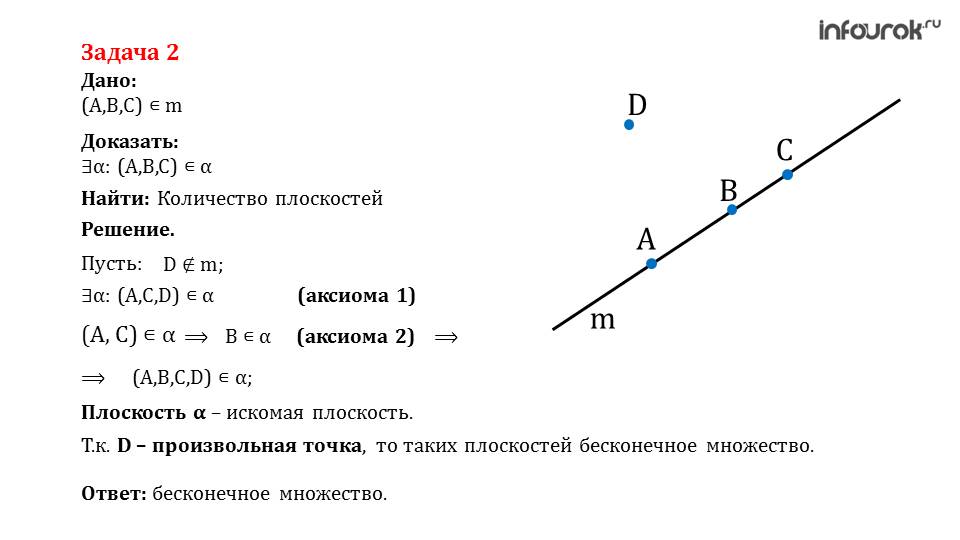
С помощью презентации «Аксиомы стереометрии» молодой учитель может провести интересный урок, привлечь внимание учеников. Благодаря оптическому восприятию, школьники смогут лучше усвоить и понять материал. При написании плана конспекта, которым занимаются в обязательном порядке молодые учителя, презентация также пригодится. Она поможет правильно структурировать урок и не пропустить ни одну аксиому, ни одно важное объяснение и замечание.
Примеры, которые приводятся в презентации, также станут полезны при проведении урока.
| Автор | |
|---|---|
| Дата добавления | 28.10.2014 |
| Раздел | Геометрия |
| Подраздел | Презентация |
| Просмотров | 3354 |
| Номер материала | 874 |