19.09.2017
1324
0
Бесплатно
Уроки математики / Презентация / Презентация "Алгебра Жегалкина" по дисциплине "Элементы математической логики"
Презентация "Алгебра Жегалкина" по дисциплине "Элементы математической логики"
1
из 10
Описание презентации по отдельным слайдам:
№ слайда 1
Алгебра Жегалкина Беляева Татьяна Юрьевна ГБПОУ КК «Армавирский машиностроительный техникум» Преподаватель математических дисциплин
№ слайда 2
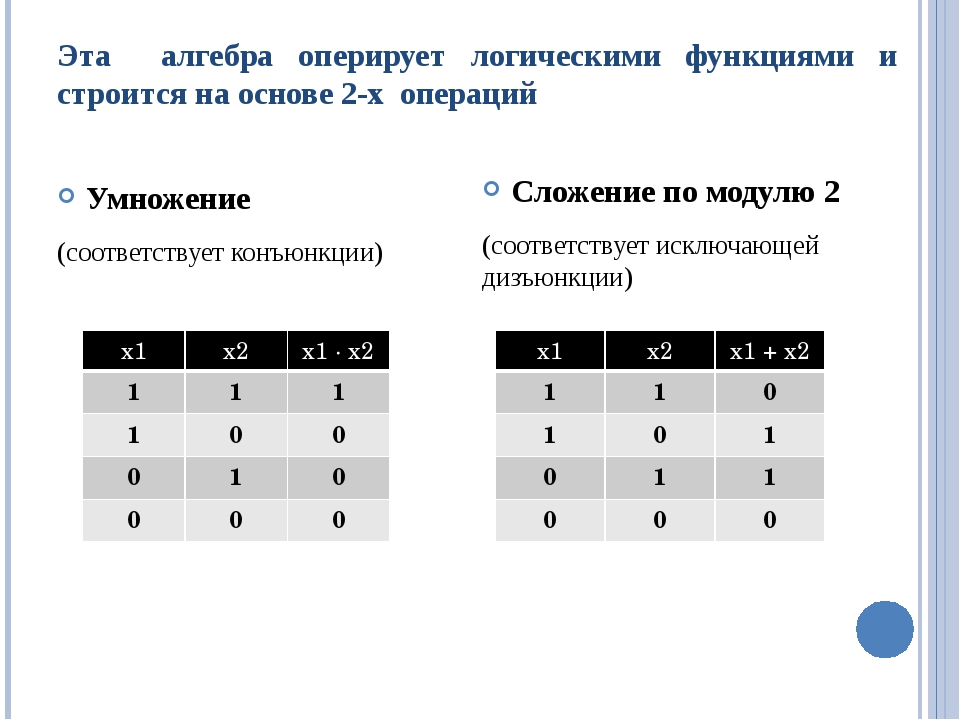
Эта алгебра оперирует логическими функциями и строится на основе 2-х операций Умножение (соответствует конъюнкции) Сложение по модулю 2 (соответствует исключающей дизъюнкции) х1 х2 х1 ∙ х2 1 1 1 1 0 0 0 1 0 0 0 0 х1 х2 х1 + х2 1 1 0 1 0 1 0 1 1 0 0 0
№ слайда 3
1. Свойства алгебры Жегалкина 1. Коммутативность х1 ∙ х2 = х2 ∙ х1 х1 + х2 = х2 + х1 2. Ассоциативность (х1 ∙ х2) ∙ х3 = х1 ∙ (х2 ∙ х3) (х1 + х2) + х3 = х1 + (х2 + х3) 3. Дистрибутивность умножения относительно сложения х1 ∙ (х2 + х3) = х1 ∙ х2 + х1 ∙ х3 (!!) Второй дистрибутивности нет
№ слайда 4
1. Свойства алгебры Жегалкина 4. Свойства констант х ∙ 0 = 0 х ∙ 1 = х х + 0 = х 5. Закон приведения подобных х + х = 0 6. Закон поглощения для умножения х ∙ х = х (!!) Свойства 1-4 полностью соответствуют свойствам алгебры чисел
№ слайда 5
2. Соотношения, устанавливающие связь булевой алгебры с алгеброй Жегалкина х = 1 + х x1 /\ x2 = x1 ∙ x2 x1 \/ x2 = x1 + x2 + x1 ∙ x2 ___________________________________ x1 ∙ x2 = x1 /\ x2 x1 + x2 = x1 /\ x2 \/ x1 /\ x2 (!!) Все эти формулы легко доказываются с помощью таблиц истинности
№ слайда 6
3. Многочлены Жегалкина Каноническим многочленом Жегалкина называется такой многочлен, все члены которого не содержат числовых коэффициентов, отличных от 1, и линейны относительно любой из переменных (все переменные в 1-ой степени) (!!) Любую булеву функцию можно единственным образом представить в виде многочлена Жегалкина
№ слайда 7
ПРИМЕРЫ Данные булевы функции записать в виде многочлена Жегалкина 1) х /\ (x \/ y) 1 способ: (x /\ x) \/ (x /\ y) = 0 \/ (x /\ y) = x /\ y = x ∙ y 2 способ: x ∙ ((1 + x) \/ y) = x ∙ (1 + x + y + (1 + x) ∙ y) = x ∙ (1 + x + y + y + x ∙ y) = x ∙ (1 + x + x ∙ y) = x + x + x ∙ y = x ∙ y
№ слайда 8
ПРИМЕРЫ Данные булевы функции записать в виде многочлена Жегалкина 2) х → y Ответ: 1 + x + xy 3) х ↔ y Ответ: 1 + x + y 4) х ↓ y Ответ: 1 + x + у + xy 5) х | у Ответ: 1 + xy
№ слайда 9
ПРИМЕР Данный многочлен Жегалкина представить в виде булевой функции 1 + x + z + xz + xy + xyz Ответ: z /\ (x \/ y)
№ слайда 10
ПРИМЕР Данный многочлен Жегалкина представить в виде булевой функции 1 + x + z + xz + xy + xyz (1 + z) + x (1 + z) + xy(1 + z) = (1 + z) (1 + x + xy) = z /\ (1 + x(1 + y)) = z /\ (1 + x /\ y) = z /\ x /\ y = z /\ (x \/ y)
Бесплатно
| Автор | |
|---|---|
| Дата добавления | 21.12.2018 |
| Раздел | Высшая математика |
| Подраздел | Презентация |
| Просмотров | 2712 |
| Номер материала | 5999 |