
Презентация "Числовые последовательности"

Краткое описание документа:
Презентация «Числовые последовательности» представляет учебный материал, обеспечивающий наглядность объяснения учителя на уроке по данной теме. С помощью презентации учитель более эффективно может решить задачи обучения. Презентация демонстрирует теоретический материал по теме «Числовые последовательности», формирует понятие о числовых последовательностях, их видах, связанных с ними формулах.


Представление учебного материала в форме презентации имеет множество преимуществ, которые дают возможность улучшить запоминание материала учениками, углубить понимание определений и понятий. Используемые в презентации анимационные эффекты помогают удерживать внимание учеников на изучаемом предмете. Также анимация улучшает подачу информации, структурирует ее, способствует лучшему пониманию. Запоминание определений и понятий улучшает их выделение при помощи цвета и других приемов.


Презентация начинается с определения числовой последовательности. Она определяется как функция вида y=f(x), xϵN, иначе называемая функцией натурального аргумента. На экране отображаются варианты обозначения последовательности y=f(n) или y1, y2,…, yn, или (yn).
На втором слайде представлены варианты, каким способом задается числовая последовательность. В качестве примера словесного способа задания дается последовательность 2, 3, 5,…, 29,… Также описываются варианты аналитического способа задания последовательности. В качестве примеров продемонстрированы yn=n3. Отмечается, что сама последовательность при этом являет собой последовательность чисел 1, 8, 27, 64, …, n3, … Аналитическое представление последовательности позволяет найти любой член последовательности. К примеру, для n=9 у9=93=729. Также при известном члене последовательности можно определить его порядковый номер – для yn=1331 можно определить, что n3=1331, то есть его номер n=11. Представлен еще один пример аналитического задания последовательности yn=С. Очевидно, в данной последовательности все ее члены равны С.


Ученикам уже известны примеры числовых последовательностей, которые были изучены ранее – арифметическая и геометрические прогрессии. Для задания таких последовательностей применялся рекуррентный способ задания. Напоминается, что арифметическая прогрессия задается соотношением а1=а, аn+1=an+d, в которых aи d – некоторые числа, а d – разность прогрессии. Также напоминается рекуррентное задание геометрической прогрессии, в которой b1=b, bn+1=bnq, где bи q – некоторые числа, не равные нулю, а q – знаменатель прогрессии.
На слайде 4 дается определение последовательности, что ограничена сверху. Для такой последовательности характерно, что все члены последовательности не превышают определенного числа.


Следующий слайд дает общее представление о последовательности, ограниченной сверху через выполнение неравенства yn<=M, где число М, ограничивающее последовательность иначе называется верхней границей последовательности. Определение выделено цветом для запоминания понятия. Дается пример последовательности, что ограничена сверху - -1, -8, -27, -64, …, -n3, … Отмечается, что верхней границей данной последовательности является число М=-1, а также больше него.

Аналогично верхней границе, рассматривается понятие нижней границы. Перед введением понятия рассматривается, что означает, когда последовательность ограничена снизу. Согласно определению, данному на слайде 7, последовательность будет ограниченной снизу, если значения членов не меньше определенного числа. Далее дается общее определение последовательности, что ограничена снизу, как последовательности, для которой существует число, значение которого всегда меньше или равно значений членов последовательности. Иначе это число называется нижней границей последовательности. Определение выделено цветом и рекомендовано к запоминанию. На слайде 9 приводится пример последовательности, ограниченной снизу. Отмечается, что последовательность 0,1,2,…, (n-1), …является ограниченной снизу, и эта граница равна 0 или меньшее число.


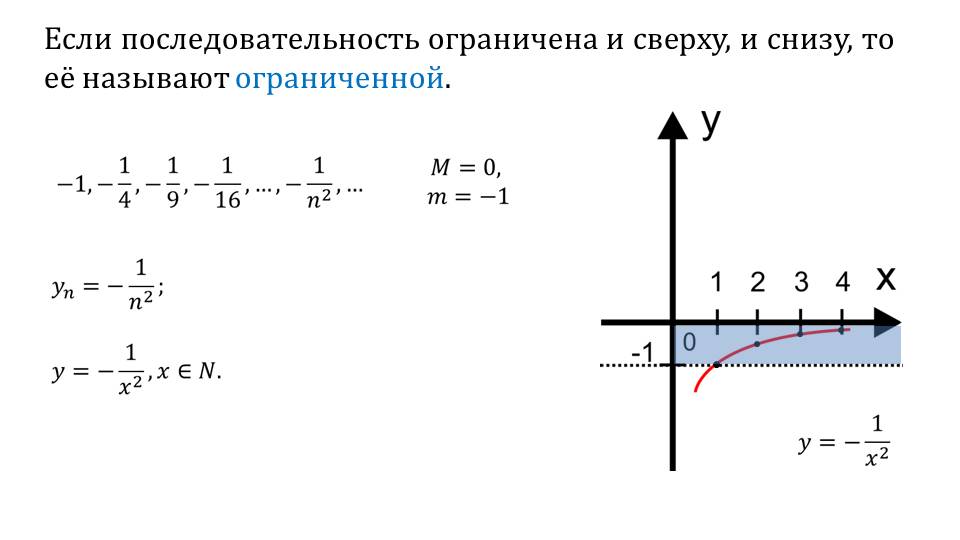
Слайд 10 демонстрирует определение ограниченной последовательности как числовой последовательности, ограниченной и сверху, и снизу. Примером служит последовательность -1, -1/4, -1/9, -1/16,…, -1/n2,… При этом верхней границей последовательности является М=0, а нижней m=-1. Общий член последовательности выражается формулой yn=-1/n2. Последовательность задается аналитическим способом yn=-1/х2, где хϵN. На рисунке строится график такой функции, демонстрирующий множество точек, удовлетворяющих условию и представляющих собой числовую последовательность.
Далее раскрывается геометрический смысл понятия ограниченности последовательности. Отмечается, что ограниченность означает, что все числа последовательности лежат на определенном отрезке числовой оси. На рисунке приводится пример последовательности, описанной в предыдущем слайде. На числовой оси выделен отрезок, содержащий значения членов последовательности.


На слайде 12 дано определение возрастающей последовательности. Отмечается, что последовательность будет возрастающей при выполнении условия у1<y2<y3<…<yn<yn+1<… Пример возрастающей последовательности 1, 3, 5,…, 2n-1,… Очевидно, каждый следующий член последовательности больше предыдущего, то есть 1<3<5<…<2n-1<2(n+1)<…
Определение убывающей последовательности описано на слайде 14. Отмечается, что условием для определения такой прогрессии является у1>y2>y3>…>yn>yn+1>… В качестве примера подобной последовательности приводится 1, 1/3, 1/5, …, 1/(2n-1), … очевидно, что для нее выполняется условие 1>1/3>1/5>…>1/(2n-1)>1/2(n+1)-1>… На слайде 15 также отмечается, что убывающие и возрастающие последовательности составляют ряд монотонных последовательностей.
На последнем слайде приводятся примеры последовательностей, тип которых нужно определить. Так, последовательность -1,2,-3,4,…,(-1)nn, … не возрастает и не убывает, то есть не является монотонной. Последовательность yn=3n монотонно возрастает. При этом отмечено, что последовательности вида yn=аn возрастают при а>1. В третьем примере отмечается, что последовательность yn=(1/5)n убывающая. В общем случае последовательность yn=аn убывающая для любого 0<а<1.


Презентация «Числовые последовательности» может использоваться в ходе проведения традиционного урока алгебры для повышения его эффективности. Также данный материал поможет обеспечить наглядность объяснения в ходе дистанционного обучения.
| Автор | |
|---|---|
| Дата добавления | 27.07.2014 |
| Раздел | Алгебра |
| Подраздел | Презентация |
| Просмотров | 4098 |
| Номер материала | 814 |