
Презентация "Длина дуги числовой окружности"

Краткое описание документа:
В современном образовательном процессе большую роль играют интерактивные методы обучения. Они включают в себя использование различных современных методов и технологий при процессе образования. К материалам, которые относятся к интерактивному обучению относят презентации, видео- аудиоуроки и т.д.

С помощью данной презентации можно подробной ознакомиться с нахождением длины дуги числовой окружности.
Одной из важных тем при изучении числовой окружности является длина дуги. В данной презентации будет рассмотрено нахождение длины дуги числовой окружности и продемонстрированы интересные развивающие задачи.
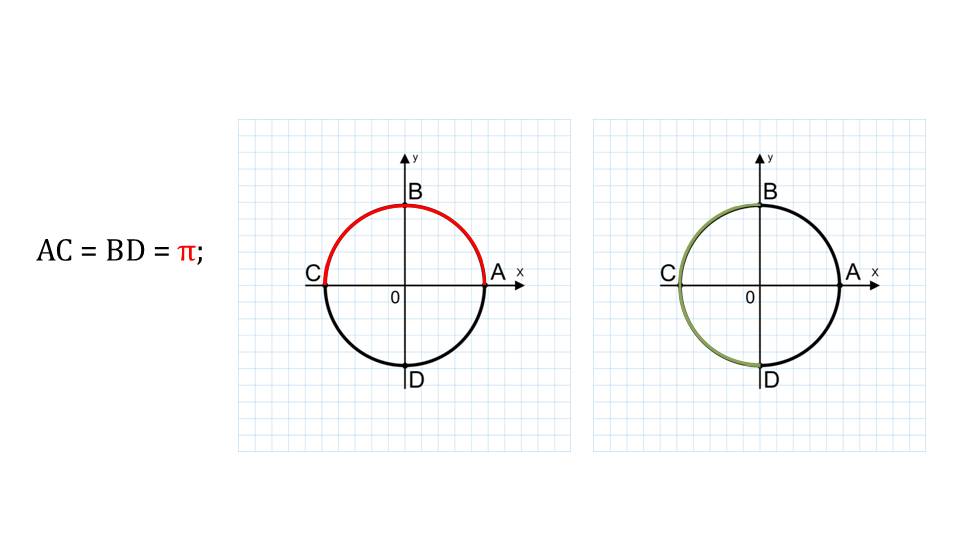
Для начала напоминается обозначение длины окружности, формула нахождения длины произвольной окружности, обозначение радиуса числовой окружности, которой равняется единице и длин единичной окружности. Последнее, как уже известно, является постоянной величиной, равной 6,28. Это можно очень просто доказать, подставив в формулу значение радиуса.
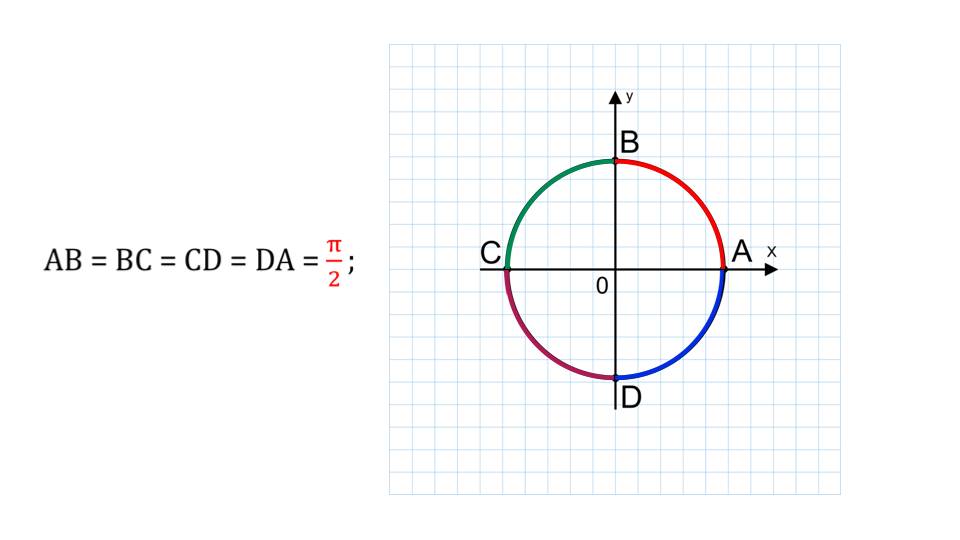

Единичная окружность иметь под одной дуге на каждую полуплоскость. Половины длины окружности создает угол, равный Пи. Таким образом, дуга окружности на одной полуплоскости будет равняться Пи, деленная на два.
На следующих слайдах рассматриваются примеры. Для того чтобы их решить, нужно иметь хорошие геометрические знания. Решения приведены подробным образом. Можно изучить и без помощи учителя. В каждой задаче приведены графики с обозначениями.
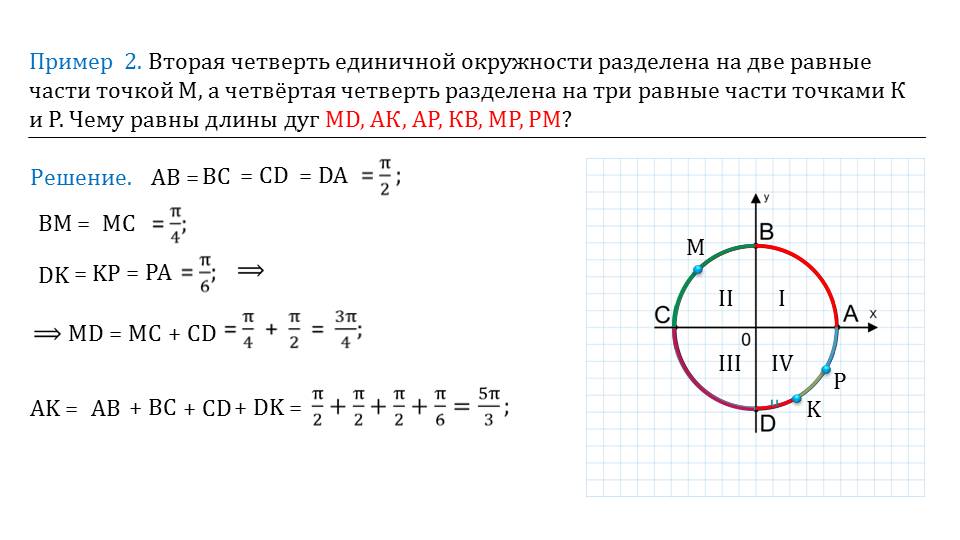

Данная презентация составлена очень грамотно и имеет четкую структуру. Она является понятной и полезной для каждого десятиклассника, которому необходимо изучить данную тему в курсе алгебры. С помощью нее можно подготовиться к следующему уроку или к контрольной работе.
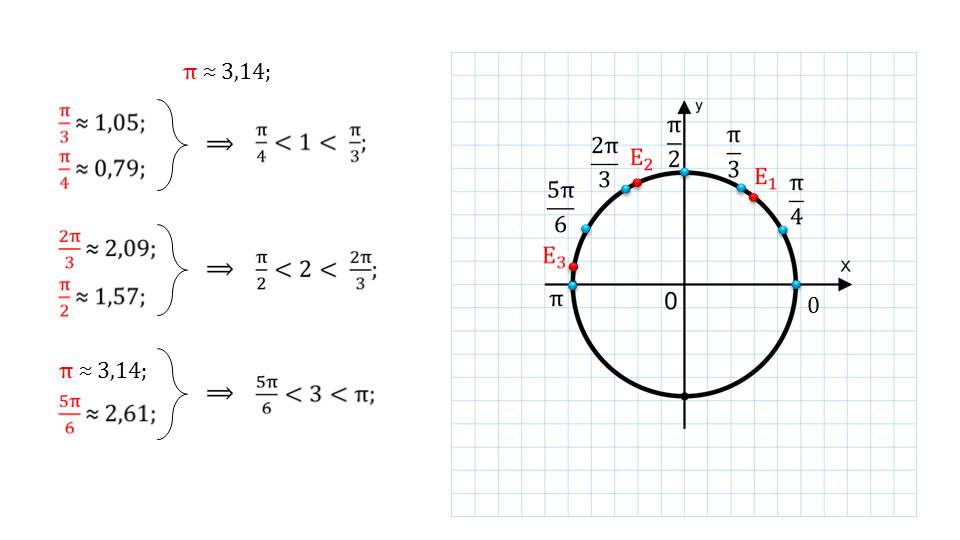
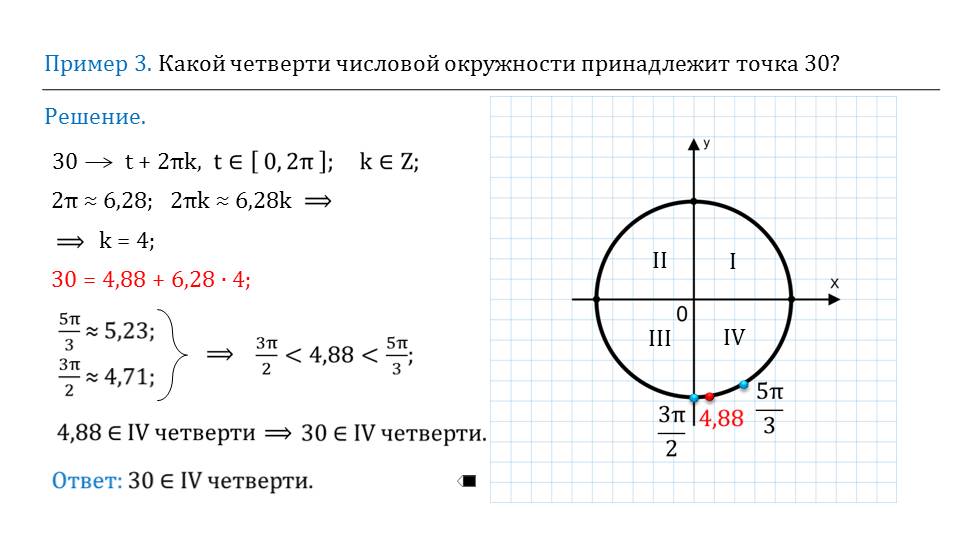
Как видим, презентация достаточно большая и информативная. Необходимо уделить время и проявить усидчивость, чтобы понять и запомнить каждый момент как следует хорошо. Примеры на практике закрепят изученную информацию.
| Автор | |
|---|---|
| Дата добавления | 27.07.2014 |
| Раздел | Алгебра |
| Подраздел | Презентация |
| Просмотров | 3259 |
| Номер материала | 784 |