
Презентация "Движения. Осевая симметрия"

Краткое описание документа:
Презентация «Движения. Осевая симметрия» представляет наглядный материал для объяснения на школьном уроке математики основных положений данной темы. В данной презентации осевая симметрия рассматривается как еще один вид движения. В ходе презентации ученикам напоминается изученное понятие центральной симметрии, дается определение осевой симметрии, доказывается положение о том, что осевая симметрия является движением, а также описывается решение двух задач, в которых необходимо оперировать понятием осевой симметрии.
Осевая симметрия является движением, поэтому ее представление на классной доске вызывает сложности. Более четкие понятные построения можно сделать с помощью электронных средств. Благодаря этому построения хорошо видны с любой парты в классе. На рисунках есть возможность выделить цветом детали построения, акцентировать внимание на особенностях операции. С той же целью используются анимационные эффекты. С помощью инструментов презентации учителю легче достичь целей обучения, поэтому презентация применяется для повышения эффективности урока.
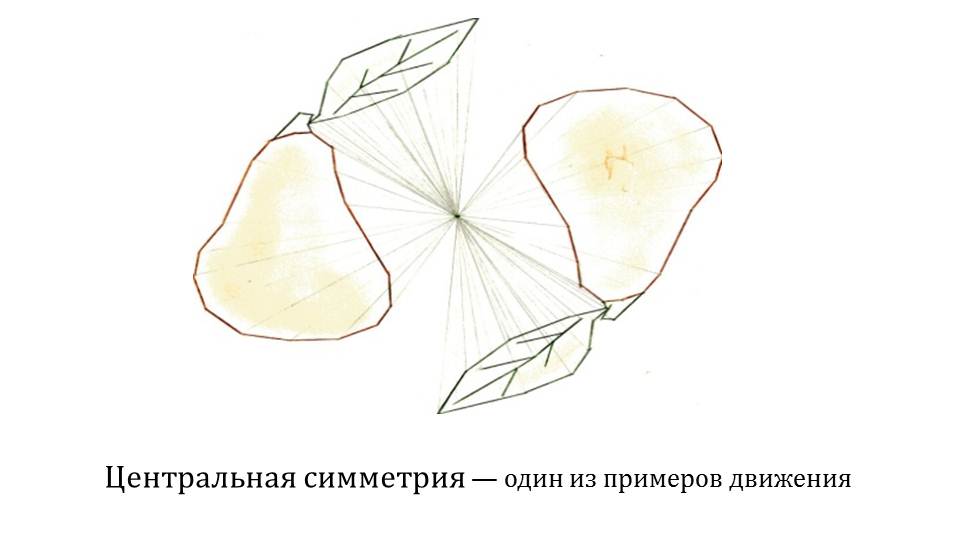
Демонстрация начинается с напоминания ученикам об изученном виде движения – центральной симметрии. Примером применения операция служит симметричное отображение нарисованной груши. На плоскости отмечается точка, относительно которой каждая точка изображения переходит в симметричную. Отображенное изображение, таким образом, перевернуто. При этом все расстояния между точками объекта сохраняются при центральной симметрии.
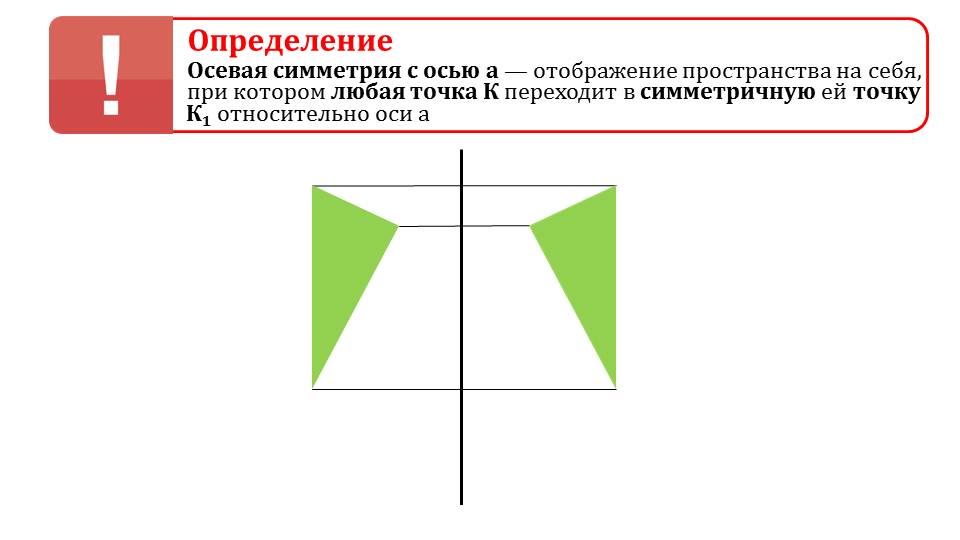
На втором слайде вводится понятие осевой симметрии. На рисунке изображен треугольник, каждая его вершина переходит в симметричную вершину треугольника относительно некоторой оси. В рамке выделено определение осевой симметрии. Отмечается, что при нем каждая точка объекта переходит в симметричную.
Далее в прямоугольной координатной системе рассматривается осевая симметрия, свойства координат объекта, отображенного с помощью осевой симметрии, в также доказывается, что при данном отображении сохраняются расстояния, что есть признаком движения. Справа на слайде изображается прямоугольная система координат Оxyz. За ось симметрии принимается ось Оz. В пространстве отмечена точка М{x;y;z}, при соответствующем отображении переходящая в М1{x1;y1;z1}. На рисунке видно, что при осевой симметрии точка сохраняет свою аппликату.
Отмечается, что среднее арифметическое абсцисс и ординат данного отображения при осевой симметрии равно нулю, то есть (x+ x1)/2=0; (y+ y1)/2=0. Иначе это свидетельствует, что x=-x1; y=-y1; z=z1. Правило сохраняется и в случае, если точка М отмечена на самой оси Оz.
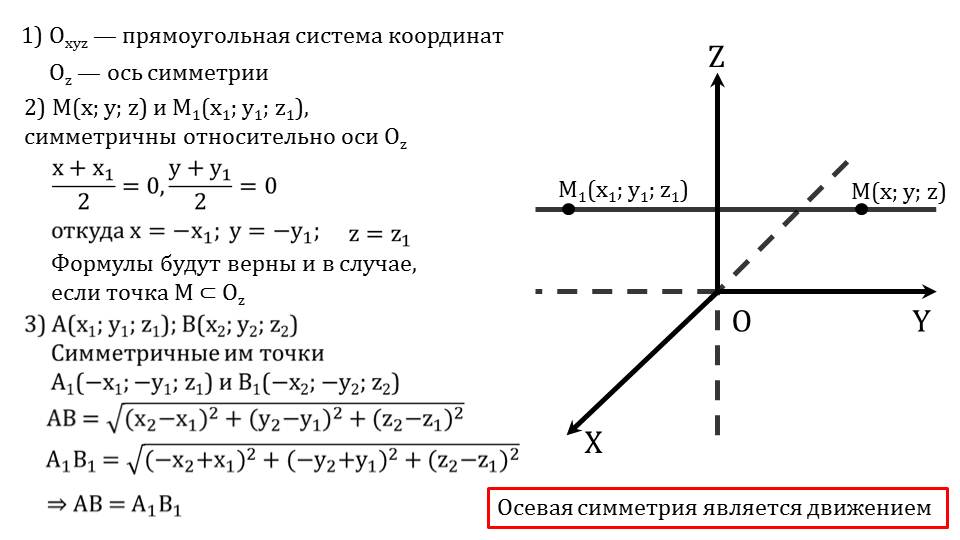
Для рассмотрения, сохраняются ли расстояния между точками при осевой симметрии, описывается операция на точками А{x1;y1;z1} и В{x2;y2;z2}. Отображаясь относительно оси Оz, описываемые точки переходят в А1{-x1;-y1;z1} и В1{-x2;-y2;z2}. Чтобы определить расстояние между точками, воспользуемся формулой, в которой расстояние вычисляется по координатам. Отмечается, что АВ=√(x2-x1)2 +(y2-y1)2+(z2-z1)2), а для отображенных точек А1В1=√(-x2+x1)2 +(-y2+y1)2+(z2-z1)2). Учитывая свойства возведения в квадрат, можно отметить, что АВ=А1В1. Это говорит о том, что расстояния сохраняются между точками – главный признак движения. Значит, осевая симметрия есть движение.
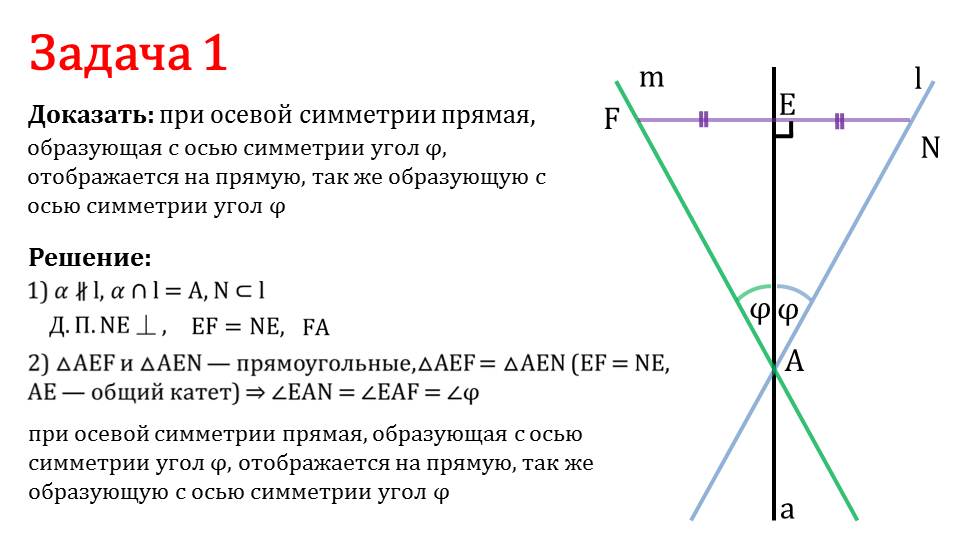
На слайде 5 рассматривается решение задачи 1. В ней необходимо доказать утверждение, что прямая, проходящая под углом φ к оси симметрии, образует с ней такой же угол φ. К задаче дается изображение, на котором начерчена ось симметрии, а также прямая m, образующая с осью симметрии угол φ, и относительно оси ее отображение – прямая l. Доказательство утверждения начинается с построения дополнительных точек. Отмечается, что прямая m пересекает ось симметрии в А. Если отметить на этой прямой точку F≠A и опустить от нее перпендикуляр на ось симметрии, получим пересечение перпендикуляра с осью симметрии в точке Е. При осевой симметрии отрезок FE переходит в отрезок NE. В результате такого построения получили прямоугольные треугольники ΔAEF и ΔAEN. Эти треугольник равны, так как АЕ является у них общим катетом, а FE = NE равны по построению. Соответственно, угол ∠EAN=∠EAF. Из этого следует, что отображенная прямая также образует с осью симметрии угол φ. Задача решена.
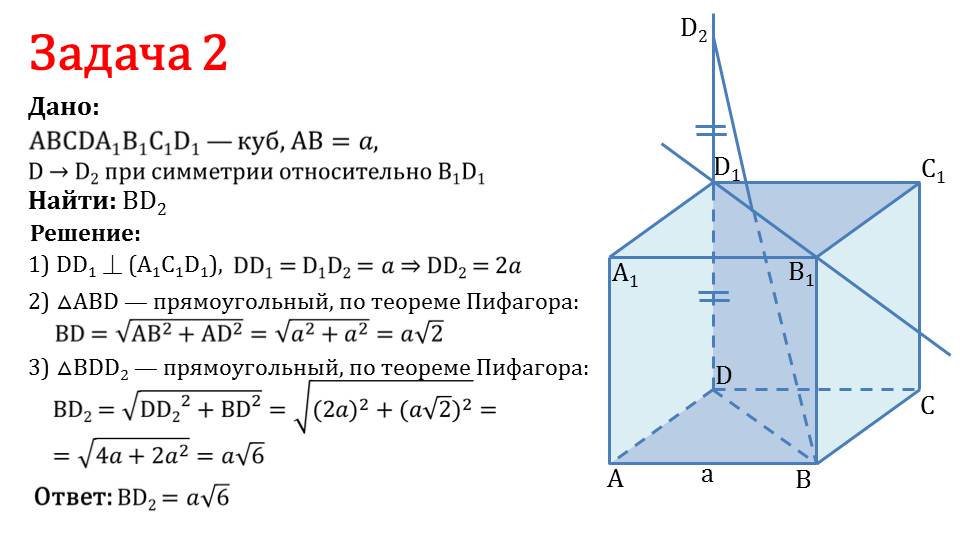
На последнем слайде рассматривается решение задачи 2, в которой необходимо дан куб ABCDA1B1C1D1 со стороной а. Известно, что после симметрии относительно оси, содержащей ребро B1D1, точка D переходит в D1. В задаче требуется найти BD2. К задаче делается построение. На рисунке изображен куб, по которому видно, что осью симметрии является диагональ грани куба B1D1. Отрезок, образующийся при движении точки D, перпендикулярен плоскости грани, которой принадлежит ось симметрии. Так как при движении сохраняются расстояния между точками, то DD1= D1D2=а, то есть расстояние DD2=2а. Из прямоугольного треугольника ΔABD по теореме Пифагора следует, что BD=√(AB2+AD2)=а√2. Из прямоугольного треугольника ΔВDD2 следует по теореме Пифагора BD2=√( DD22+ВD2)=а√6. Задача решена.
Презентация «Движения. Осевая симметрия» используется для повышения эффективности школьного урока математики. Также этот метод наглядности поможет учителю, осуществляющему дистанционное обучение. Материал может быть предложен для самостоятельного рассмотрения учениками, которые недостаточно хорошо усвоили тему урока.
| Автор | |
|---|---|
| Дата добавления | 07.11.2014 |
| Раздел | Геометрия |
| Подраздел | Презентация |
| Просмотров | 6033 |
| Номер материала | 964 |