
Презентация "Формулы приведения"

Краткое описание документа:
Данная презентация является отличным учебным материалом, который посвящен теме «Формулы приведения». Это одна из важных тем из области изучения тригонометрии, которая долгое время будет изучаться в 10 классе.


В процессе будут решаться множество алгебраических и геометрических задач, с использованием терминов тригонометрии.
Первый слайд презентации говорит о значении формул приведения в тригонометрии. Функции определенного вида может быть упрощена с помощью данных правил, которым посвящен данный учебный материал.


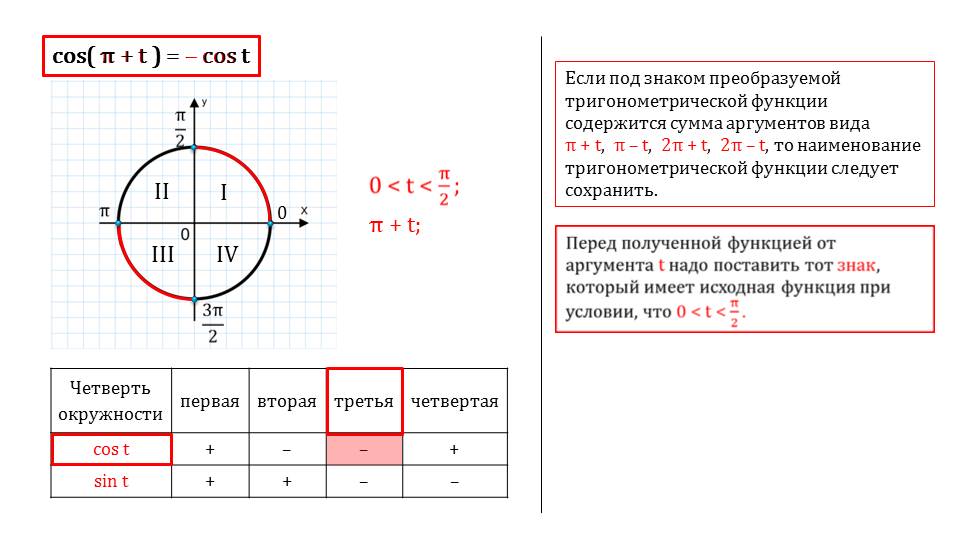
При определенных знаках функции, которая подвергнется преобразованиям, наименование тригонометрической функции сохраняется. В других случаях – синусы меняются на косинусы, тангенсы на котангенсы, и, соответственно, наоборот.
На следующем слайде говорится о том, каким образом необходимо поставить правильно знак. Эти правила необходимо запомнить.

Все эти формулы приведения можно записать через градусную меру. Как это делается, показывается на последующем слайде.
Все эти теоретически просмотренные правили приведения тригонометрических функций подробно демонстрируются в наглядной форме далее.
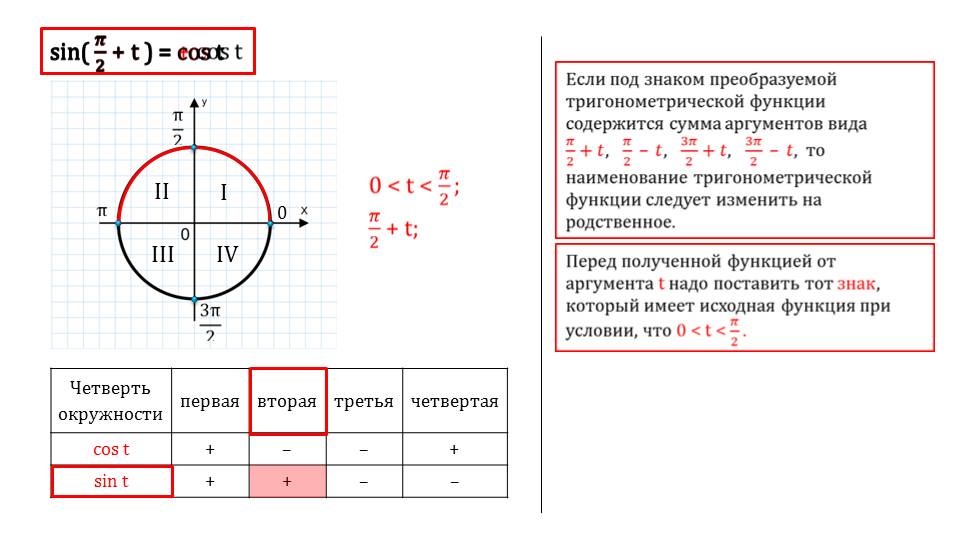
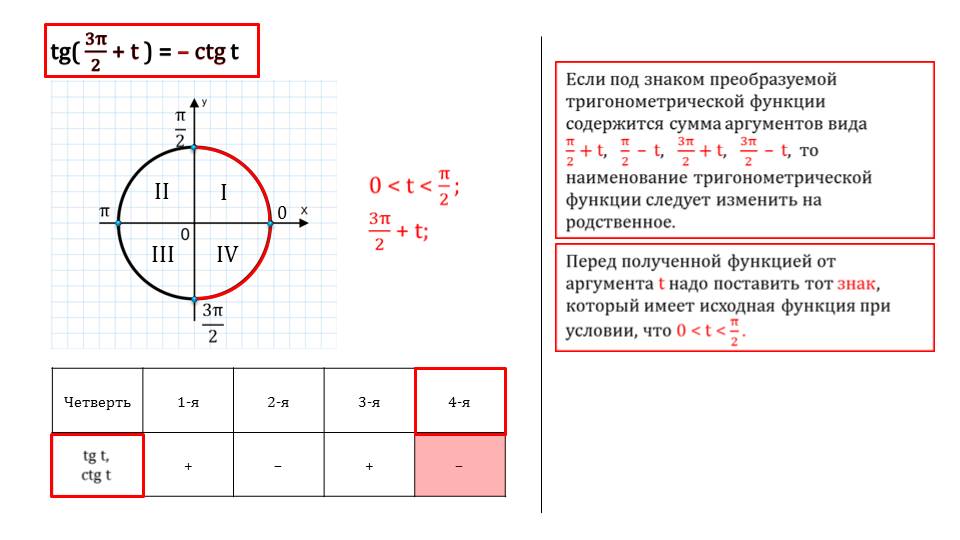
Приведена числовая единичная окружность со всеми необходимыми обозначениями, также видны периоды, обозначены рассматриваемые дуги, приведена таблица, на которой с помощью анимационных эффектов демонстрируется все шаг за шагом.
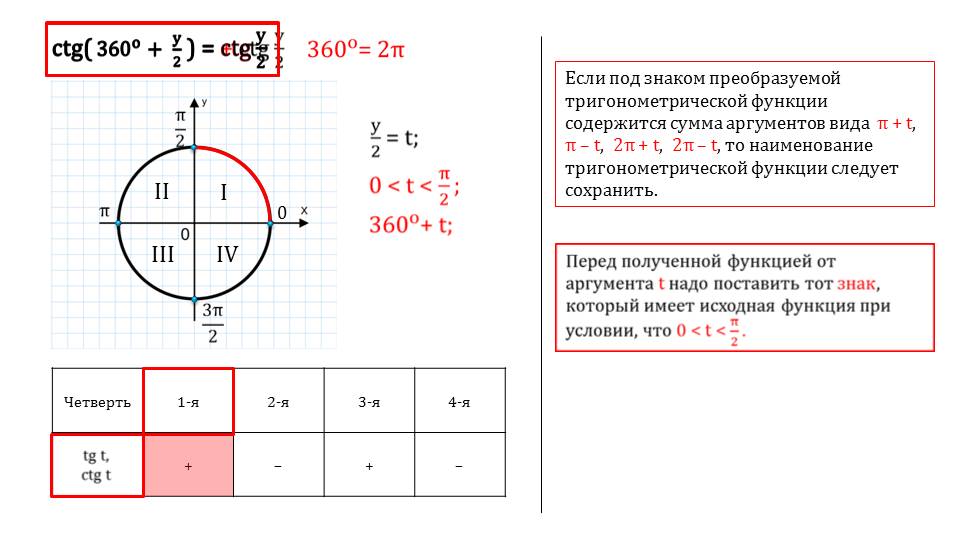

Подобных слайдов – 4. Все они разъясняются формулы приведения. Просмотрев все эти слайды, школьнику должна стать понятной вся суть.
Далее приводится первый пример. В нем предлагается найти синус некоторого градуса, больше 180. Знак отрицательный. С помощью использования формулы приведения решается данный пример намного проще. Также все наглядно демонстрируется на таблице.


Следующий слайд содержит в себе задание, в котором требуется доказать некоторое тождество. Для его доказательства используется еще одна формула приведения.
Последующие примеры являются аналогичными. Справой стороны всех утверждений стоит единица, что подсказывает школьникам, к какой формуле в результате они должны прийти.


Презентация поможет подготовиться к самостоятельным работам, в которых содержатся тригонометрические выражения, для решения, доказательства или упрощения которых необходимо понимать основные формулы, принципы и методы.
| Автор | |
|---|---|
| Дата добавления | 27.07.2014 |
| Раздел | Алгебра |
| Подраздел | Презентация |
| Просмотров | 5611 |
| Номер материала | 792 |