
Презентация «Функция y=ax^2, ее график и свойства»

Краткое описание документа:
Презентация «Функция y=ax2, ее график и свойства» является наглядным пособием, которое создано для сопровождения объяснения учителя по данной теме. В данной презентации подробно рассматривается квадратичная функция, ее свойства, особенности построения графика, практическое приложение используемых методов решения задач в физике.


Предоставляя высокую степень наглядности, данный материал поможет учителю повысить эффективность обучения, даст возможность более рационально распределить время на уроке. При помощи анимационных эффектов, выделения понятий и важных моментов цветом, внимание учеников акцентируется на изучаемом предмете, достигается лучшее запоминание определений и хода рассуждения при решении задач.


Презентация начинается с ознакомления с названием презентации и понятием квадратичной функции. Подчеркивается важность данной темы. Ученикам предлагается запомнить определение квадратичной функции как функциональной зависимости вида y=ax2+bx+c, в которой является независимой переменной, а – числа, при этом a≠0. Отдельно на слайде 4 отмечается для запоминания, что областью определения данной функции является вся ось действительных значений. Условно данное утверждения обозначается D(x)=R.


Примером квадратичной функции является важное ее приложение в физике – формула зависимости пути при равноускоренном движении от времени. Параллельно на уроках физики ученики изучают формулы различных видов движения, поэтому умение решать подобные задачи им будет необходимо. На слайде 5 ученикам напоминается, что при движении тела с ускорением и на начало отсчета времени известен пройденный путь и скорость движения , то функциональная зависимость, представляющая такое движение, будет выражаться формулой S=(at2)/2+v0 t+S0. Ниже приводится пример превращения данной формулы в заданную квадратичную функцию, если значения ускорения =8, начальной скорости =3 и начального пути =18. В этом случае функция приобретет вид S=4t2+3t+18.
На слайде 6 рассматривается вид квадратичной функции y=ax2, в котором она представляется при. Если же =1, то квадратичная функция имеет вид y=x2. Отмечается, что графиком данной функции будет парабола.
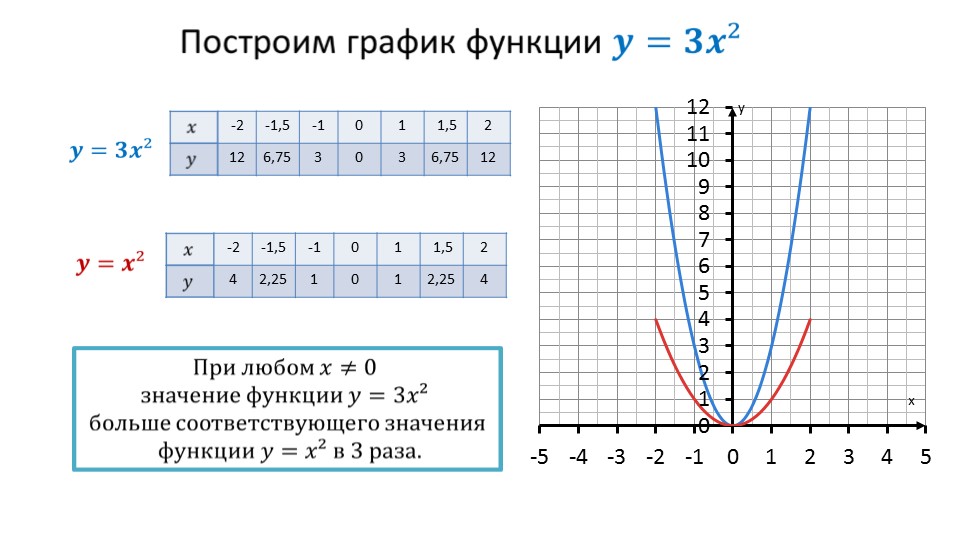
Следующая часть презентации посвящена построению графика квадратичной функции. Предлагается рассмотреть построение графика функции y=3x2. Сначала в таблице отмечается соответствие значений функции значениям аргумента. Отмечается, что отличие построенного графика функции y=3x2 от графика функции y=x2 в том, что каждое значение ее будет больше соответствующего в три раза. В табличном представлении эта разница хорошо отслеживается. Рядом в графическом представлении также хорошо заметна разница в сужении параболы.


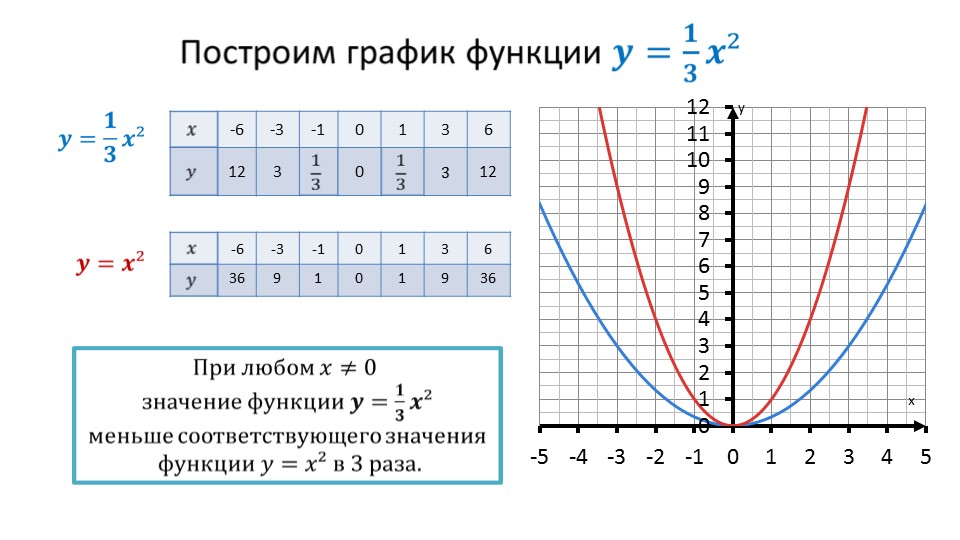
На следующем слайде рассматривается построение графика квадратичной функции y=1/3 x2. Для построения графика необходимо в таблице указать значения функции в ряде ее точек. Отмечается, что каждое значение функции y=1/3 x2 меньше соответствующего значения функции y=x2 в 3 раза. Данная разница, кроме таблицы, хорошо видна и на графике. Ее парабола более расширена относительно оси ординат, чем парабола функции y=x2.
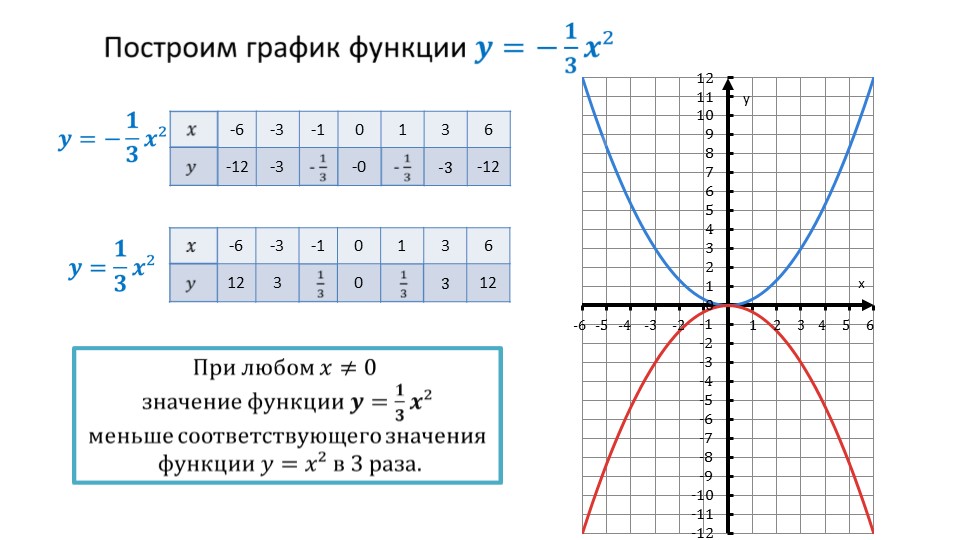
Примеры помогают усвоить общее правило, согласно которому можно затем более просто и быстро производить построение соответствующих графиков. На слайде 9 выделено отдельно правило, что график квадратичной функции y=ax2 можно построить в зависимости от значения коэффициента растяжением или сужением графика. Если a>1, то график растягивается от оси х в раз. Если же 0<a<1, то к оси x график сжимается в 1/a раза. В следующей части презентации рассматривается поведение квадратичной функции y=ax2 в случае, когда коэффициент отрицательный. Предлагается построить график функции y=-1/3 x2. В табличном представлении функции обращается внимание, что значение функции y=1/3 x2 меньше соответствующих значении функции y=x2 в 3 раза. Видно, что сформированные значения функции y=-1/3 x2 по абсолютному значению равны со значениями соответствующих аргументов функции y=1/3 x2, однако с противоположным знаком. На графике эта разница отражается в отражении графика функции относительно оси абсцисс вниз.
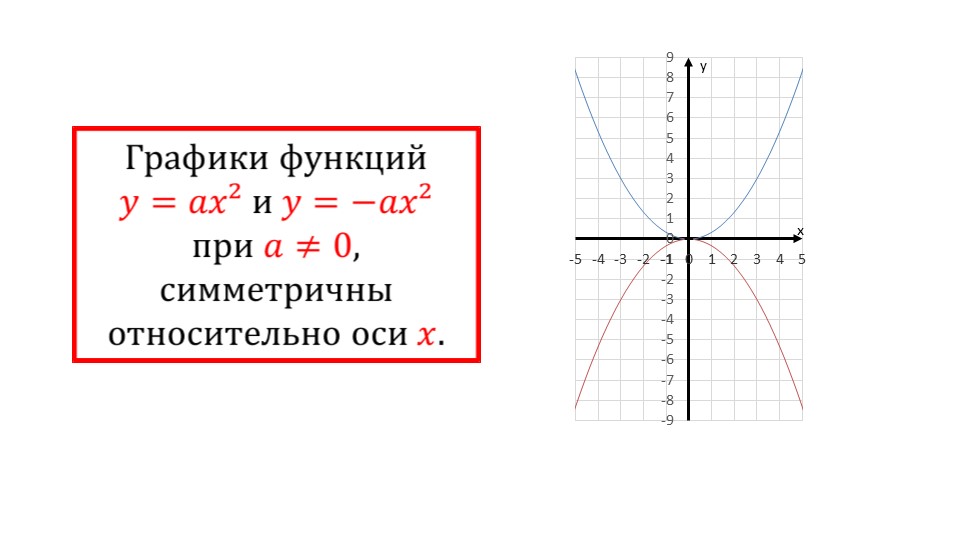
Вывод о симметричности графиков функций y=ax2 и y=-ax2 (при ≠0) относительно оси абсцисс отдельно выделен на слайде 12 для запоминания и наглядно отображен на соответствующем графике. Далее понятие о графике квадратичной функции y=x2 распространяется на более общий случай функции y=ax2, утверждая, что такой график также будет называться параболой.


На слайде 14 рассматриваются свойства квадратичной функции y=ax2 при положительном . Отмечается, что ее график проходит через начало координат, а все точки, кроме , лежат в верхней полуплоскости. Отмечена симметричность графика относительно оси ординат, уточняя, что противоположным значениям аргумента соответствуют одинаковые значения функции. Указано, что промежуток убывания данной функции (-∞;0], а возрастание функции выполняется на промежутке. Значения данной функции охватывают всю положительную часть действительной оси, нулю она равна в точке , а наибольшего значения не имеет.
На слайде 15 описываются свойства функции y=ax2, если отрицательный. Отмечается, что ее график также проходит через начало координат, но все его точки, кроме, лежат в нижней полуплоскости. Отмечена симметричность графика относительно оси, и противоположным значениям аргумента соответствуют равные значения функции. Возрастает функция на промежутке, убывает на. Значения данной функции лежат в промежутке, нулю она равна в точке, а наименьшего значения не имеет.


Обобщая рассмотренные характеристики, на слайде 16 выводится, что ветви параболы направлены вниз при, а вверх – при. Парабола симметрична относительно оси , а вершина параболы располагается в точке ее пересечения с осью. У параболы y=ax2 вершина – начало координат.
Также важный вывод о преобразованиях параболы отображается на слайде 17. На нем представлены варианты преобразований графика квадратичной функции. Отмечено, что график функции y=ax2 преобразуется симметричным отображением графика относительно оси . Также возможно сжатие или растяжение графика относительно оси.
На последнем слайде делаются обобщающие выводы о преобразованиях графика функции. Представлены выводы о том, что график функции получается симметрическим преобразованием относительно оси. А график функции получается из сжатием или растяжением исходного графика от оси. При этом растяжение от оси в раз наблюдается в случае, когда. Сжатием к оси в 1/a раз график образуется в случае.


Презентация «Функция y=ax2, ее график и свойства» может быть использована учителем в качестве наглядного пособия на уроке алгебры. Также данное пособие хорошо раскрывает тему, давая углубленное понимание предмета, поэтому может быть предложена для самостоятельного изучения учениками. Также данный материал поможет учителю дать объяснение в ходе дистанционного обучения.
| Автор | |
|---|---|
| Дата добавления | 29.08.2014 |
| Раздел | Алгебра |
| Подраздел | Презентация |
| Просмотров | 9183 |
| Номер материала | 643 |