
Презентация «Корень n-степени»

Краткое описание документа:
Презентация «Корень n-степени» содержит наглядный учебный материал для урока алгебры по данной теме. В презентации описаны свойства и особенности, нахождение математического корня n-степени из некоторого числа. При помощи данного материала учитель может более рационально использовать время урока, повысить эффективность обучения.


В презентации используются анимационные эффекты, «оживляющие» объяснение, повышающие концентрацию внимания ученика. Они также помогают выделить важные детали для лучшего понимания и запоминания.
Презентация начинается с представления темы урока и определения квадратного корня. Ученики уже имеют представление о квадратном корне. На данном уроке задача учителя – расширить и углубить знания учеников о корнях, формировать навыки нахождения корней из числа. На экран выведено определение квадратного корня из как числа, квадрат которого будет равен. Аналогично понятию квадратного корня вводится понятие корня -степени, которое означает, степень данного числа равна.

На слайде 3 приведены примеры нахождения корня -степени из различных чисел. Отмечается, что значение корня 5 степени из 243 формируется из числа, возведя которое в 5 степень, получаешь 243. Также уточняется случай выделения корня четной степени из числа. Указано, что значение может принимать как положительные, так и отрицательные значения, так как при возведении в четную степень значение будет только положительным. Так, 6√64=±2, так как при возведении 2 в степень 6 получаешь число 64. Ниже дается обозначение квадратного корня 2√ и кубического корня 3√.

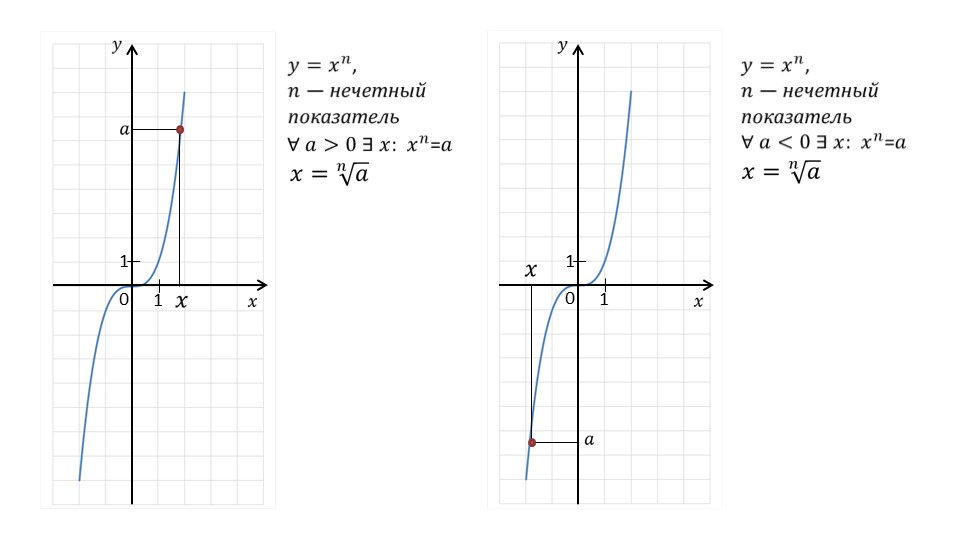
На слайде 4 отражена особенность формирования значения степенной функции с нечетным показателем степени. На графиках отмечены значения степенной функции на оси ординат. Выполняя обратную операцию к степени, значение корня формируется соответствием абсциссы точки, принадлежащей графику, ее ординате. Таким же образом формируется отрицательное значение корня нечетной -степени из отрицательного числа.
Для формирования умения описывать математическим языком операции с корнями на слайде 5 выделено письменное обозначение корня – степени n√a, его устное обозначение как корня n-степени из a. При этом a называется подкоренным выражением, а n – показателем корня.

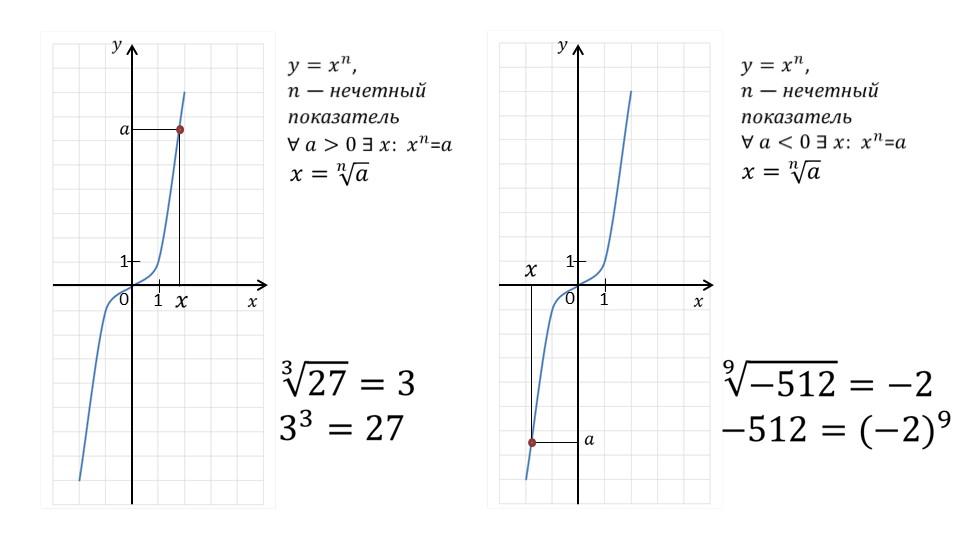
На рисунках слайда 6 поясняется механизм формирования значения и свойств корня -степени из отрицательного числа. На графике отмечено, как формируется положительное значение 3 корня 3-степени из 27 и отрицательное значение -2 корня 9-степени из -512.
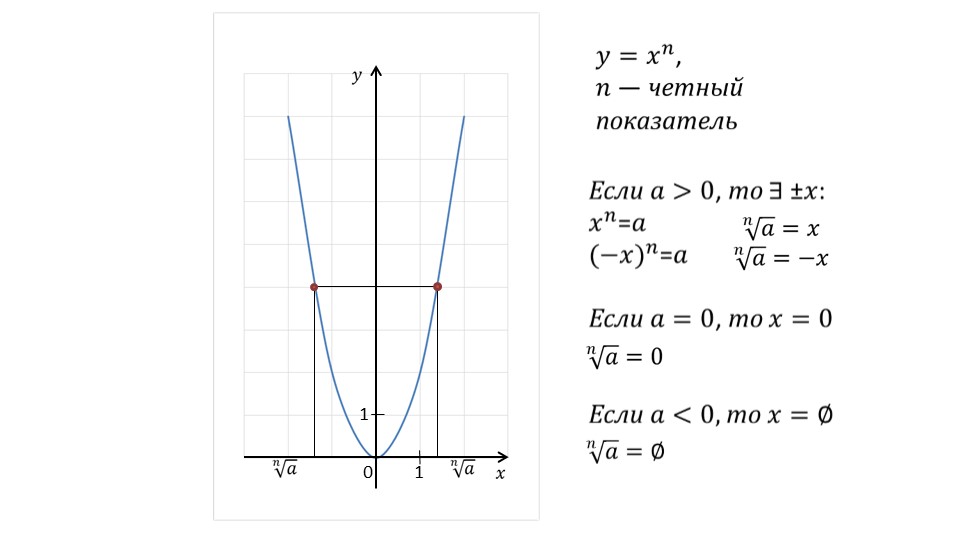
Формирование значения и свойств корня четной степени описывается на рисунке слайда 7. Изображена парабола – график функции y=xn, где – четный показатель степени. На графике описывается, как значение функции принимает положительные значения и при положительном, и при отрицательном значении. Соответственно, значение корня из положительного числа также может быть отрицательным или положительным числом. В соответствии с механизмом формирования значения корня отмечается, что n√a=0, если a=0. При этом для корней четной степени n√a=∅ при отрицательных значениях.


На слайде 8 отображаются обозначения, которые необходимо использовать при решении задач на нахождение корня четной -степени. Отмечается, что для положительных неотрицательный корень обозначается как n√a, а отрицательный корень из обозначается как - n√a. Для четного значения степени выражение n√a при отрицательных значениях не имеет смысла. Ниже приведен пример нахождения корня 4-степени из 16. Так как при возведении в 4 степень числа 2 формируется значение 16, то 4√16=2. Также отмечается, что практикуется сокращенная запись квадратного корня – показатель степени корня не пишется.


На слайде 10 отмечается правило, когда выражение n√a имеет смысл. Выделено, что n√a при нечетном значении степени корня имеет смысл для подкоренного значения любого знака, а при четных значениях степени корня подкоренное значение может быть только положительным. Учитывая данные утверждения, формулируется одно из свойств корня, которое выделено цветом для запоминания: (n√a)n=a. На слайде 11 выводы из данных утверждений обобщаются, отмечая, что выражение n√a для неотрицательного подкоренного значения имеет смысл при любых значениях степени, при этом его значение – неотрицательное число. И это число называется арифметическим корнем -степени из . Данное утверждение как важное определение выделено отдельно на слайде 12 для запоминания.


Далее свойства корня нечетной степени позволяют сделать некоторые преобразования, которые можно обозначить n√(-a)=-n√a. Отмечается, что для положительного и нечетного значения данное равенство всегда будет верно. Примером применения данного свойства служит нахождение корня 5 степени из -32. Решение выглядит так: 5√(-32)=-5√(32)=-2.
Также обращается внимание учеников на еще одну запись, принятую при записи корней, которая представляет собой степень, записанную в виде дроби. Так выражение n√a иначе может быть записано a1/n.

В последней части презентации описывается программа нахождения корня некоторой степени из положительного числа. Представлена очередность выполнения операций для нахождения значения выражения.
Презентация «Корень – n-степени» может быть использована для наглядности при объяснении темы урока в школе. Также данный материал может послужить инструментом дистанционного обучения, помочь разобраться со свойствами корня – n-степени при самостоятельном изучении темы.
| Автор | |
|---|---|
| Дата добавления | 29.08.2014 |
| Раздел | Алгебра |
| Подраздел | Презентация |
| Просмотров | 10004 |
| Номер материала | 647 |