
Презентация «Квадратный трехчлен и его корни»

Краткое описание документа:
Презентация «Квадратный трехчлен и его корни» создана для наглядного представления учебного материала по данной теме. В ходе презентации представлены основные определения, примеры квадратного трехчлена, нахождения его решений, а также приложение изученного материала для решения практических задач.


Форма презентации дает возможность более наглядно представить материал, чем при обычном объяснении учителя на уроке. Четкое изображение, анимационные эффекты, наглядное выделение важных понятий повышает эффективность обучения, способствует лучшему усвоению материала.
Презентация начинается с представления названия урока. Понятие квадратного вытекает из понятия многочлена с одной переменной. Ученикам напоминается, что такое многочлен с одной переменной – примеры таких многочленов даны на экране. Затем подается определение корня многочлена как значения переменной, при котором данный многочлен обращается в нуль. Определение представлено на экране, понятие корня выделено цветом для лучшего запоминания.


На следующем слайде представлено решение задачи нахождения корней многочлена. Предлагается найти корни многочлена x3-4x=0. Для нахождения корней данного многочлена, он представляется в виде произведения. После вынесения общего множителя х за скобки и разложения на множители разности квадратов получаем выражение вида x(x-2)(x+2)=0. Очевидно, что данный многочлен обращается в нуль при следующих значениях х: x1=0, x2=2, x3=-2. Это и есть решение данной задачи.


Далее производится переход от понятия многочлена к понятию квадратного трехчлена, отмечая, что многочлен второй степени, содержащий только одну переменную, и называется квадратным трехчленом. Определение квадратного трехчлена выделено на экране. Более точное определение представляет квадратный трехчлен в виде: ax2+bx+c, где a, b, c– числовые коэффициенты, при этом а≠0. Более подробно описываются данные трехчлены на примерах. На экране отображаются квадратные трехчлены 2x2-x-5 и x2+7x-8. Отмечается, что числовые коэффициенты в первом трехчлене – a=2, b=-1, c=-5, а во втором трехчлене – a=1, b=7, c=-8.


Далее рассматриваются частные случаи, когда общий вид квадратного трехчлена несколько видоизменяется, так как его коэффициенты b или c, или оба одновременно – равны нулю. Пример такого трехчлена приведен на слайде 9: это многочлен 5x2-2x, в котором a=5, b=-2, c=0.
Нахождение корней квадратного трехчлена производится аналогично приведенным ранее примерам нахождения корней многочлена. Для поиска корней трехчлена необходимо найти корни равенства ax2+bx+c=0. На слайде 11 приводится пример нахождения корней квадратного трехчлена x2-3x-4. Для этого решается квадратное уравнение x2-3x-4=0. После расчета дискриминанта уравнения D=25, находим его корни – х1=4, х2=-1. На следующем слайде 12 описывается условие наличия и количества действительных корней данного квадратного трехчлена в зависимости от значения его дискриминанта. Отмечается, что существует два корня х1 и х2, если значение дискриминанта будет положительным. В случае дискриминанта, равного нулю, у многочлена – один корень x1. Если же при вычислении получен отрицательный дискриминант, во множестве действительных чисел нет корней.
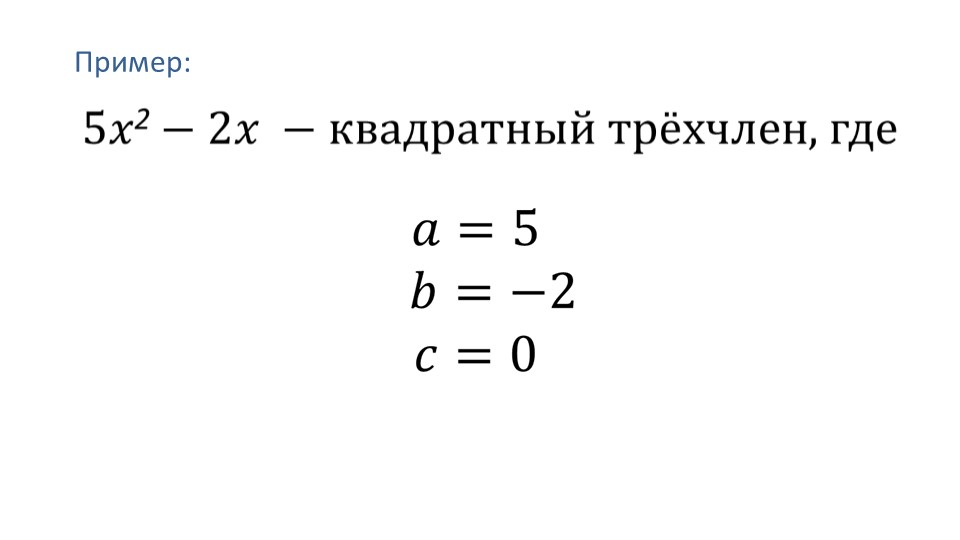

На следующем слайде утверждается, что из любого квадратного трехчлена можно выделить квадрат двучлена для представления выражения в виде ax2+bx+c=a(x-m)2+n, где mи n – числа. Данный прием поможет затем при решении множества математических и практических задач. На слайде 14 предлагается решить такое задание. Демонстрируется, каким образом можно представить квадратный трехчлен в виде квадрата двучлена и некоторого числа. Для этого в квадратном трехчлене 2x2-4x+6 выводится общий множитель 2, после чего числовой коэффициент с рабивается на слагаемые таким образом, чтобы одно из слагаемых представило необходимый числовой коэффициент для представления выражения в виде квадрата двучлена. Итоговое выражение имеет вид 2(х-1)2+4.


Последний слайд демонстрирует практическое приложение умений по нахождению корней квадратного трехчлена. Для этого предлагается доказать утверждение о том, что наибольшую площадь среди всех прямоугольников с заданным периметром 20 см имеет квадрат. Для решения данной задачи площадь прямоугольника представляется в виде произведения стороны х и стороны 10-х. После перемножения данных сторон после раскрытия скобок в итоге получается квадратный трехчлен –х2+10х. Выделив из данного трехчлена квадрат двучлена, получаем выражение –(х-5)2+25. Из данного выражения видно, что так как перед двучленом стоит знак минус, то первое слагаемое выражения может принимать только отрицательные значения и нуль. Соответственно, при х=5, когда данное слагаемое равняется нулю, общее значение выражения будет наибольшим.


После подстановки значения одной из сторон х=5, получаем, что вторая сторона при этом 10-х=10-5=5 см. То есть она также равна нулю. Утверждение доказано – прямоугольником с наибольшей площадью периметром 20 см будет квадрат со стороной 5 см.

Презентация «Квадратный трехчлен и его корни» может помочь учителю в объяснении нового материала по данной теме. Подробное понятное объяснение также может стать основой для урока при дистанционном обучении. Для более глубокого понимания материала данное пособие может быть рекомендовано ученикам при самостоятельном изучении.
| Автор | |
|---|---|
| Дата добавления | 29.08.2014 |
| Раздел | Алгебра |
| Подраздел | Презентация |
| Просмотров | 7470 |
| Номер материала | 625 |