
Презентация "Метод координат в пространстве. Координаты вектора"

Краткое описание документа:
Презентация «Метод координат в пространстве. Координаты вектора» наглядно представляет материал по данной теме для обучения на школьном уроке. В ходе рассмотрения темы даются основные определения, описываются примеры решения задач по теме, наглядно демонстрируются свойства векторов. С помощью данной презентации учителю легче сформировать у учеников представления об изучаемом предмете, научить их решать задачи, где применяются изучаемые положения. Также использование презентации помогает удерживать внимание учеников на изучаемом предмете, повысить эффективность обучения.

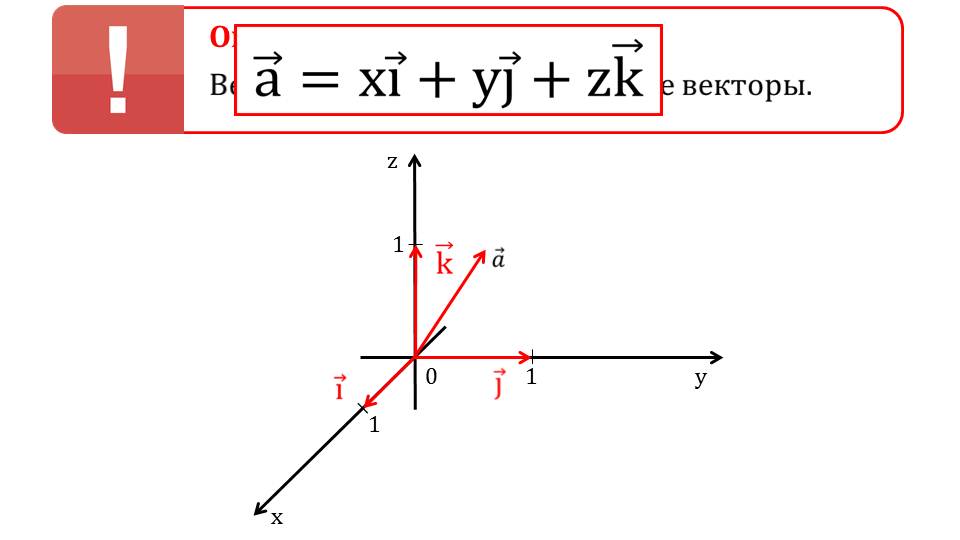
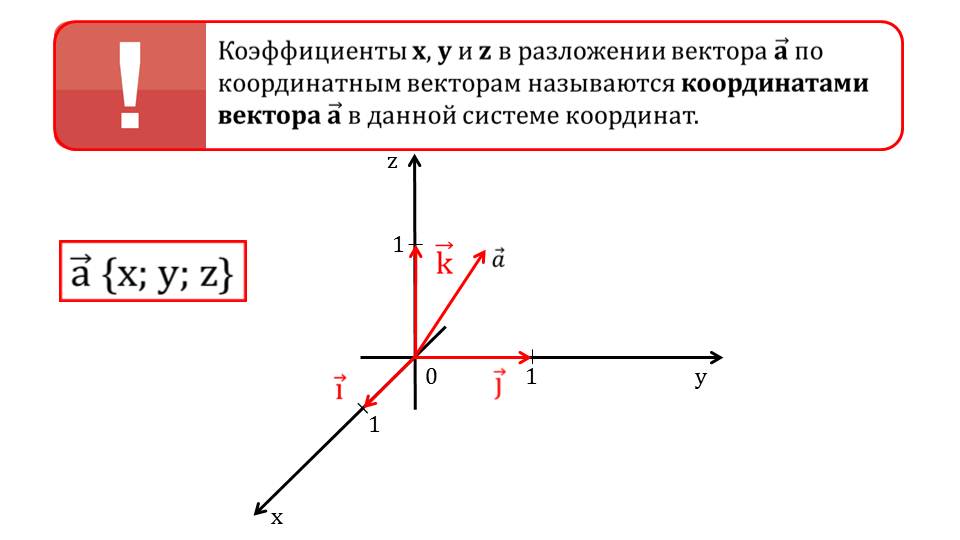
Демонстрация начинается с представления определения компланарных векторов. В рамке выделено, что таким векторами будут называться вектора, которые, начинаясь из одной точки, принадлежат одной плоскости. На втором слайде изображена система координат, на которой отмечены ее координатные векторы iˉ, jˉ, kˉ - единичные векторы, лежащие на осях координат и с направлением, совпадающим с положительным направлением оси. От начала координат проводится вектор aˉ, которых представляет собой сумму координатных векторов, умноженных на некоторые числовые коэффициенты aˉ=хiˉ+уjˉ+zkˉ. Данные числовые коэффициенты в разложении вектора aˉ являются координатами данного вектора в представленной системе координат. Представляется математическая запись координат вектора aˉ{x;y;z}.
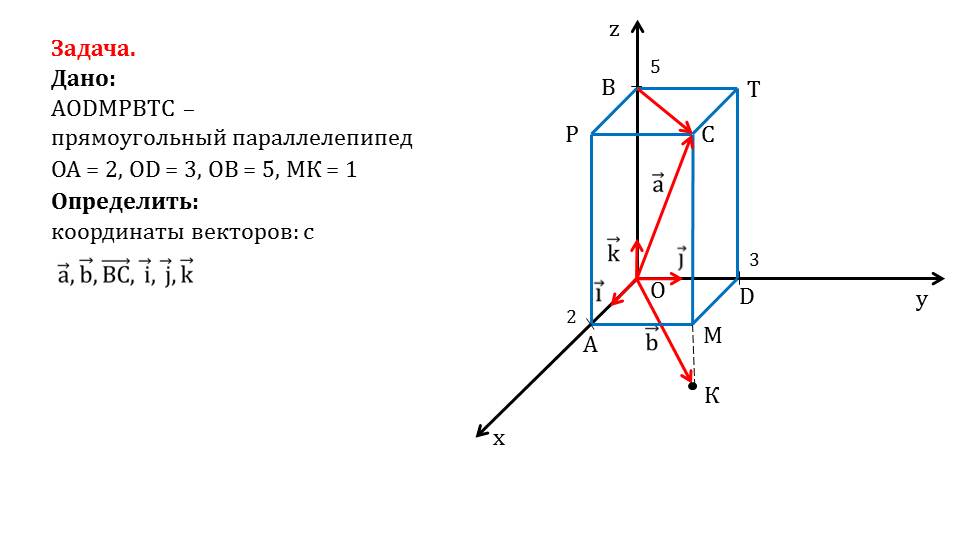
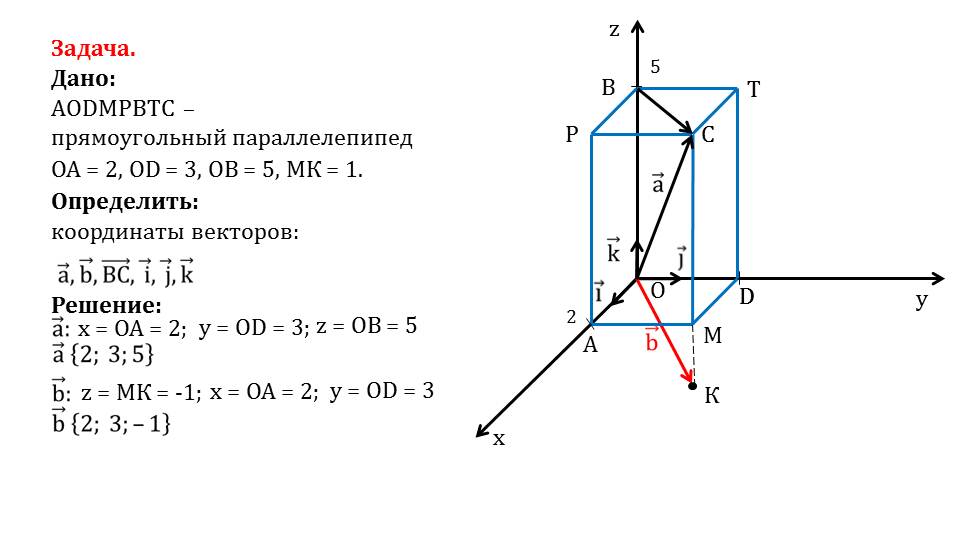
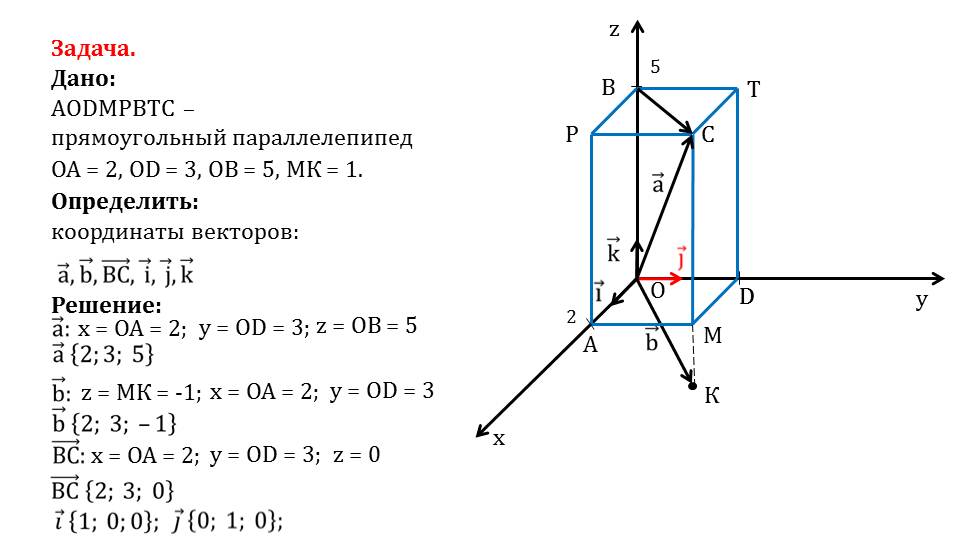
На слайде 4 представлено решение задачи, в которой дан прямоугольный параллелепипед AODMPBTC с известными расстояниями ОА=2, OD=3, OВ=5 и МК=1. Необходимо определить координаты векторов aˉ, bˉ, ВСˉ, iˉ, jˉ, kˉ. На рисунке к решению данной задачи изображается система координат, в которой построен данный параллелепипед. Известны длины сторон параллелепипеда, а также разница между аппликатами точек М и К. необходимо найти координаты вектора ВСˉ - диагонали грани РВТС, диагонали параллелепипеда aˉ и вектора, направленного из начала координат в точку К.
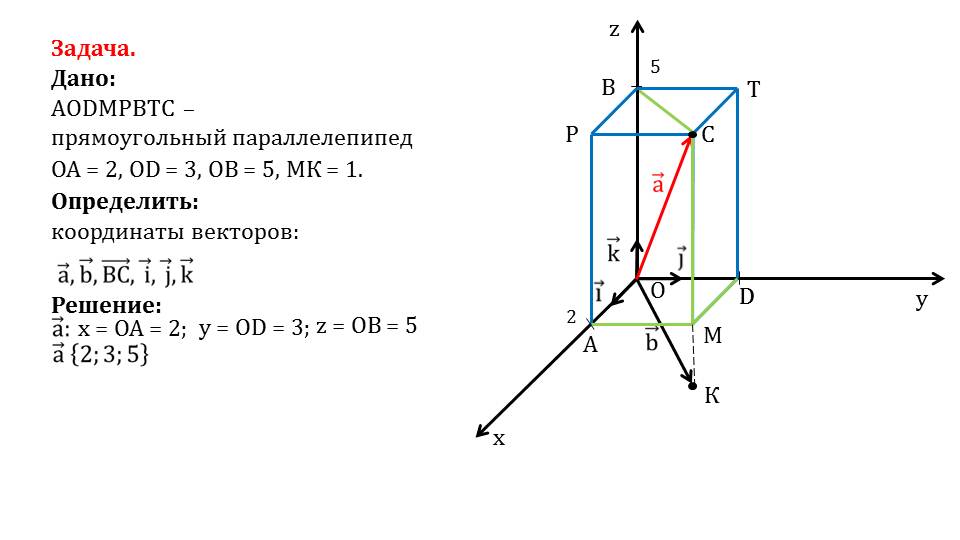
Сначала определяются координаты вектора aˉ. Зная, что аппликата вектора совпадает с ординатой точки В, ордината совпадает с ординатой точки D, а абсцисса вектора совпадает с ОА. Соответственно, координаты вектора aˉ{2;3;5}. На слайде 6 демонстрируется нахождение координат вектора bˉ.
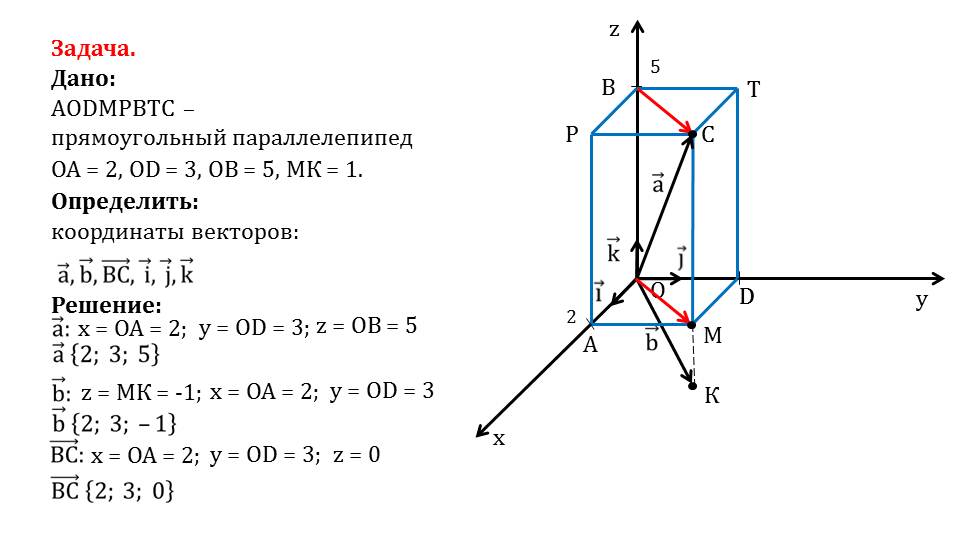
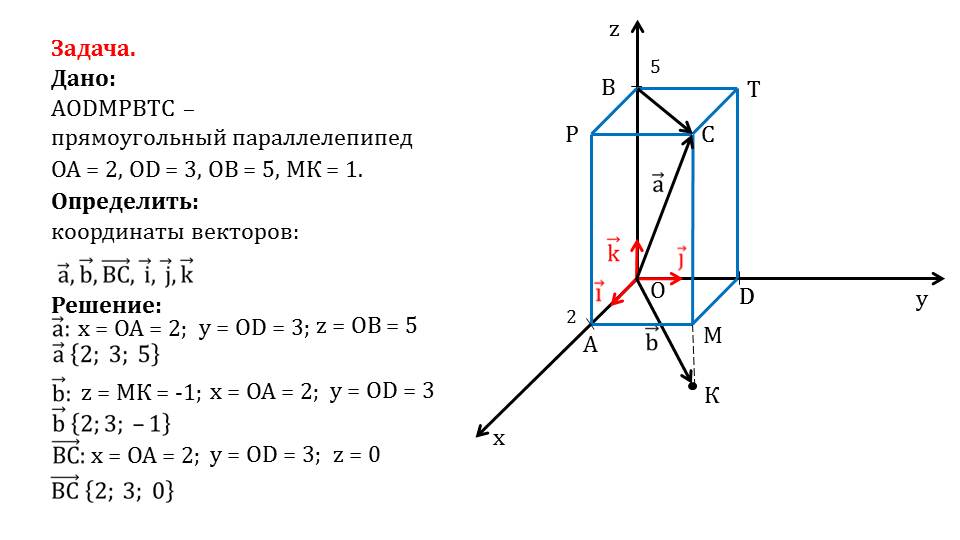
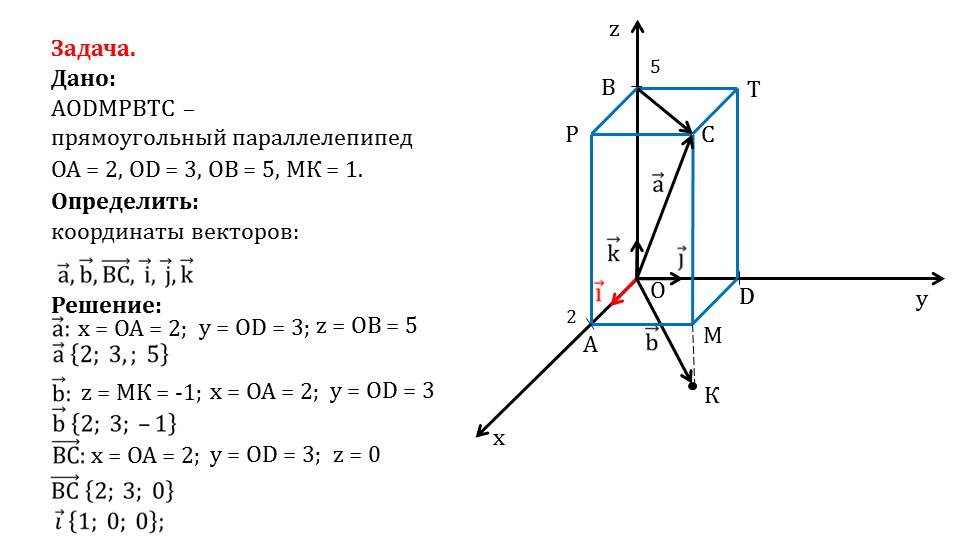
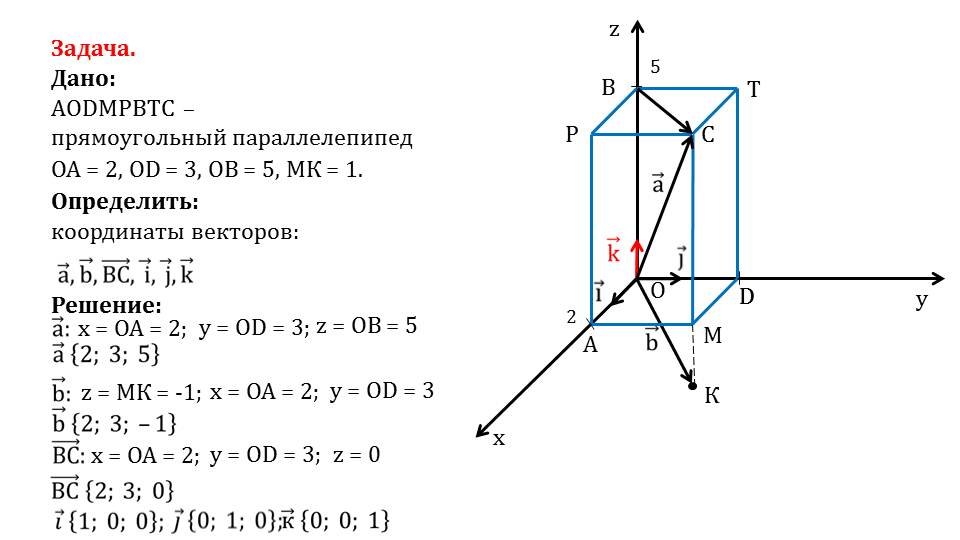
Координаты данного вектора также легко определить, пользуясь свойствами прямоугольного параллелепипеда и известными координатами. Абсцисса вектора равна ОА=2, ордината равна OD=3, а аппликата равна МК с противоположным знаком, то есть bˉ{2;3;-1}. На слайде 7 определяем координаты вектора ВСˉ. Пользуясь свойствами прямоугольного параллелепипеда и координатами известных векторов, находим координаты вектора ВСˉ{2;3;0}. Далее определяются координаты векторов iˉ, jˉ, kˉ. Это единичные векторы, которые лежат на координатных осях. На слайдах 9, 10 и 11 рассматривается определение координат этих векторов. В результате анализа получаем координаты iˉ{1;0;0}, jˉ{0;1;0}, kˉ{0;0;1}. Задача решена.
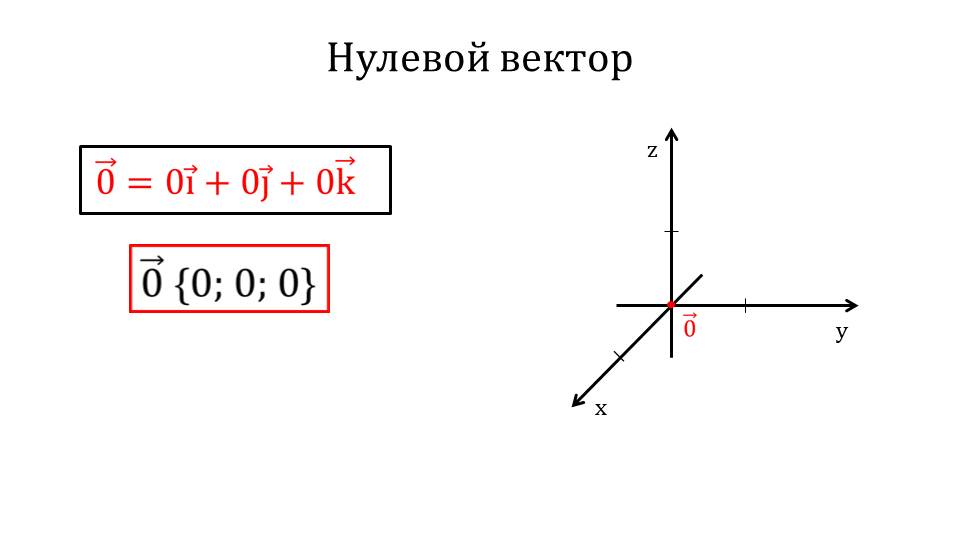
На слайде 12 рассматривается нулевой вектор. Дано его изображение в системе координат, а также разложение по координатным векторам 0ˉ=0iˉ+0jˉ+0kˉ. Соответственно, координаты нулевого вектора 0ˉ{0;0;0}.
Далее описываются свойства векторов, разложенных по координатам. На слайде 13 представлено свойство равных векторов. Отмечено, что координаты таких векторов соответственно равны. Свойство объясняется на примере векторов aˉ{x1;y1;z1}=bˉ{x2;y2;z2}. Отмечается, что у этих векторов x1=x2, у1=у2, z1=z2.
На слайде 14 представлено свойство координат суммы векторов. В рамку выделено правило, что координаты суммарного вектора равны сумме соответствующих координат складываемых векторов. Свойства также описывается с помощью векторов aˉ{x1;y1;z1} и bˉ{x2;y2;z2}. Отмечается, что aˉ+ bˉ={x1+ x2;y1+ y2;z1+z2}.
Слайд 15 представляет свойство разности векторов. В рамке для запоминания выделено правило. Что координаты разности векторов определяются разностью соответствующих координат векторов, участвующих в разности. Следовательно, для векторов aˉ{x1;y1;z1} и bˉ{x2;y2;z2} будет верно равенство aˉ-bˉ={x1-x2;y1-y2;z1-z2}.


Нахождение координат вектора, умноженного на некоторое число, описывается на слайде 16. Выделено правило нахождения координат результирующего вектора о том, что каждая координата данного вектора умножается на данное число. Приводится пример для вектора aˉ{x1;y1;z1}.
Отмечено, что координаты вектора αaˉ, где α – некоторое число координаты вектора αaˉ={αx1;αy1;αz1}.


На слайде 17 описывается решение задачи, в которой даны три вектора aˉ{1;-2;0} и bˉ{0;3;-6}, сˉ{-2;3;1}, и необходимо найти вектор pˉ=2aˉ-(1/3)bˉ+cˉ. В соответствии с изученными правилами, находятся координаты результирующего вектора. Сначала определяются вектор 2aˉ{2*1;2*(-2);2*0} и вектор (1/3) bˉ{(1/3)*0; (1/3)*3; (1/3)*(-6)}. Затем находятся разность и сумма соответствующих координат х=0, у=-2, z=3.
Последний слайд демонстрирует решение задачи 2, в которой даны векторы aˉ=3iˉ+2jˉ-5kˉ, bˉ=-5iˉ+3jˉ-kˉ, cˉ=iˉ-jˉ, dˉ=jˉ+kˉ, mˉ=kˉ-iˉ, nˉ=0,7kˉ.
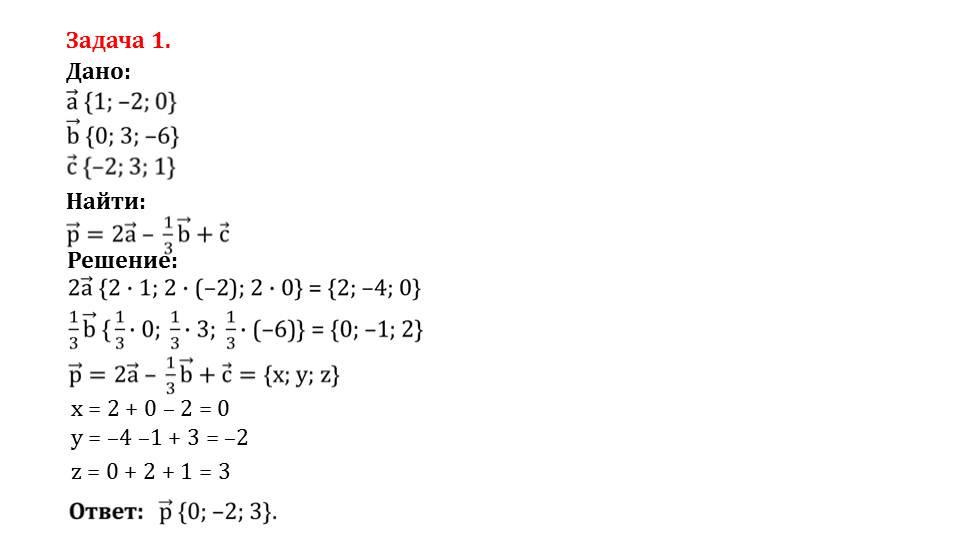

Презентация «Метод координат в пространстве. Координаты вектора» может применяться для обеспечения наглядности обучения на традиционном школьном уроке. Также материал может помочь ученикам, недостаточно хорошо освоившим материал, при самостоятельном изучении. При рассмотрении материала в ходе дистанционного обучения презентация может быть полезна для формирования представления ученика об изучаемом предмете.
| Автор | |
|---|---|
| Дата добавления | 07.11.2014 |
| Раздел | Геометрия |
| Подраздел | Презентация |
| Просмотров | 6845 |
| Номер материала | 958 |