
Презентация "Метод координат в пространстве. Прямоугольная система координат"

Краткое описание документа:
Презентация «Метод координат в пространстве. Прямоугольная система координат» - инструмент наглядного представления материала, который помогает повысить эффективность урока математики по данной теме. В ходе презентации формируется представление учеников о методе координат, детально рассматривается прямоугольная система координат, решение задач с использованием данного метода. Презентация помогает более ярко, наглядно представить изучаемый предмет, удерживать внимание учеников, внося разнообразие в учебный процесс.
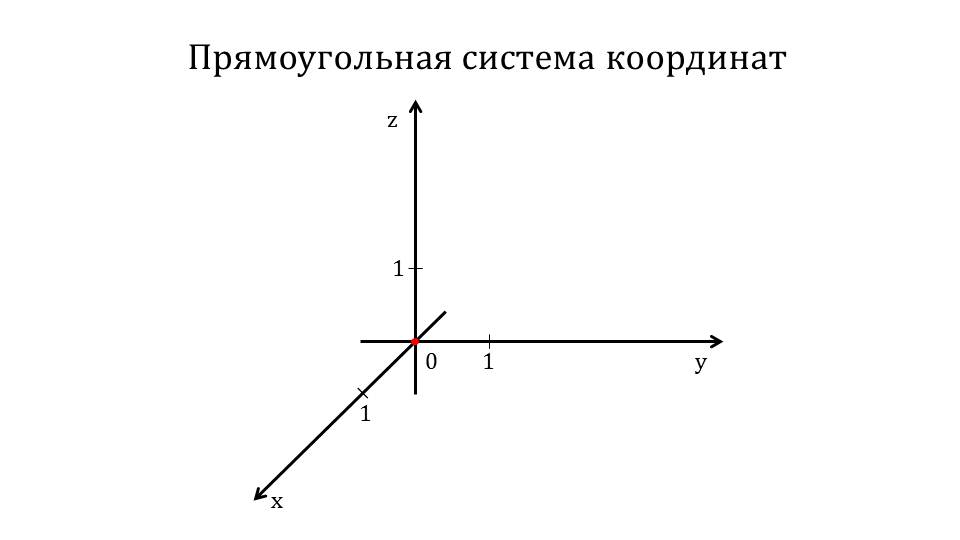
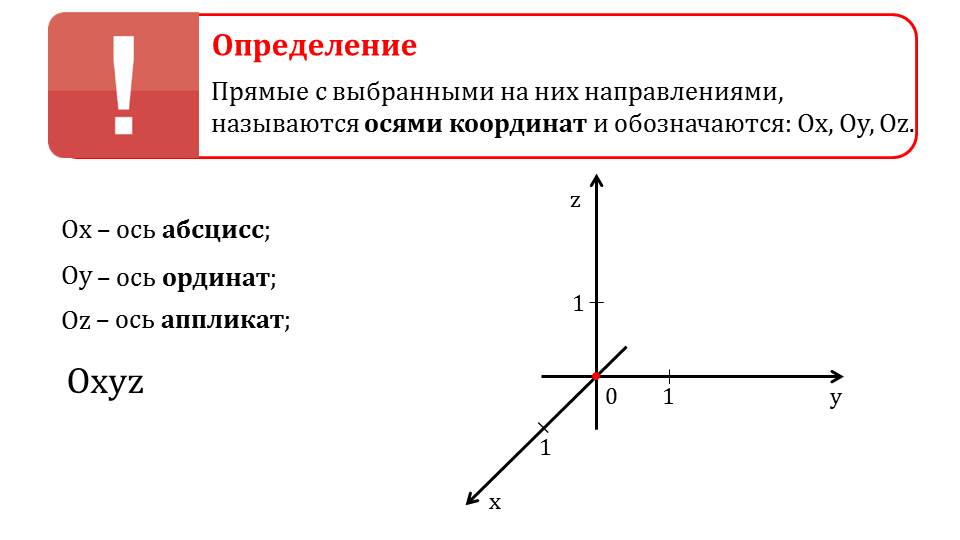
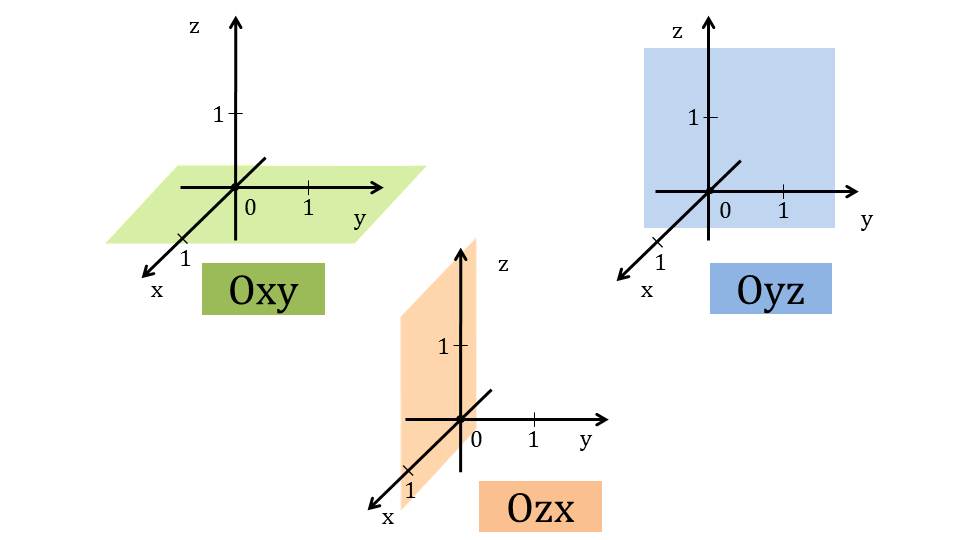
Демонстрация начинается с представления темы и изображения в пространстве прямоугольной системы координат. На первом слайде чертятся три оси системы координат Ох, Оу и Oz. На каждой оси от начала координат отмечается единичный отрезок. Можно отметить, что в дальнейшем координаты объектов будут измеряться количеством представленных единичных отрезков для данного координатного пространства. Представлено определение осей координат как прямых с выбранными направлениями. На слайде 2 отмечается обозначение координатного пространства Oxyz и название осей: Ох – ось абсцисс, Оу –ординат, Oz – аппликат. На третьем слайде выделяются координатные плоскости, образуемые осями координат. На первом рисунке в системе координат выделены оси Ох и Оу, которые принадлежат плоскости Оху, закрашенной зеленым цветом. На втором рисунке выделена координатная плоскость Oyz, которую образуют координатные оси Oy и Oz. Третий рисунок демонстрирует закрашенную бежевым цветом координатную плоскость Oxz, образованную осями Ox и Oz.
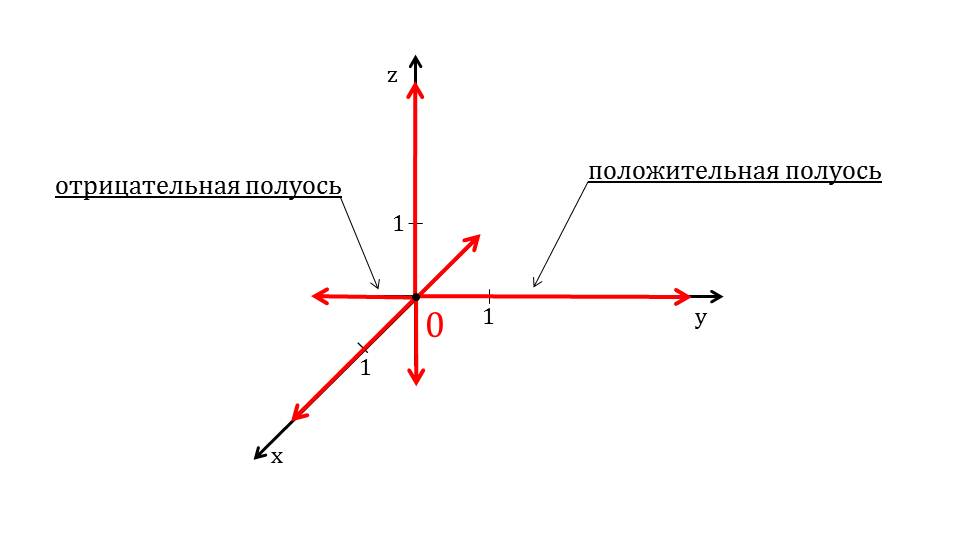
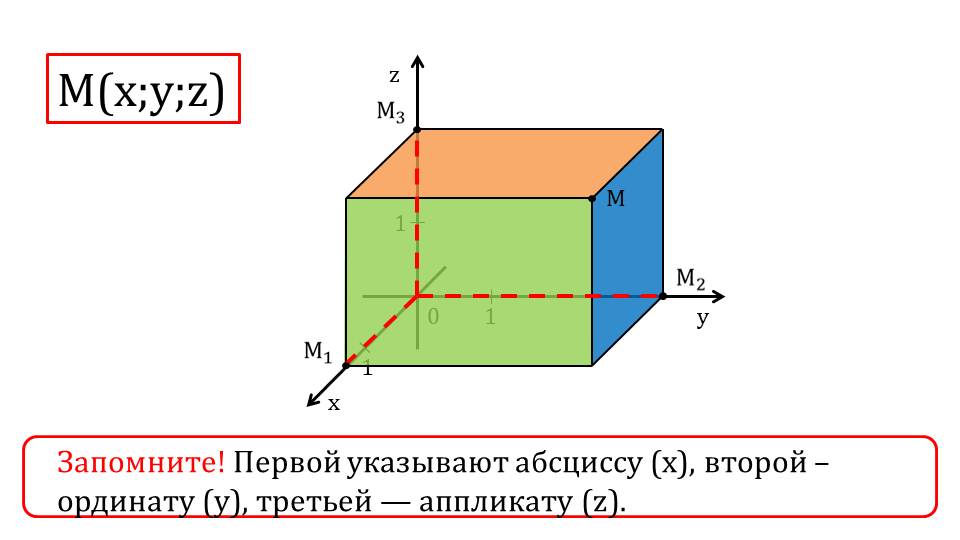
Более подробно рассматривается направление осей координат на слайде 4. В каждой из осей заданное при построении направление отмечается как положительное. При этом вторая полуось оси, направленная от центра координат в сторону, обратную положительному направлению, задает отрицательное направление. С помощью указателей и выделения красным цветом отмечаются положительные и отрицательные полуоси каждой оси системы координат. Далее рассматривается порядок обозначения координат в математической записи. На слайде 5 изображена система координат Oxyz, на которой отмечена точка М(x;y;z). От точки М на каждую из координатных плоскостей опускается перпендикуляр. Образованные перпендикулярами плоскости, параллельные координатным плоскостям, окрашены в различные цвета. Полученные при построении точки, принадлежащие осям координат, обозначены М1, М2, М3. Под рисунком указано правило, согласно которому записываются координаты – сначала абсцисса, затем ордината и аппликата.
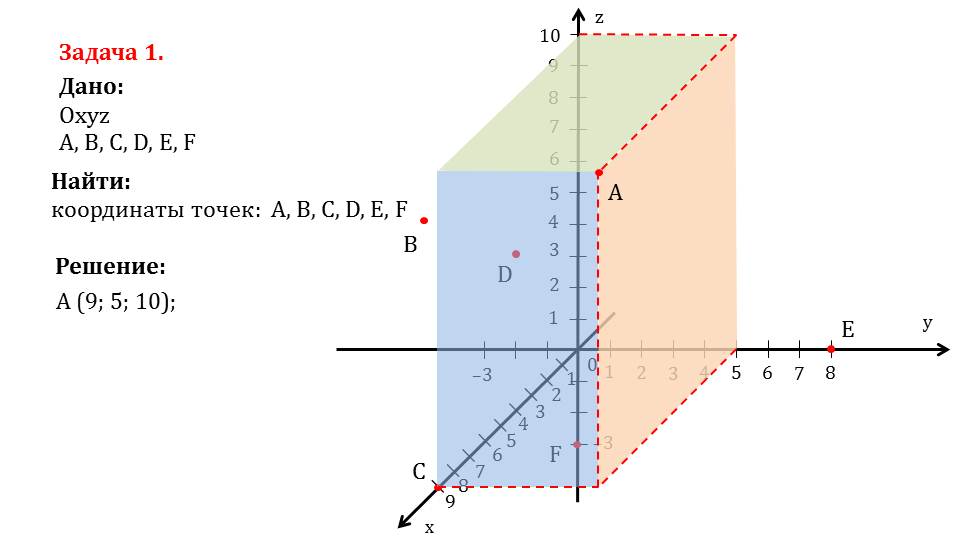
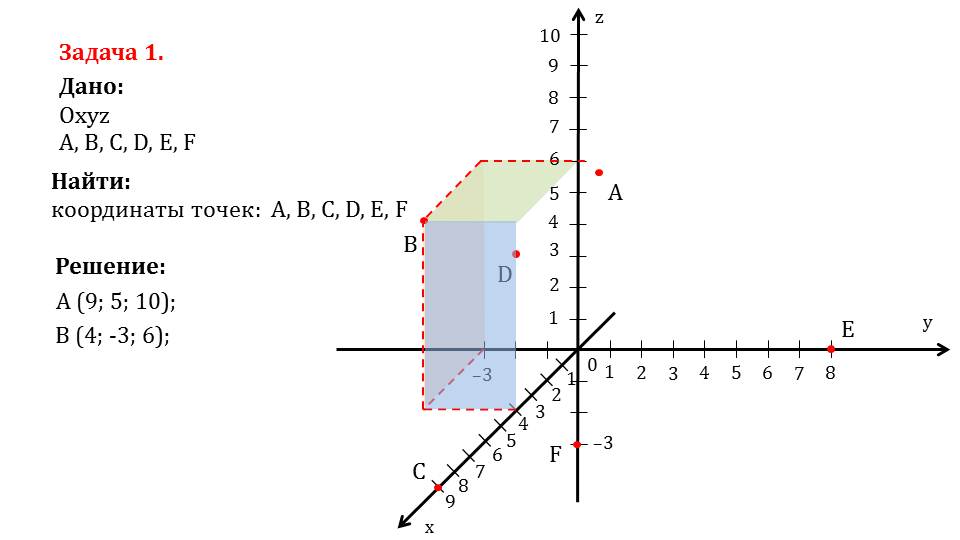
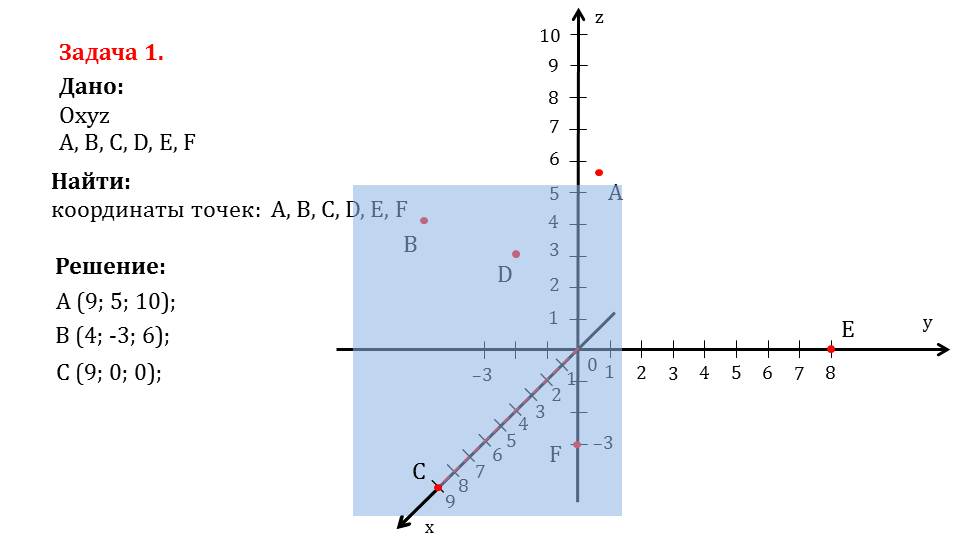
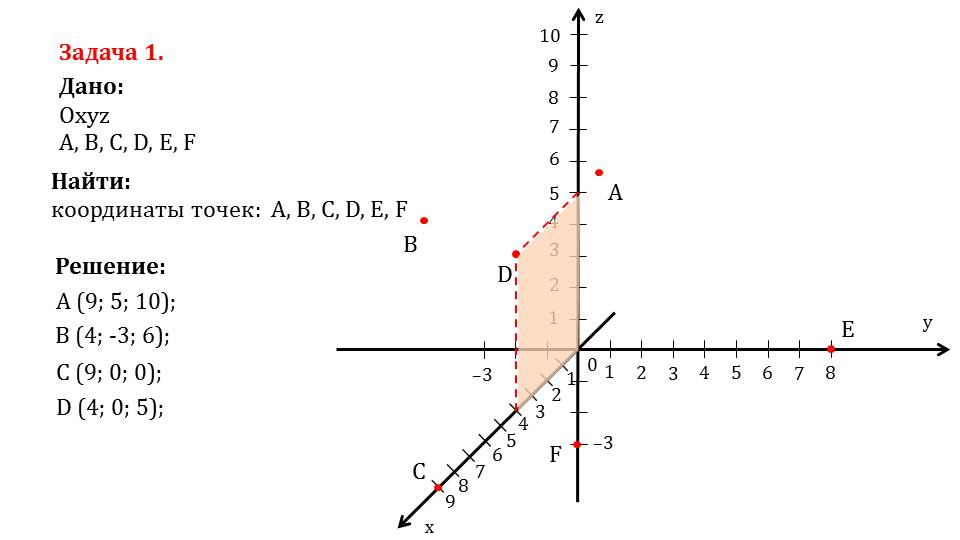
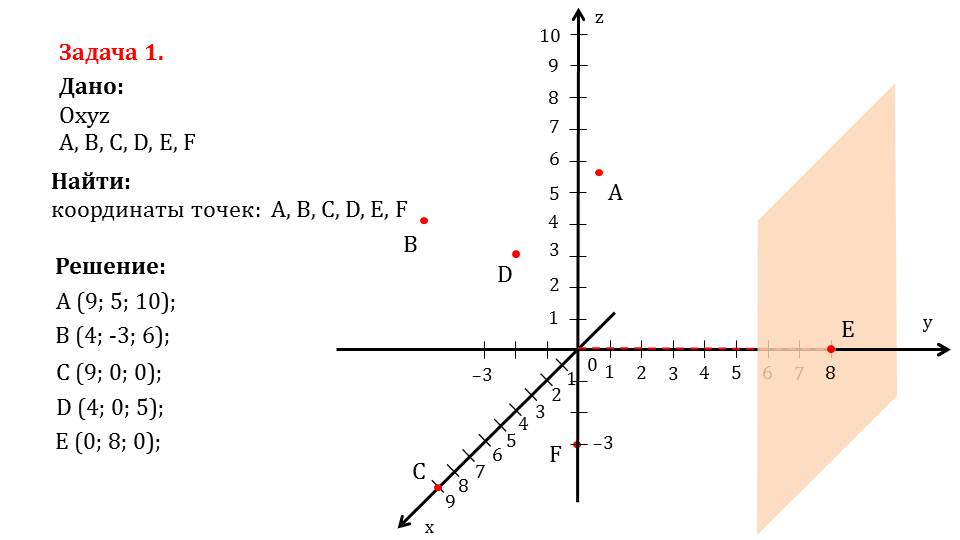
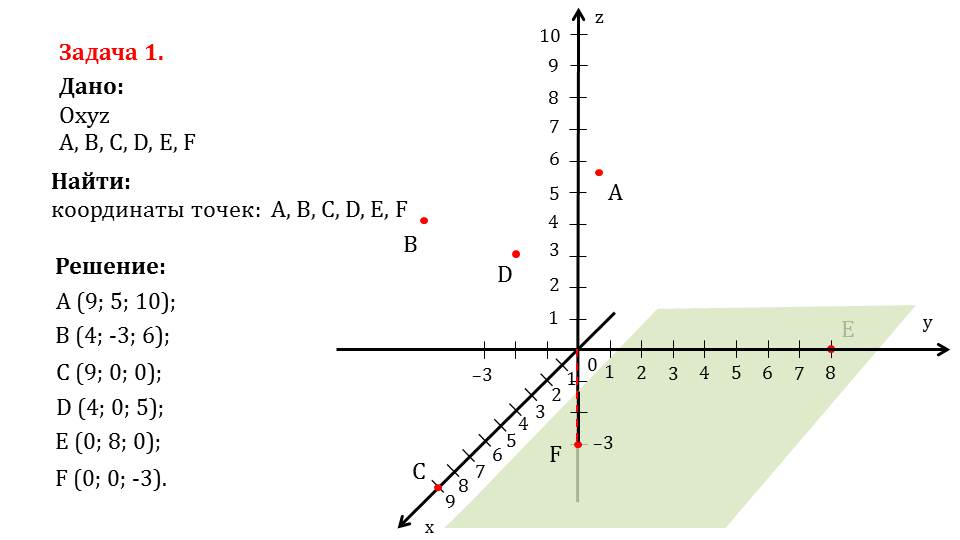
На слайде 6 рассматривается решение задачи 1, в которой необходимо найти координаты отмеченных шести точек. Сначала определяются координаты точки А, от которой проводятся перпендикуляры к каждой координатной плоскости. В результате построения точки пересечения каждой плоскости с осями координат и будут являться координатами данной точки. Построенные соответствующие плоскости, образованные перпендикулярами, окрашены различными цветами, на осях координат отмечены значения координат точки. Таким образом находятся координаты А(9;5;10). На следующем слайде построены и окрашены разными цветами плоскости, образуемые перпендикулярами, проведенными от данной точки к координатным плоскостям. Так находятся координаты точки В(4;-3;6). Точка С лежит на оси Ох, поэтому ее координаты С(9;0;0). На слайде 9 определяются координаты точки D. Так как при проведении перпендикуляров от нее к координатным плоскостям обнаруживается, что она лежит на координатной плоскости Oxz, то координата у нулевая, то есть D(4;0;5). Аналогично определяются координаты точки E(0;8;0) и F(0;0;3).
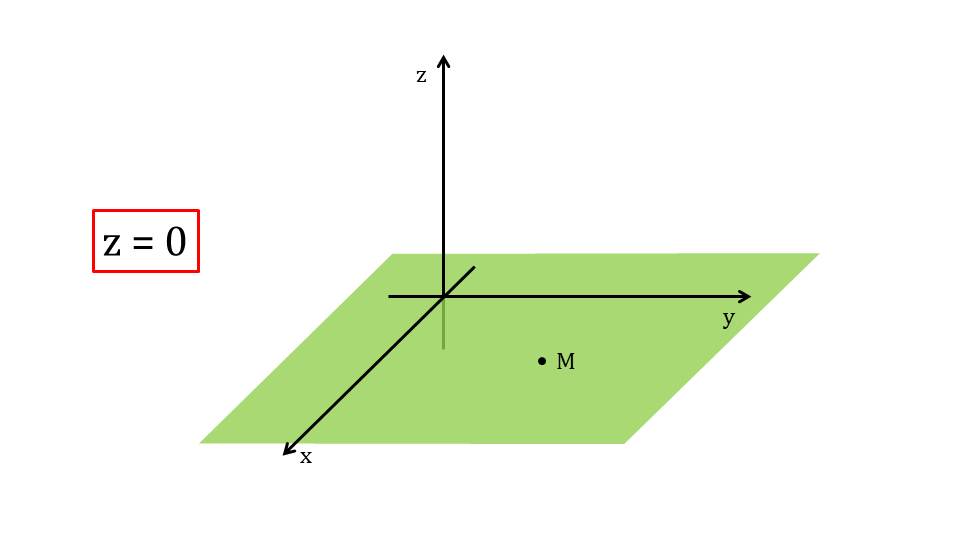
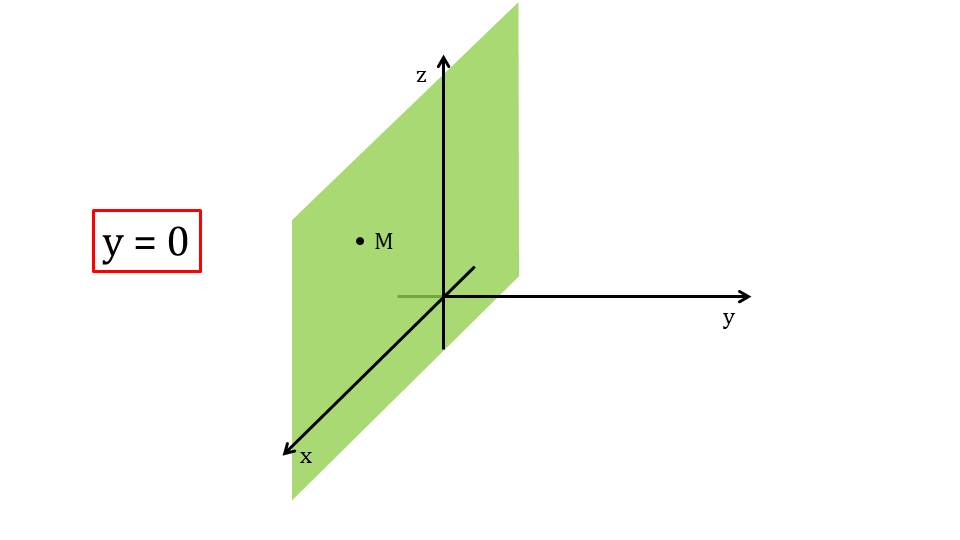
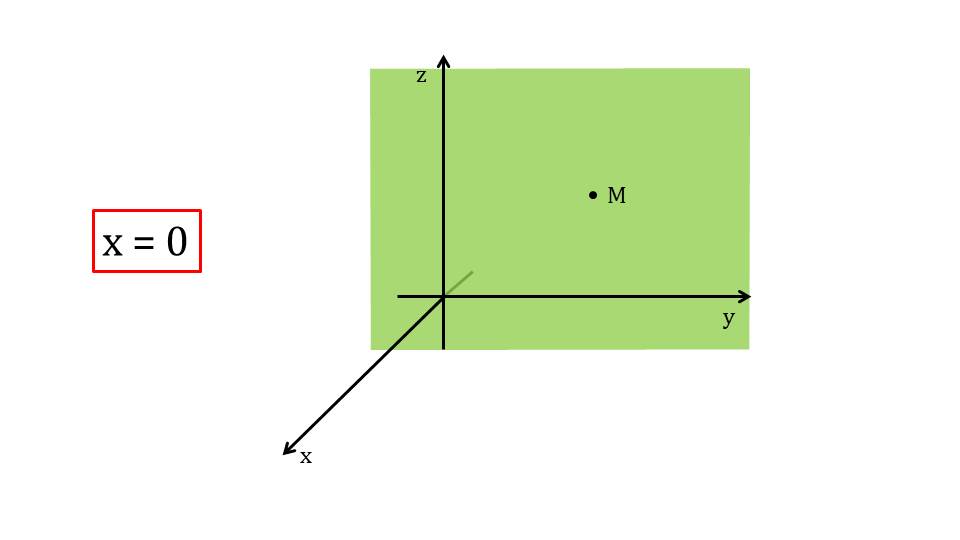
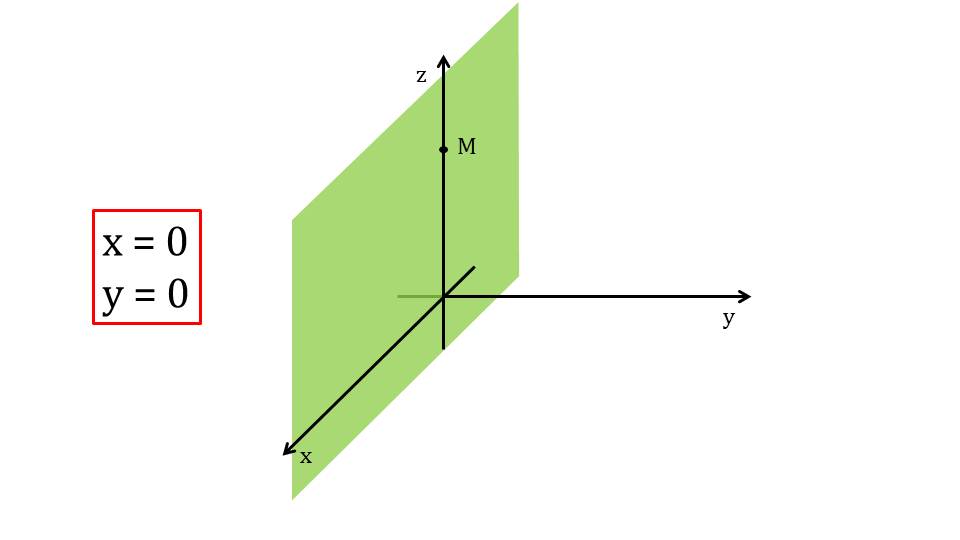
Обобщая рассмотренные примеры, на слайде 12 отмечается, что любая точка М, которая лежит на координатной плоскости Оху имеет нулевую аппликату z=0. Аналогично на слайде 13 определяется нулевая ордината у=0 точки, лежащей на координатной плоскости Oxz. А также на слайде 14 рассматривается нулевая абсцисса точки М, лежащей на координатной плоскости Oyz.
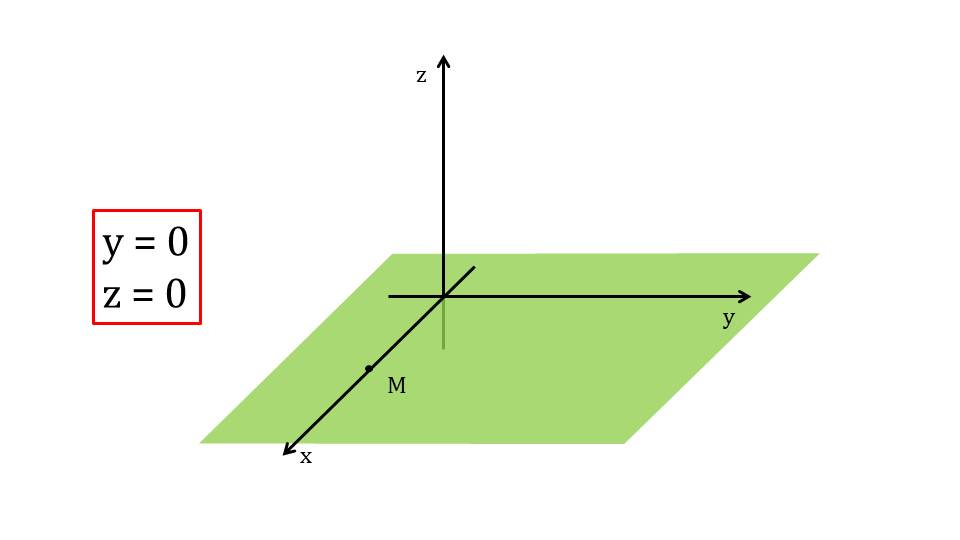
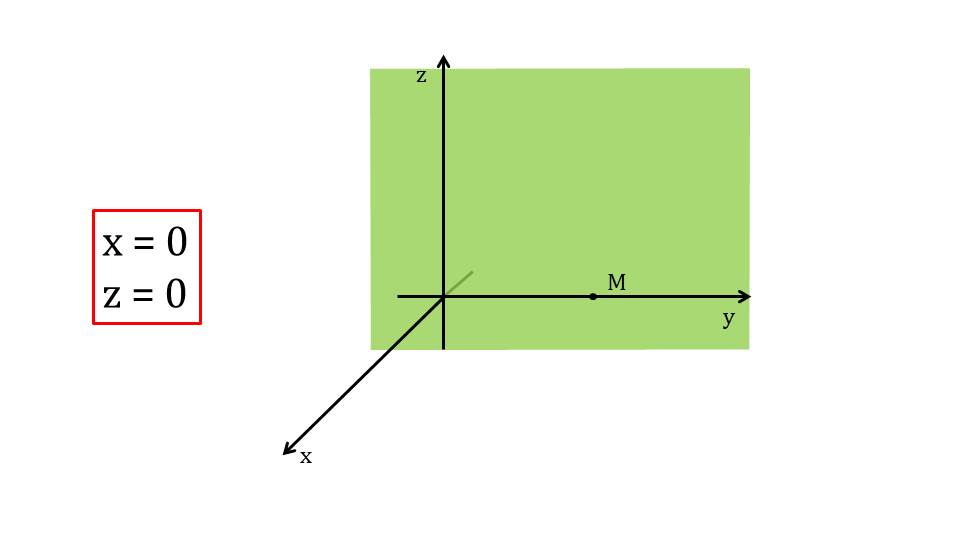
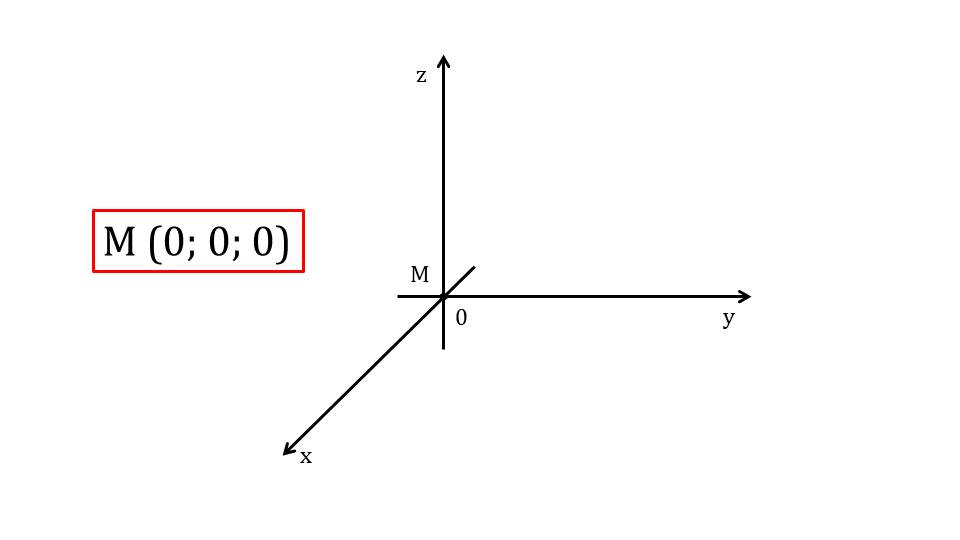
Далее обобщаются в правила примеры определения координат точек, лежащих на координатных осях. На слайде 15 приводится пример точки М, лежащей на координатной оси Ох. Ордината и аппликата точки нулевые у=0 и z=0. На слайде 16 изображается точка М, лежащая на координатной оси Оу. Ее абсцисса и аппликата равны нулю х=0 и z=0. На слайде 17 аналогично рассматривается точка М, лежащая на оси Оz. Ее абсцисса и ордината нулевые. Отдельно на слайде 18 обращается внимание учеников на координаты начала координат точки М(0;0;0).
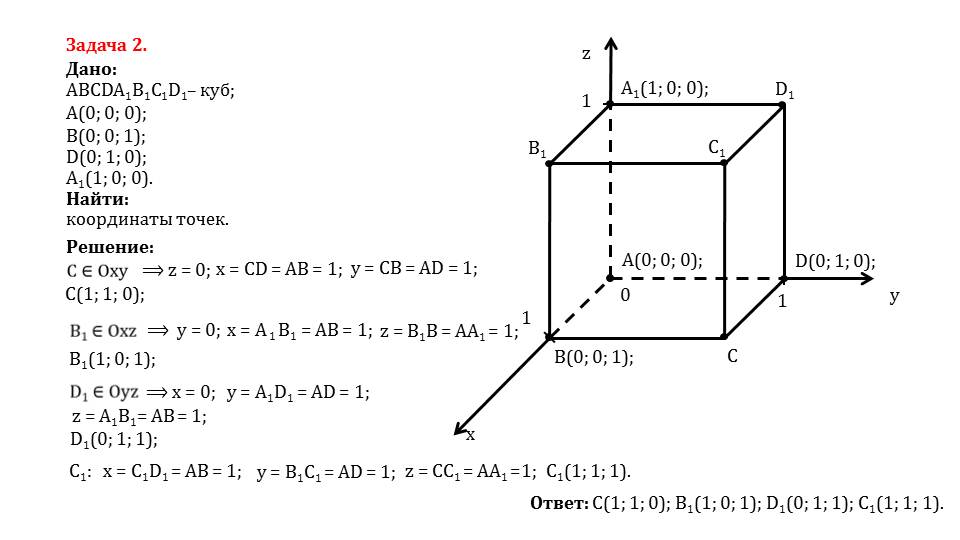
На слайде 19 представлено решение задачи, в которой дан куб ABCDA1B1C1D1. Даны координаты нескольких вершин куба A(0;0;0), B(0;0;1), D(0;1;0), A1(1;0;0). Необходимо найти координаты оставшихся вершин. На рисунке, сопровождающем решение задачи, в системе координат изображен куб. Из построения видно, что Точка А лежит в начале координат, В – на оси Ох, D – на оси Оу, а А1 – на оси аппликат. Из свойств куба можно определить, что точка С принадлежит координатной плоскости Оху, а значит ее аппликата нулевая. Из равенства ребер куба следует, что координаты х=1 и у=1. Следовательно, координаты точки С(1;1;0). Также можно определить, что точка B1 принадлежит координатной плоскости Oxz, поэтому ее ордината нулевая у=0. Из равенства ребер куба следует х=1 и z=1. Найденные координаты точки B1(1;0;1) Точка D1 лежит в координатной плоскости Oyz, поэтому ее абсцисса нулевая х=0. Из равенства ребер куба следует у=1 и z=1. Найденные координаты D1(0;1;1).
Пользуясь свойством куба равенства его ребер, находим координаты точки С1(1;1;1). Задача решена.
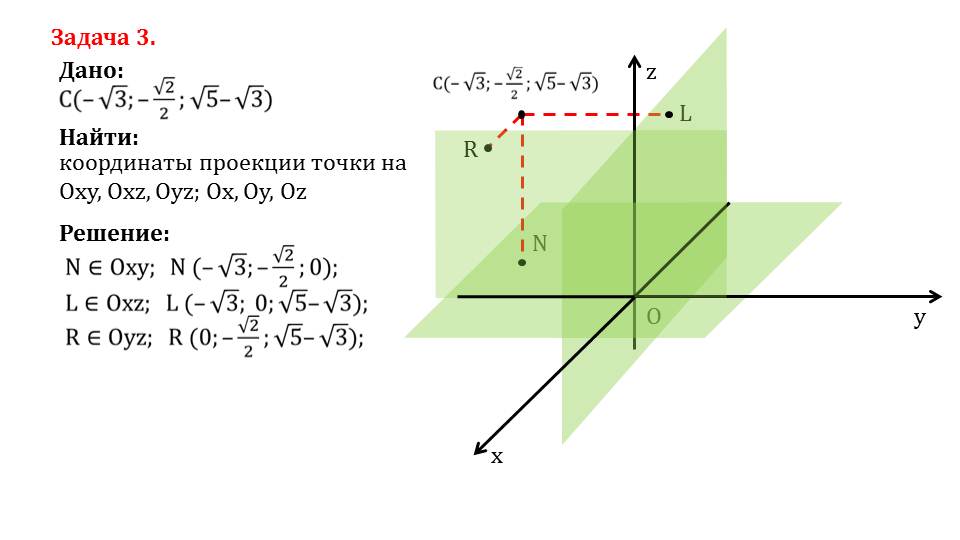
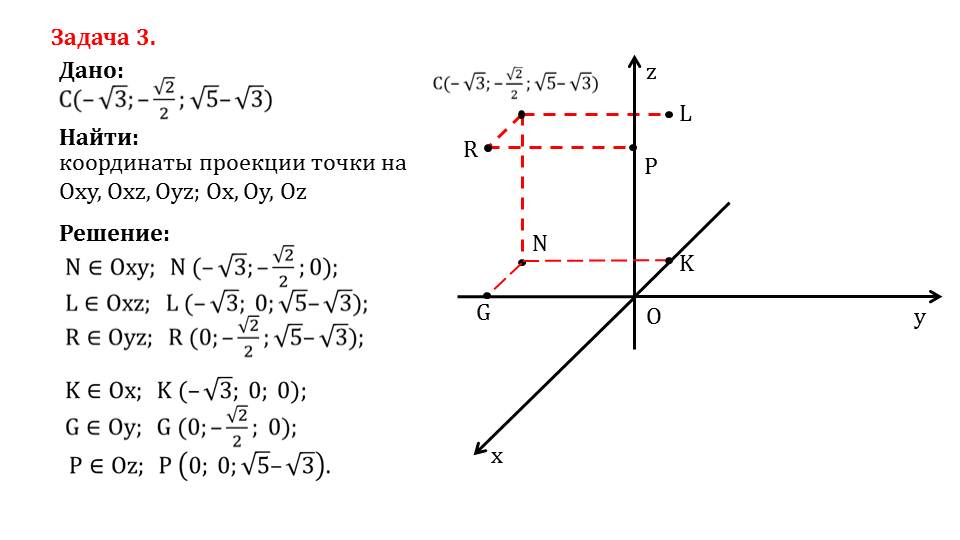
На слайде 3 рассматривается решение задачи, в которой необходимо найти координаты проекций точки С(-√3;-√2/2;-√5-√3) на все координатные плоскости и координатные оси. На рисунке к решению данной задачи изображается система координат, построена точка С, проведены от нее перпендикуляры к координатным плоскостям. Перпендикуляры пересекают координатные плоскости в точках R, L, N. В ходе рассмотрения построенных проекций определяются их координаты. Так как N принадлежит координатной плоскости Оху, то ее координаты N(-√3;-√2/2;0). Проекция L, лежащая на плоскости Oxz, имеет координаты L(-√3;0;-√5-√3), а проекция на координатную плоскость Oyz имеет координаты R(0;-√2/2;-√5-√3).
Аналогично решается задача о нахождении координат проекций точки на все оси координат. На рисунке слайда 21 от точки проводятся перпендикуляры к осиям координат, определяются координаты соответствующих точек, являющихся проекциями точки С: K(-√3;0;0), G(0;-√2/2;0), P(0;0;-√5-√3). Задача решена.
Презентация «Метод координат в пространстве. Прямоугольная система координат» применяется для повышения эффективности традиционного школьного урока. Также материал может быть полезен учителю, осуществляющему обучение дистанционно. При необходимости углубить знания ученика по предмету, ему может рекомендоваться презентация для самостоятельного рассмотрения.
| Автор | |
|---|---|
| Дата добавления | 07.11.2014 |
| Раздел | Геометрия |
| Подраздел | Презентация |
| Просмотров | 13147 |
| Номер материала | 957 |