
Презентация "Метод координат в пространстве. Вычисление углов между прямыми и плоскостями"

Краткое описание документа:
Презентация «Метод координат в пространстве. Вычисление углов между прямыми и плоскостями» наглядно представляет материал по данной теме. С помощью видеоурока учителю легче сформировать представление об углах между прямыми и плоскостями в пространстве, научить их находить, используя изученные теоретические сведения.
Геометрические объекты в пространстве сложно демонстрировать на классной доске. Использование презентации необходимо, чтобы ученикам было легче представить рассматриваемые объекты. Линии чертежей видны на слайдах более четко, с любой парты в классе. Анимация помогает демонстрировать материал последовательно, выделяя важные моменты и особенности построения. Использование красочного наглядного материала – эффективный прием для удержания внимания учеников на обучении. В ходе презентации рассматривается понятие направляющего вектора, описываются решения задач, в которых требуется найти угол между данными векторами.
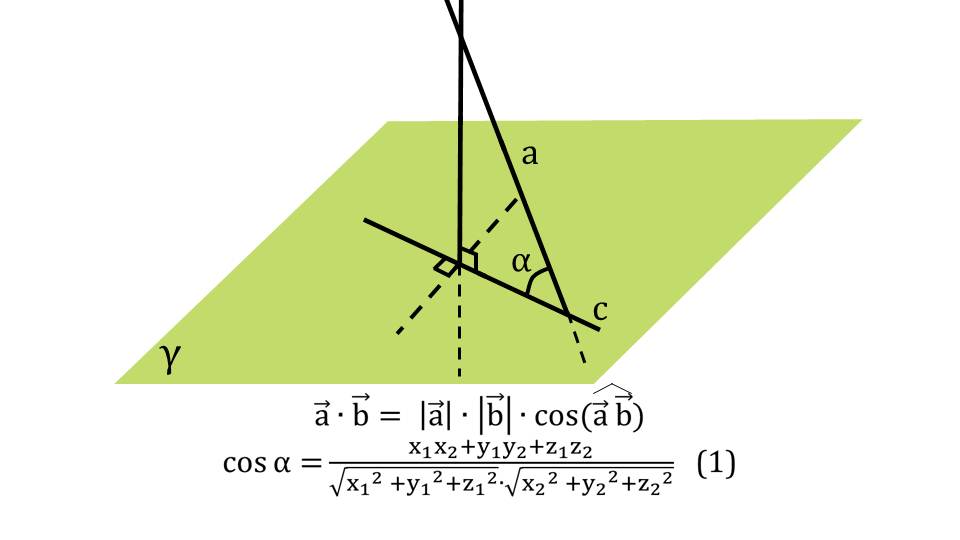
Презентация начинается с напоминания теоретического материала о векторах и углах между ними. На рисунке изображается плоскость γ, которую пересекает прямая а. От этой прямой к плоскости проведен перпендикуляр. Соединение точки пересечения перпендикуляра и плоскости γ с точкой пересечения прямой а и плоскости γ принадлежит прямой с. Угол α между прямой а и прямой с является углом между прямой а и плоскостью γ. Ниже иллюстрации напоминается формула произведения векторов a¯b¯=|a¯|·|b¯|·cos(a¯^b¯) и cosα=x1x2/√( x12+y12+z12)·√( x22+y22+z22).
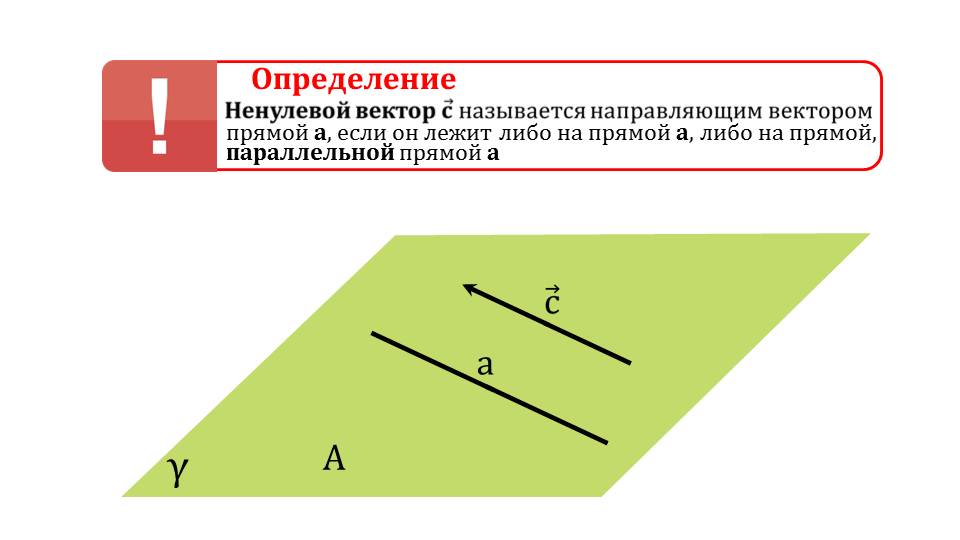
На втором слайде демонстрируется определение направляющего вектора некоторой прямой а. Отмечается, что это ненулевой вектор, который лежит либо на самой прямой, либо на параллельной ей. Определение иллюстрировано расположенным ниже него рисунком. На рисунке изображена плоскость γ, на которой лежит прямая а и вектор с¯, лежащий на параллельной ей прямой.
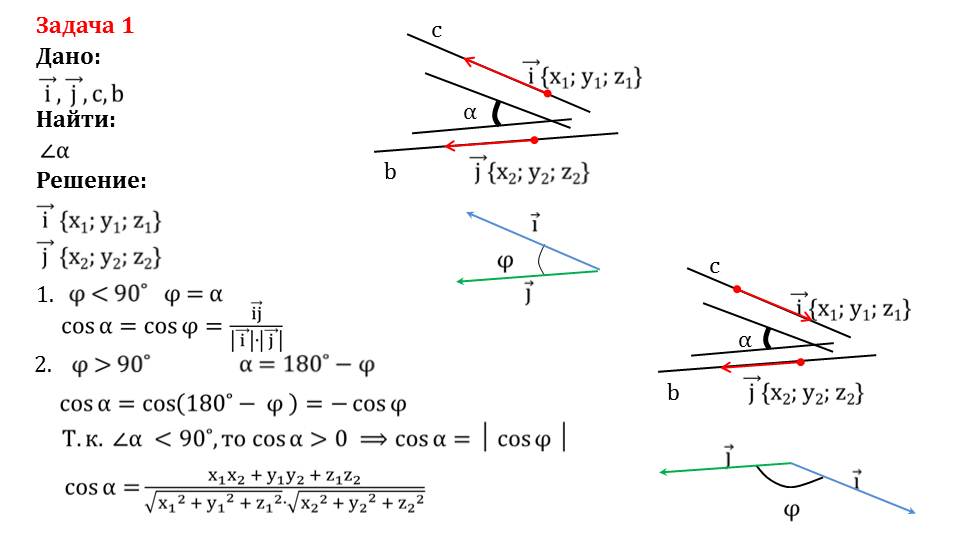
Далее рассматривается решение задач, в которой даны четыре вектора i¯, j¯, c¯, b¯. Векторы изображены на рисунке. Необходимо найти угол между векторами. Чтобы решить задачу, отмечаются координаты векторов i¯{x1;y1;z1} и j¯{x2;y2;z2}. Рассматриваются два возможных случая. В первом – угол между векторами i¯, j¯ острый, то есть φ<90°. В этом случае углы φ и α совпадают, их легко найти с помощью известной формулы для нахождения косинуса, то есть cosα= cosφ= i¯j¯/|i¯|·|j¯|. Во втором случае рассматривается тупой угол φ>90°. Тогда α=180°-φ. Соответственно, косинус угла cosα= cos(180°-α)=- cosφ. Так как угол α острый, то его косинус больше нуля, cosα= |cosφ|. А косинус находится по формуле cosα=x1x2/√( x12+y12+z12)·√( x22+y22+z22).

На слайде 4 необходимо вычислить углы между векторами с данными координатами. Даны две пары векторов a¯{2;-2;0} и b¯{4;0;-4}, а также а¯{-3;-3;0} и b¯{√2;√2;2}. Используя известные формулы вычисления косинуса угла, образующегося двумя векторами, после подстановки в эти формулы координат векторов, определяется косинус угла. Зная значение косинуса угла, можно найти величину угла. В первом случае cos(a¯^b¯)=1/2, то есть a¯^b¯=60°. Во втором случае cos(a¯^b¯)=-√2/2, то есть a¯^b¯=180°-45°=135°.
На слайде 5 описывается решение примера 2, в котором требуется вычислить угол между векторами KP¯ и KN¯. Даны координаты начальной и конечной точек векторов. Пользуясь формулой для вычисления координат вектора, которые определяются разностью начальных и конечных соответствующих координат. Затем, имея координаты векторов, по изученной формуле определяется косинус угла. В соответствии с найденным косинусом, определяется величина угла. Найденная величина угла KP¯^KN¯=60°.

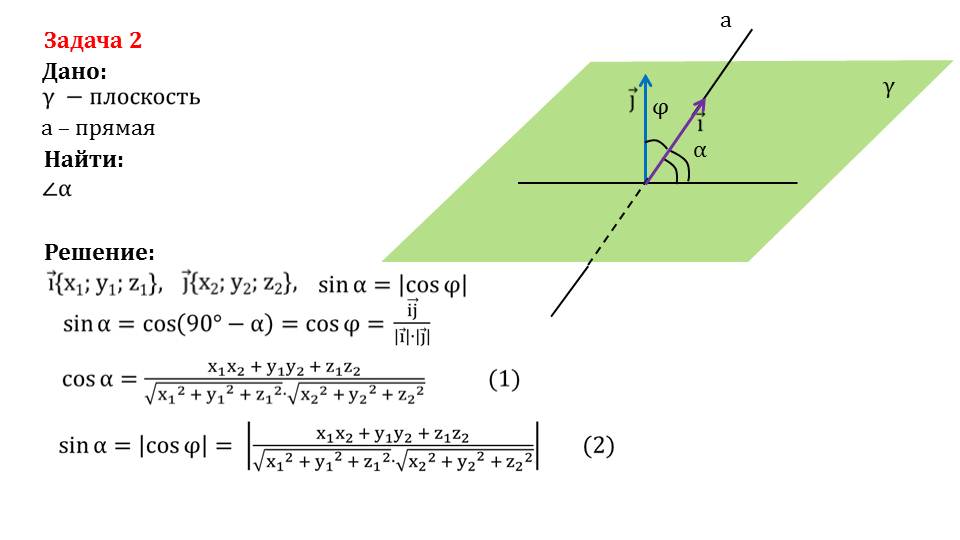
На слайде 6 описывается решение задачи 2, в которой нужно найти угол α между прямой а и плоскостью φ. Задача сопровождается рисунком, на котором изображена плоскость γ, которую пересекает прямая а. В точке пересечения прямой плоскости проводится перпендикуляр к плоскости. Откладываются из точки пересечения прямой и плоскости векторы i¯{x1;y1;z1} и j¯{x2;y2;z2}. Отмечается, что синус угла между векторами равен модулю косинуса угла между прямой а и плоскостью γ. Из построения видно, что sinα=cos(90°-α)=cosφ= i¯j¯/|i¯|·|j¯|. Зная формулу для определения косинуса угла между векторами, находим sinα=|cosφ|=| x1x2/√( x12+y12+z12)·√( x22+y22+z22)|.
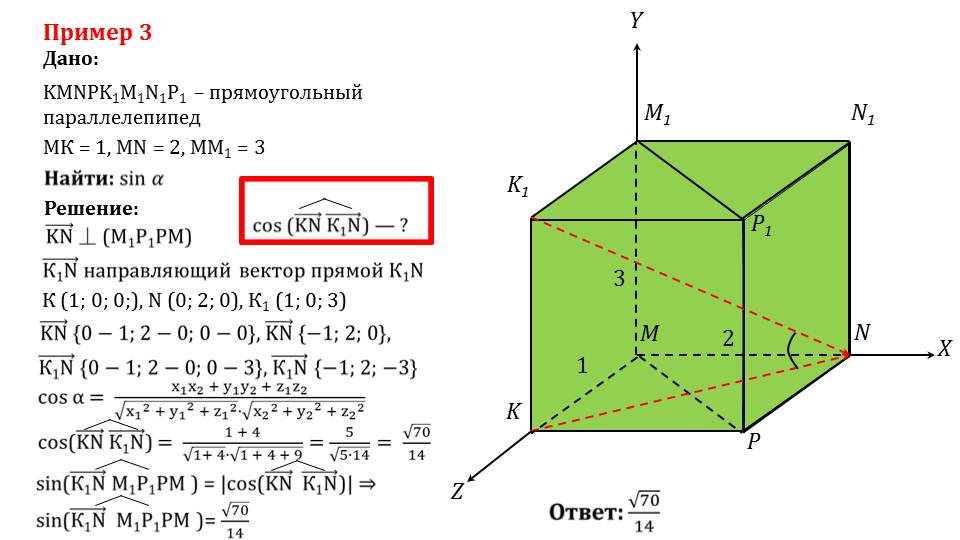
В последнем слайде описан пример, в котором необходимо найти синус угла между диагональю основания и диагональю прямоугольного параллелепипеда со сторонами MK=1, MN=2, MM1=3. Отмечается, что иначе нужно найти косинус угла между векторами KN¯ и K1N¯. С помощью известной формулы определяются координаты векторов K1N¯{-1;2;-3} и KN¯{-1;2;0}. Подставив в формулу для нахождения косинуса угла между векторами соответствующие координаты, получаем cos(KN¯^K1N¯)=√70/14. Поэтому искомый синус sin(KN¯^M1P1PM¯)=√70/14. Задача решена.
Презентация «Метод координат в пространстве. Вычисление углов между прямыми и плоскостями» может применяться для повышения эффективности школьного урока математики. Также данный наглядный материал будет полезен для решения учебных задач учителю, который осуществляет дистанционное обучение. Ученикам, недостаточно хорошо освоившим материал, для формирования стойких навыков решения задач презентация может рекомендоваться в качестве дополнительного материала для самостоятельного рассмотрения.
| Автор | |
|---|---|
| Дата добавления | 07.11.2014 |
| Раздел | Геометрия |
| Подраздел | Презентация |
| Просмотров | 4235 |
| Номер материала | 962 |