
Презентация "Множества, их виды. Способы задания множеств" по дисциплине "Дискретная математика"














Описание презентации по отдельным слайдам:
Основоположник теории множеств «Множество есть многое, мыслимое нами как единое целое» Георг Кантор (1845-1918) немецкий математик, основоположник теории множеств
2. Виды множеств Опр. Два множества, имеющие одинаковую мощность, называются равномощными. Напр.: А – множество цветов радуги В – множество нот .
2. Виды множеств Опр. Два множества называются равными, если они содержат одни и те же элементы. Обозначение: А = В (!!) Если А = В, то |А| = |В| .
3. Способы задания множеств . Этот способ используется только для конечных множеств. Напр.: M = {понедельник, вторник, среда, четверг, пятница, суббота, воскресенье}
3. Способы задания множеств . Порождающая процедура описывает способ получения элементов множества из уже полученных элементов, либо из других объектов. Этот способ используется для бесконечных множеств. Напр.: а) M = {1, 1, 2, 3, 5, 8, 13, 21,…} m1 = 1, m2 = 1, mn+2 = mn + mn+1 – порождающая процедура б) А = {2, 4, 6, 8, 10,…} an = 2n – порождающая процедура
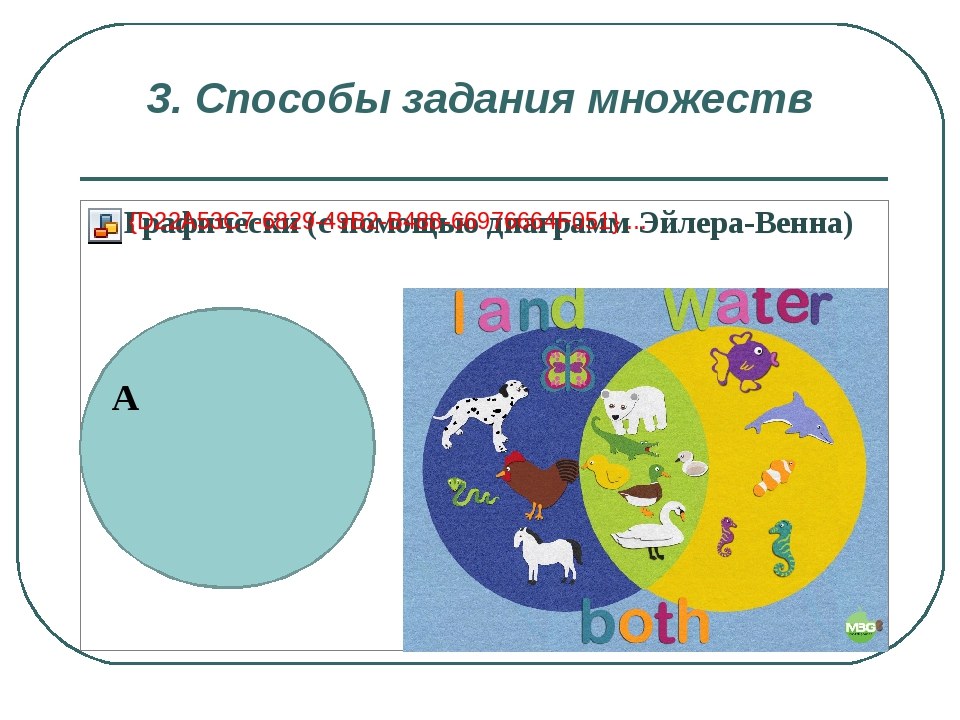
3. Способы задания множеств . Характеристическое свойство – это такое свойство, что элементы множества им обладают, а все остальное на свете не обладает. Этот способ применим как к конечным, так и бесконечным множествам. Напр.: а) Герои романа Л. Н. Толстого «Война и мир» б) М = { x| 0 ≤ x ≤ 1} – множество всех действительных чисел таких, что они заключены между 0 и 1 включительно.
4. Подмножества. Универсальное множество Опр. Множество В называется подмножеством множества А, если всякий элемент множества В является элементом множества А. Обозначение: В ⊂ А Напр.: N ⊂ Z ⊂ Q ⊂ R ⊂ C (!!) 1) Если А ⊂ В и В ⊂ А, то А = В. 2) Если А – некоторое множество, то Ø ⊂ А и А ⊂ А.
4. Подмножества. Универсальное множество Опр. Подмножества А и Ø множества А называются несобственными подмножествами множества А. Любое другое подмножество называется собственным подмножеством этого множества. Напр.: А = {1; 2; 3} {1}, {2}, {3}, {1; 2}, {1; 3}, {2; 3} – собственные подмножества
4. Подмножества. Универсальное множество Опр. Множество всех подмножеств некоторого множества А называется его булеаном. Обозначение: В(А) Напр.: А = {a; b} B(A) = { Ø; {a}; {b}; {a; b}} (!!) |B(A)| = 2|A|, т.е. множество, содержащее п элементов, имеет 2п подмножеств.
4. Подмножества. Универсальное множество Опр. Воображаемое множество, содержащее в себе все другие множества, называется универсальным. Обозначение: U U А

| Автор | |
|---|---|
| Дата добавления | 21.12.2018 |
| Раздел | Высшая математика |
| Подраздел | Презентация |
| Просмотров | 3193 |
| Номер материала | 6001 |