
Презентация "Неравенства с модулем"

Краткое описание документа:
Презентация «Неравенства с модулем» представляет наглядный материал для изучения данной темы на школьном уроке. В ходе презентации представлены способы решения неравенств, содержащих модули выражений. При создании слайдов используется ряд инструментов, помогающих активизировать процессы запоминания материала, удерживать внимание учеников на обучении, легче сформировать умения в решении неравенств с модулем.


Презентация начинается с представления примеров неравенств с модулем. На данном уроке рассматриваются виды неравенств, которые
- содержат в одной части неравенства выражение под знаком модуля;
- содержат выражения под знаком модуля в обеих частях неравенства;
- части неравенства содержат выражения, в которых есть выражения под модулем.
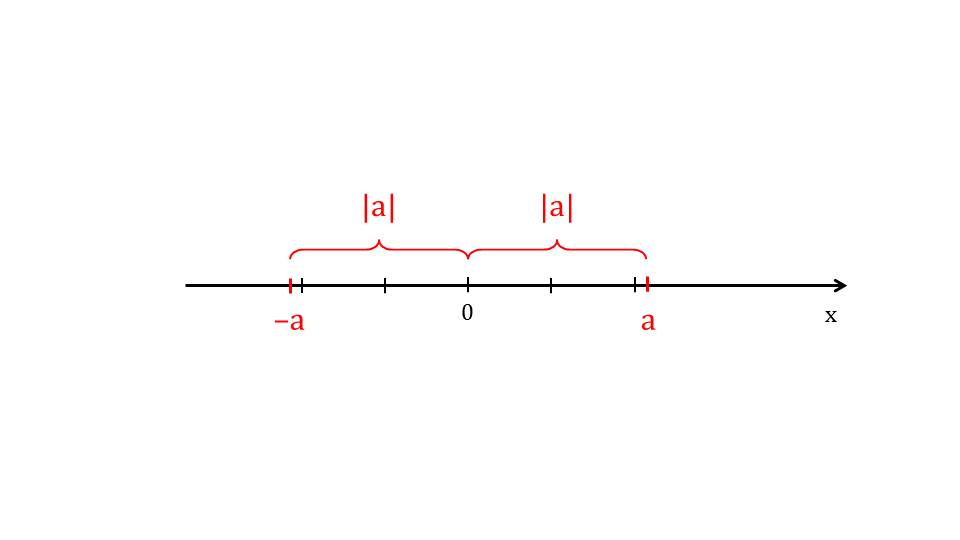
Далее ученикам напоминается понятие модуля. На втором слайде представлено определение модуля, выделенное в рамке. Отмечается, что модулем числа является само число в случае, когда оно неотрицательное, или этому числу с противоположным знаком, если число отрицательное. Смысл операции модуля рассматривается на рисунке – на слайде 3 изображена числовая ось, на которой отмечена точка с координатой а и противоположная ей точка с координатой –а. От начала координат до каждой из точек измеряется расстояние |а|.

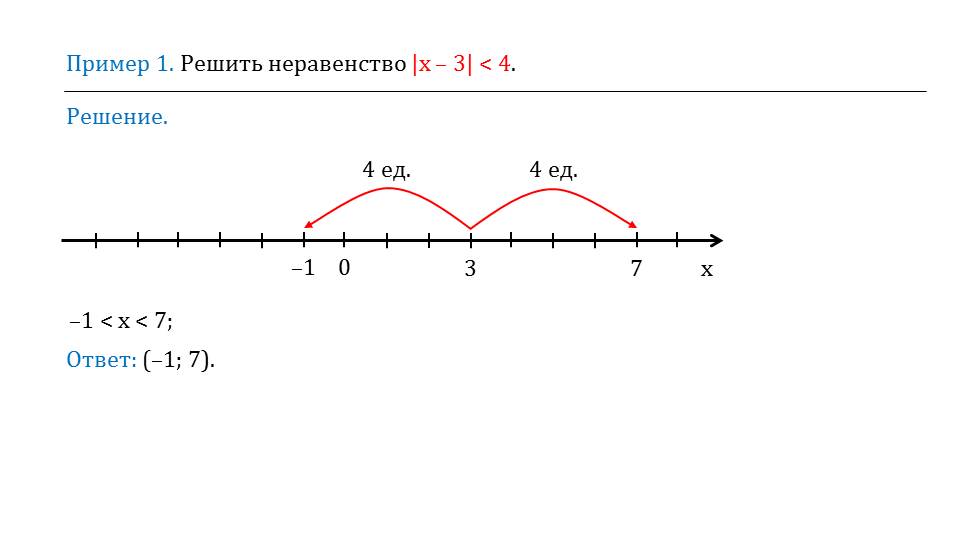
Далее описан геометрический смысл модуля, способ 1 решения неравенств с модулем. Описывается решение неравенства |х-3|<4. Под условием изображается числовая прямая. Отмечается точка х=3, от которой отсчитывается расстояние 4. От данной точки вправо и влево откладывается 4 единицы, и отмечаются точки, соответствующие условию неравенства. Решение неравенства соответствует множеству решений, лежащих на промежутке -1<x<7. Таким образом определяется геометрический смысл модуля как расстояния от выбранной точки до выбранного нуля.

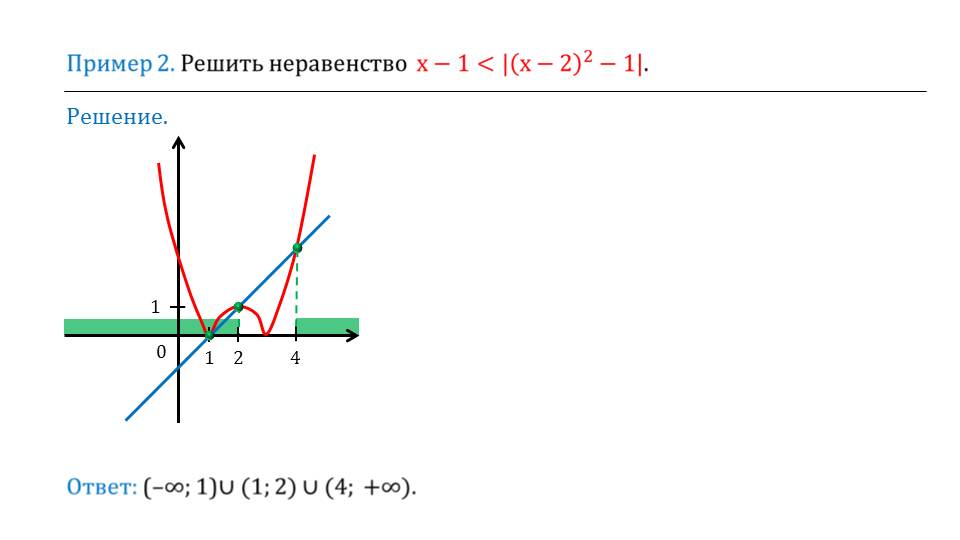
На слайде 6 представляется графический способ решения неравенств, содержащих модуль. В качестве примера выбрано описание решения неравенства х-1<|(x-2)2-1|. На рисунке изображается координатная плоскость, на которой чертятся графики функций, соответствующих левой и правой частям неравенства у=х-1 и у=|(x-2)2-1|. Находим пересечение графиков данных функций – это три точки х=1, х=2, х=4. Определяются промежутки, на которых условие неравенства исполнено. Решением данного неравенства является объединение промежутков (-∞;1)U(1;2)U(4;+∞).

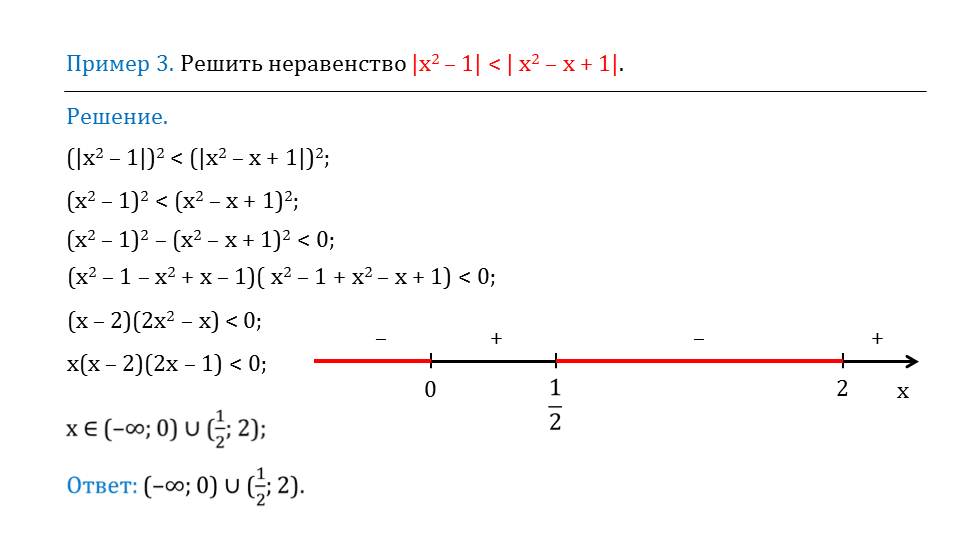
Следующий способ решения неравенств с модулем представлен на слайде 8 – возведение в квадрат. Применение данного способа демонстрируется на примере решения неравенства |x2-1|<|x2-x+1|. Чтобы решить неравенство, обе его части возводятся в квадрат. Затем члены неравенства переносятся в левую часть его так, что в правой части остается нуль. После раскрытия скобок, приведения подобных слагаемых и вывода общего множителя за скобки, получаем неравенство х(х-2)(2х-1)<0. Решение такого неравенства не представляет сложности. На рисунке изображается числовая прямая, на которой отмечены точки х=0, х=1/2, х=2. На каждом промежутке отмечается знак выражения, расположенного в левой части неравенства. Так находим решение – объединение промежутков (-∞;0) и (1/2;2).

Решить неравенство можно также, используя определение модуля. Это четвертый способ, представленный в презентации. В примере 4 описывается решение неравенства 3|x-1|<=x+3. Анализируется значение выражения под знаком модуля. Если x-1 принимает положительное значение, то его модуль равен самому выражению, и после преобразования неравенство принимает вид 2х<=6. В случае, когда x-1 принимает отрицательные значения, модуль выражения равен 1-х, и неравенство после преобразования принимает вид -4х<=0. Решение неравенства получает форму решения двух систем неравенств x-1>=0, 2x<=6 и x-1<0, -4х<=0. Решением первой системы является промежуток [1;3], а решением второй системы является промежуток [0;1]. Так мы нашли решение исходного неравенства – объединение отрезков [0;1]U[1;3].

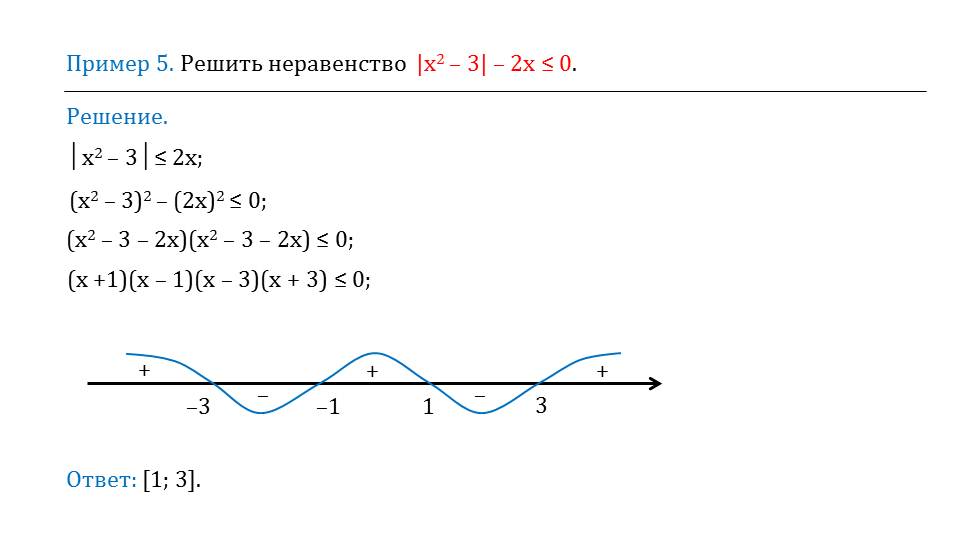
В примерах 5-8 рассматривается решение неравенств различными способами, представленными выше. В примере 5 для решения неравенства |x2-3|-2х<=0 применяется способ возведения в квадрат. После преобразования возведенного в квадрат неравенства, оно принимает вид (х+1)(х-1)(х-3)(х+3)<=0. Имея точки, в которых вероятно изменение знака функции, на числовой прямой отмечаем данные точки и определяем знаки, которые принимает выражение (х+1)(х-1)(х-3)(х+3). В результате анализа получаем решение неравенства [1;3]. В примере 5 также применяется способ возведения обеих частей неравенства в квадрат. После преобразования выражения, возведенного в квадрат, получаем решение неравенства х<-1.
Для решения иррационального неравенства х-1>3√(х3-2х2+4х-7), представленного на слайде 14, также применяется способ возведения в степень.
Так как в правой части выражение под корнем 3-й степени, то обе части неравенства возводятся в степень 3. В результате преобразований возведенных в степень частей неравенства, получаем простое квадратное неравенство х2+х-6<0. Его решением является промежуток (-3;2).
Последний пример описывает решение неравенства (2х+3)2-|2x+3|<=30. Неравенство решается способом введения новой переменной. Для этого выражение |2x+3| принимается за переменную у. Исходное неравенство преобразуется с подстановкой данной переменной в неравенство у2-у-30<=0. Решив данное квадратное неравенство, получаем решение -5<=|2x+3|<=6. Данное неравенство решается системой неравенств |2x+3|<=6 и |2x+3|>=5. В результате вычислений получаем хϵ[-4,5;1,5].



Презентация «Неравенства с модулем» применяется для наглядности учебной информации, представляемой на традиционном уроке. Материал может быть полезен на уроке по данной теме в ходе дистанционного обучения. При необходимости освоить способы решения неравенств с модулем учениками самостоятельно, презентация может быть рекомендована для самостоятельной работы дома.
| Автор | |
|---|---|
| Дата добавления | 16.11.2014 |
| Раздел | Алгебра |
| Подраздел | Презентация |
| Просмотров | 8263 |
| Номер материала | 1046 |