
Презентация "Неравенства с параметрами"

Краткое описание документа:
Презентация «Неравенства с параметрами» является наглядным пособием к одноименному школьному уроку математики. Задача данной презентации – облегчить задачу учителя в формировании навыков учеников в решении неравенств с параметрами. Несмотря на то, что ученики имеют достаточные теоретические знания в решении уравнений и неравенств, а также практические навыки, работа с параметрами может вызвать сложность. Поэтому использование наглядного материала, облегчающего понимание методов решения и особенностей работы с параметрами, целесообразно и желательно. В ходе презентации ученики знакомятся с понятием неравенства с параметрами как отдельным объектом изучения, на примерах рассматривают решение подобных неравенств. Данный тип неравенств имеет важное практическое значение и встречается в математическом моделировании. Поэтому выработка навыков их решения очень важна. С помощью презентации учителю легче удержат внимание учеников на изучении темы. Приемы акцентирования внимания на отдельных понятиях активизируют процессы запоминания теоретического материала и методов решения. Анимационные эффекты и цветное представление хода решения неравенств помогают усвоить изучаемый материал.
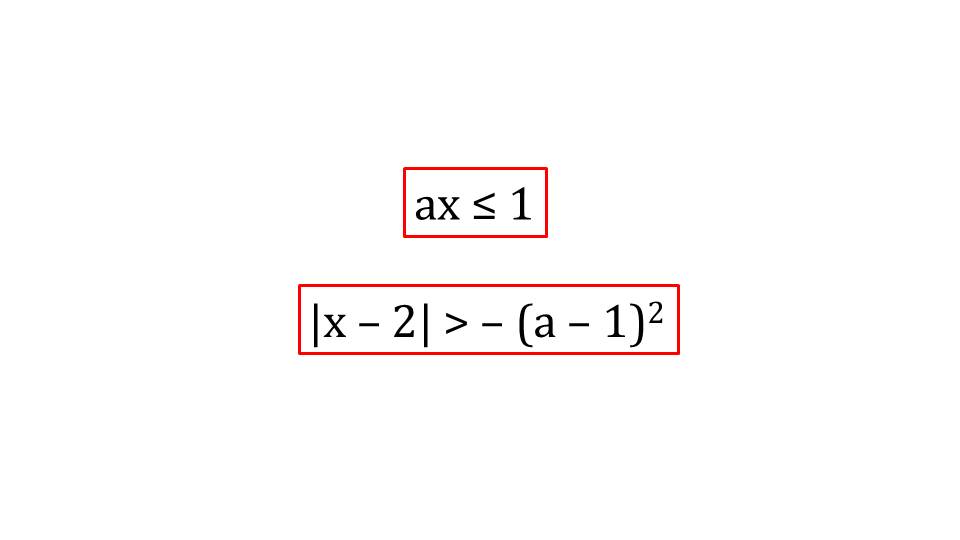

Демонстрация начинается с представления примеров неравенств с параметрами ах<=1 и |x-2|>-(a-1)2. Далее рассматриваются теоретические основы, которыми необходимо оперировать при решении неравенств с параметрами. В тексте слайда 2 раскрывается смысл понятия, что означает решить неравенство с параметром. В рамке выделено, что это значит для каждого значения параметра определить множество решений неравенства или доказать их отсутствие. Далее напоминается вид неравенств первой степени – на слайде 3 отмечается, что неравенствами первой степени, или линейными неравенствами являются неравенства вида ах+b>0, ах+b>=0, ах+b<0, ах+b<=0, в которых a, b – действительные числа, а х - переменная.


На слайде 4 раскрывается алгоритм решения линейного неравенства ах+b>0 с параметром а. Решение разбивается на три части, когда рассматривается а>0, а<0 и а=0. В первом случае, когда а>0, из неравенства определяется х>-b/a. Решение неравенства представляет собой множество (-b/a;+∞). Во втором случае рассматривается отрицательная а. В этом случае из исходного неравенства следует решение х<-b/a. Множество решений лежит на промежутке (-∞;-b/a). В последней части решения оценивается множество значений переменной х при а=0. При подстановке значения а=0 в неравенство получаем 0·х+b>0. Очевидно, при положительном b всякое положительное действительное число является решением неравенства, а при отрицательном b неравенство не имеет решений. Далее рассматриваются решения неравенств с параметром.
В примере 1 необходимо решить неравенство ах<=1. Согласно плану, который прописан в алгоритме, решение состоит из трех частей. В первой части для положительного а находится значение х<=1/a. Во второй части для отрицательного а находим х>=1/a. Подставляя в неравенство а=0, замечаем, что для любого действительного х неравенство будет верно 0·х<=1. Задача решена.


Во втором примере требуется найти множество решений неравенства |x-2|>(a-1)2. Чтобы решить неравенство, сначала отмечаем, что левая его часть всегда неотрицательная, а правая часть неравенства неположительная. При а=1неравенство будет верно при любом действительном значении х, кроме х=2. При а≠1 х принимает любое действительное значение.
На слайде 7 представлено решение третьего примера 3(4а-х)<2ах+3. Перед решением неравенства, оно преобразуется так, чтобы в обеих частях были произведения, при этом правая часть не содержит переменную. Сначала рассматривается случай, когда 2а+3>0, то есть а>-3/2. Из неравенства выражаем х через параметр: х>3(4а-1)/(2а+3). Второй случай – условие 2а+3<0, то есть а<-3/2. Решением в данном случае будет х<3(4а-1)/(2а+3). При а=-3/2 переменная х принимает любое действительное значение – неравенство будет верным.


В примере 4 необходимо решить неравенство √(х-а)+ √(2а-х)+√(а-1)+√(3-а)>0. Очевидно, допустимыми значениями при решении неравенства будут значения параметра, при которых подкоренное выражение принимает положительное значение. Образуются системы неравенств а-1>=1 и 3-а>=0, а также х-а>=0 и 2а-х>=0. Из данных неравенств находим решения – если аϵ[1;3], то хϵ[а;2а].
В последнем примере необходимо определить множество значений а, при которых неравенство √(х2-х-2)+√(2-х)/(х+4)>=ах+2-√(х+1)/(5-х) не имеет решений. Чтобы решить задачу, составляется система неравенств – из а-1>=0, (2-х)/(х+4) >=0, (х+1)/(5-х) >=0, Из нее получается система систем неравенств х=-1, 1>=-а+2, и х=-1, а>=1. Анализируя множество решений, получается аϵ(-∞;1/2]U[1;+∞). Соответственно, не имеет решений данное неравенство на промежутке (-1/2;1). Задача решена.

Презентация «Неравенства с параметрами» применяется на традиционном школьном уроке математики для повышения его эффективности. Данное пособие успешно может использоваться при дистанционном обучении. Так как материал содержит подробное понятное объяснение решения задач подобного типа, материал может быть рекомендован ученикам для самостоятельной работы дома.
| Автор | |
|---|---|
| Дата добавления | 16.11.2014 |
| Раздел | Алгебра |
| Подраздел | Презентация |
| Просмотров | 4916 |
| Номер материала | 1049 |