
Презентация "Объем цилиндра"

Краткое описание документа:
В предыдущих темах учащиеся ознакомились с понятием объема тела и научились вычислять объем прямоугольного параллелепипеда и призмы. С помощью этой презентации разберем тему «Объем цилиндра».


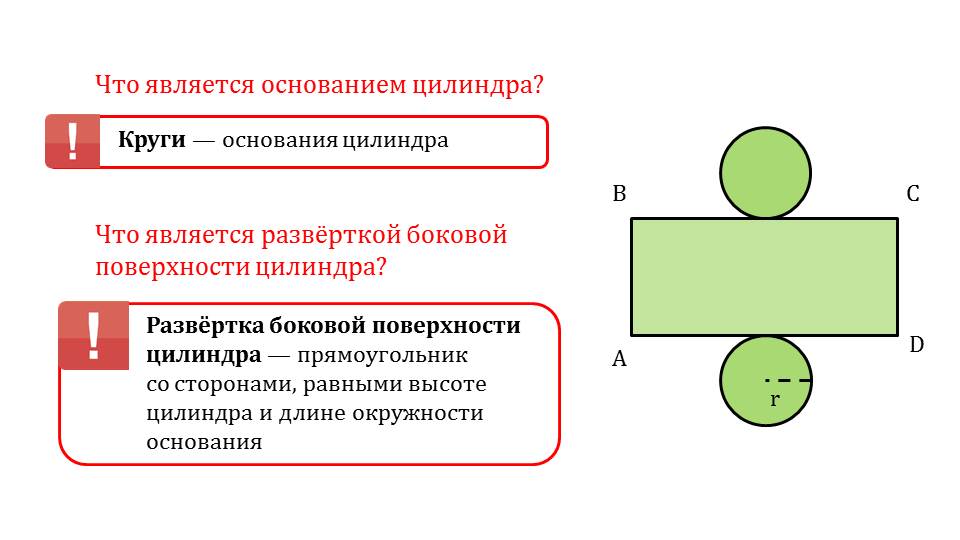
В начале презентации автор предлагает вспомнить основные понятия цилиндра: что такое ось, высота, радиус, основание, развертка боковой поверхности цилиндра. Повторение этих понятий даст возможность изучить новую тему без сложностей. На слайдах автор приводит определения с соответствующими рисунками. Даются также следующие определения:
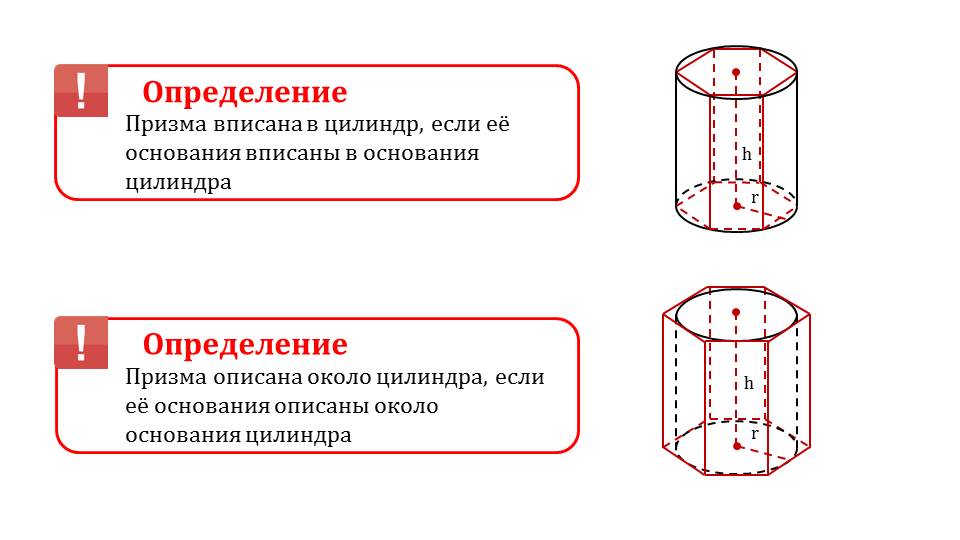
1) если основания призмы вписаны в основания цилиндра, то такая призма является вписанной в цилиндр;
2) если основания призмы описаны около основания цилиндра, то такая призма описана около цилиндра.
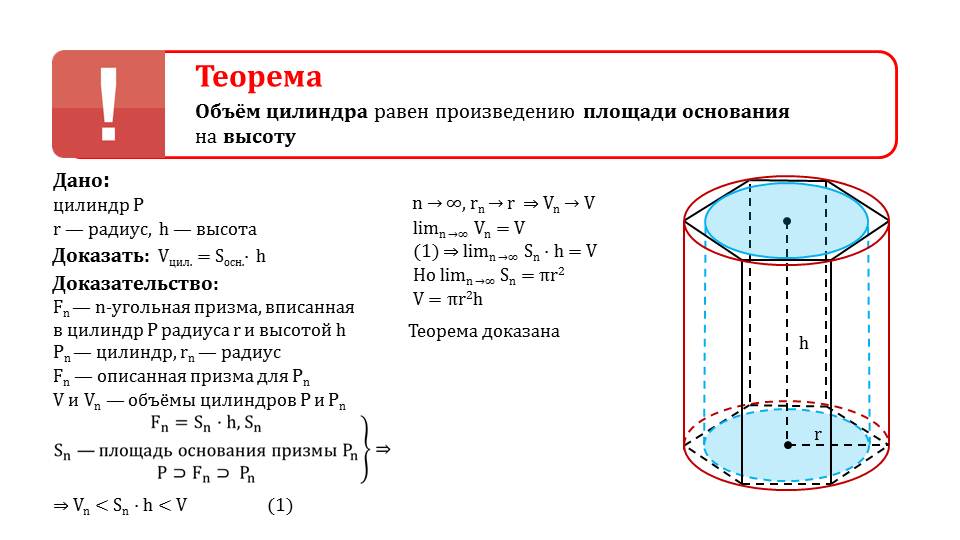
Рассмотрим теорему: объем цилиндра вычисляется как умножение площади основания цилиндра на высоту V = πr2h. Приведем доказательство. Дан цилиндр Р, радиус ивысота. Допустим, что Fn – это призма с количеством n-углов, вписанная в цилиндр Р. Fn будет описанной призмой для цилиндра Pn. Обозначим V и Vn объемы цилиндров. Тогда объем призмы Fn будет равен произведению площади основания призмы на высоту Sn x h. Следовательно, можем записать, что Vn < Sn x h < V. Когда количество углов n призмы будет неограниченно расти, значение объема призмы будет приближаться к значению объемы цилиндра. Тогда, выразив площадь основания призмы через радиус, получим V = πr2h.

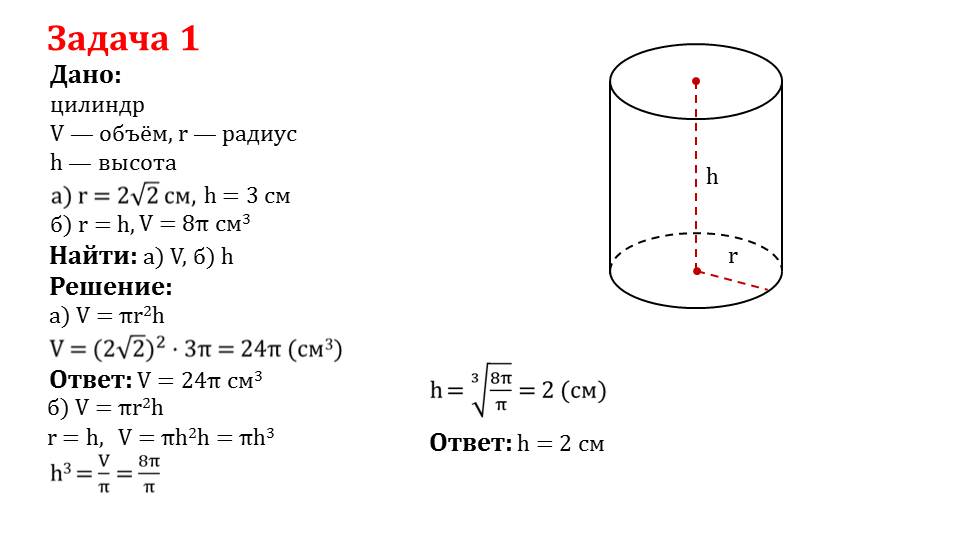
Рассмотрим несколько задач. Задача 1. Дан цилиндр, где V – объем, r – радиус, h – высота.
Вариант а: даются значения радиуса и высоты, нужно найти объем. Подставив значения радиусаи высотыв формулу V = πr2h, найдем объем цилиндра.
Вариант б: дается значение радиуса r = 8π, которое равно значению высоты; необходимо найти высоту. Запишем формулу объема цилиндра V = πr2h = πx h2 x h = π x h3. Решая данное выражение, найдем, что высота h равна 2.
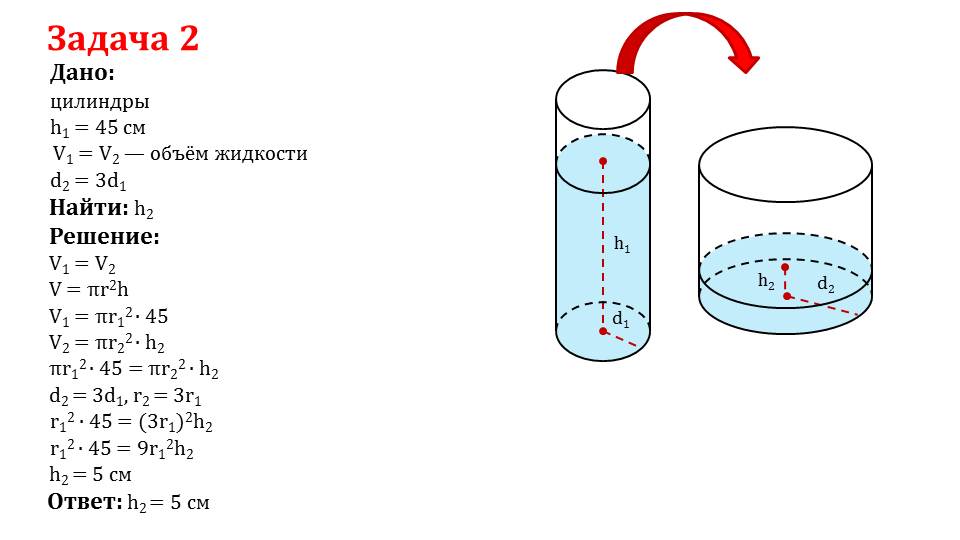
Задача 2. Даны два цилиндра, в которых находится жидкость. Высота жидкости в первом цилиндре равна 45см. Известно, что объемы жидкостей в этих цилиндрах равны V1 = V2, а радиус второго цилиндра в 3 раза больше первого. Необходимо найти высоту жидкости во втором цилиндре. Запишем, объема цилиндра V = πr2h. Для жидкости в первом цилиндре V1 = πx r12 x h1.Для жидкости во втором цилиндре V2 = πx r22 x h2. По условию V1 = V2, тогда πx r12 xh1 = πx r22 xh2 или r12 x h1 = r22 xh2. Зная, что радиус второго цилиндра в 3 раза больше первого d2 = 3d1, получим r12 x 45 = (3r1)2 x h2. Производя вычисления, найдем, что высота второго цилиндра равна 5см.
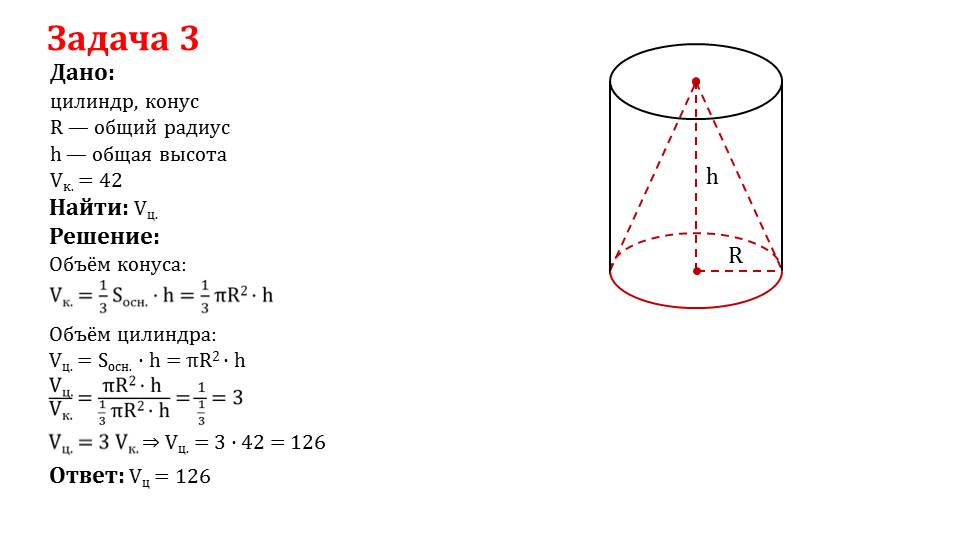
Задача 3. Даны цилиндр и конус, где R – общий радиус, h – общая высота, известен объем конуса VК = 42. Требуется найти объем цилиндра. Сделаем схематический рисунок. Запишем формулу объема конуса VК = 1/3 Sоснx h = 1/3 πR2 x h. Объем цилиндраравен VЦ = Sоснx h = πr2h. VЦ / VК = πr2h / (1/3 πr2h) = 1/ (1/3) = 3. Т.е. VЦ = 3VК, откуда вычислим VЦ = 3 x 42 = 126.
Решение задач по новой теме всегда позволяет лучше закрепить материал и даст возможность перейти к следующей теме.
| Автор | |
|---|---|
| Дата добавления | 07.11.2014 |
| Раздел | Геометрия |
| Подраздел | Презентация |
| Просмотров | 10090 |
| Номер материала | 980 |