
Презентация "Объем наклонной призмы"

Краткое описание документа:
Объемы пространственных фигур относятся к курсу геометрии для учеников старших классов. Презентация «Объем наклонной призмы» позволяет понять само определение фигуры, ознакомиться с теоремой и ее математическим аналогом, а также получить практический опыт на примере использования знаний при решении задач.
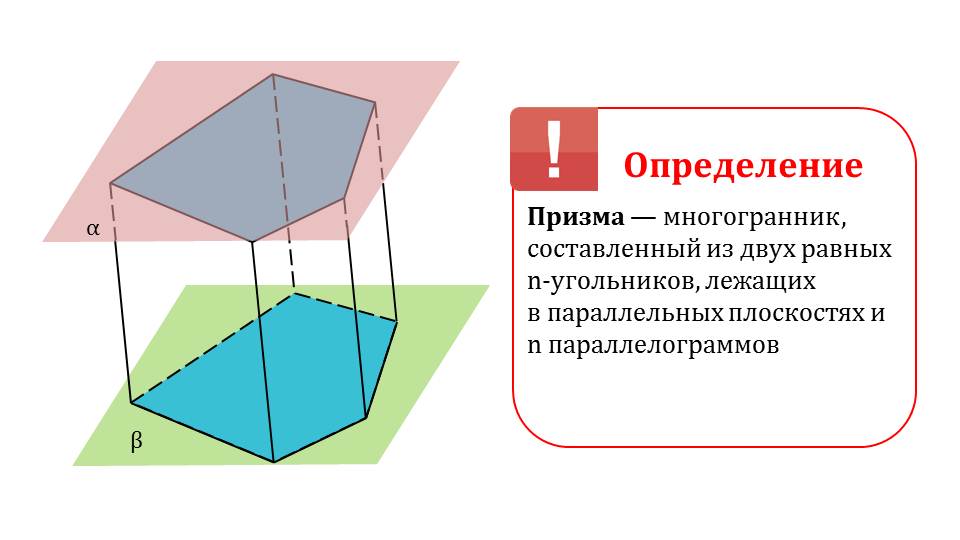
Первая часть презентации ознакамливает учеников с призмой, а также показывает все разнообразие этой пространственной фигуры. На втором рисунке дается определение призмы, которое неразрывно связано с изученным ранее материалом: понятием многоуголников и теоремы о параллельности плоскостей в пространстве. Призма состоит из двух многоугольников, расположенных в параллельных плоскостях и соединенных отрезками, образующими параллелограммы.
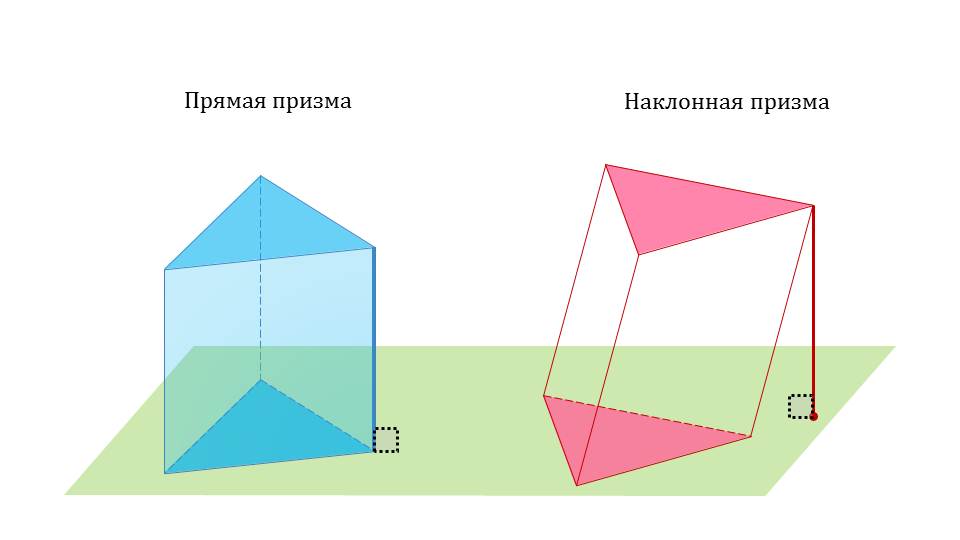
Следующая информация, которую предлагает к изучению презентация, касается разновидностей призм, которые существуют в геометрии. Всего их две: прямая и наклонная призма. Первый вариант фигуры характеризуется параллельностью высоты призмы и ее граней, соединяющих многоугольники. Соответственно каждая из этих граней может считаться высотой призмы. Наклонной призмой считается фигура, где высота и грани расположены между собой под углом. Высотой призмы принято считать отрезок, который расположен под прямым углом к обоим параллельным плоскостям и равен отрезку прямой, расположенному между плоскостями и проходящему через них под прямым углом.
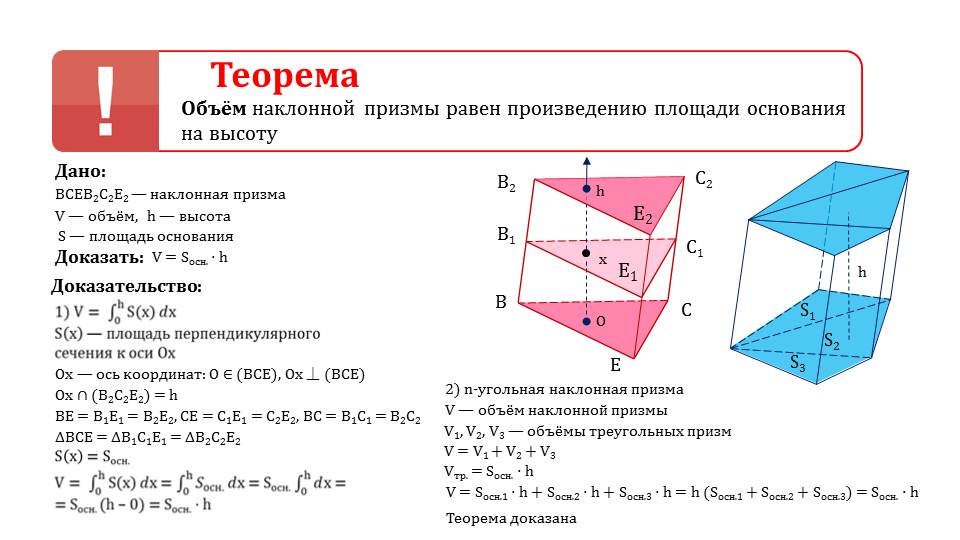
Следующая часть урока заключается в презентации теоремы «Объем наклонной призмы», а также ее математическому написанию.
Предложенная в материале теорема доказывается в двух вариантах: для призмы с треугольными основаниями и для n-угольной фигуры.
Второе доказательство основывается на постулате о возможности деления многоугольника на определенное количество треугольников. Естественно, что объем более сложной призмы равен сумме объемов всех простых призм, на которые была поделена первоначальная фигура.

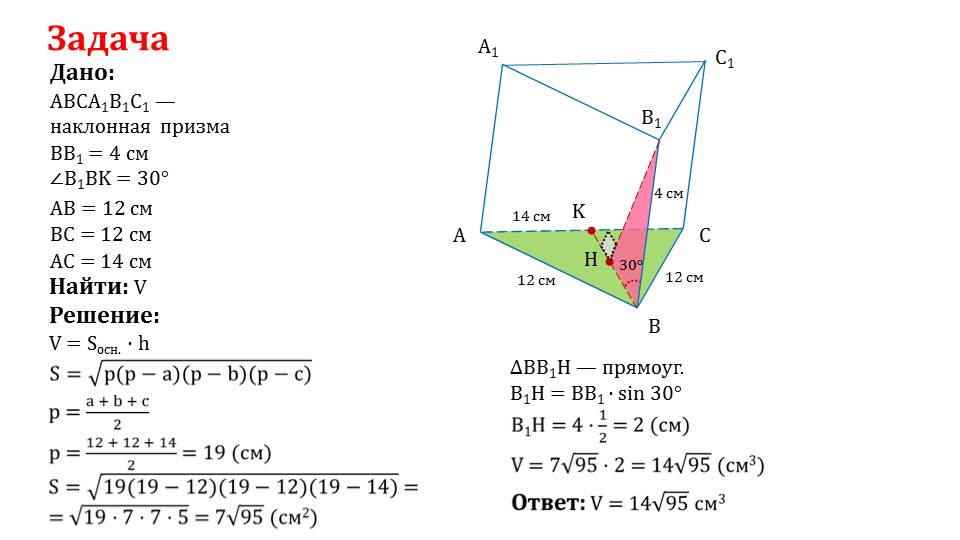
Заключительная часть презентации посвящена решению задачи, где требуется применить знания дополнительных материалов, которые должны быть известны ученикам к этому времени из школьной программы. Для практического применения формулы объема наклонной призмы необходимо знать теорему «площадь треугольника» и уметь работать с тригонометрическими функциями.
Решение задачи разбито на несколько частей. Для нахождение объема наклонной призмы потребуется узнать площадь одного из оснований, а также высоту фигуры, основываясь на данных, записанных в условии задачи.
Понимание последовательных действий в практическом примере, позволит ученикам решать аналогичные задачи, а также использовать формулу для нахождения неизвестного параметра в более сложных типах призм.
Относительная простота презентации, которая подразумевает определенные знания и теоретическую подготовку у обучаемого человека, позволяет эффективно использовать ее в качестве дополнительного пособия при изучении раздела геометрии, связанного с объемом наклонной призмы. Материал можно применять во время проведения занятий, а также в качестве самостоятельной подготовки учеников на дополнительных уроках или в самостоятельной работе.
Удобная структура презентации дает возможность возвращаться к ранее изложенным фактам, так как все картинки и доказательства размещены на одной странице, не требующей времени на загрузку информации. Все важные и необходимые к запоминанию данные оформлены с помощью красной рамки, которая выделяет их на фоне остального материала, позволяя ученику сконцентрировать свое внимание на самом главном.
| Автор | |
|---|---|
| Дата добавления | 07.11.2014 |
| Раздел | Геометрия |
| Подраздел | Презентация |
| Просмотров | 7274 |
| Номер материала | 982 |