
Презентация "Объем прямоугольного параллелепипеда"

Краткое описание документа:
В предыдущей теме учащиеся ознакомились с понятием объема тела и его свойствами. Теперь мы переходим к более детальному изучению объемов конкретных геометрических фигур. В данной презентации рассмотрим, как вычисляется объем прямоугольного параллелепипеда.


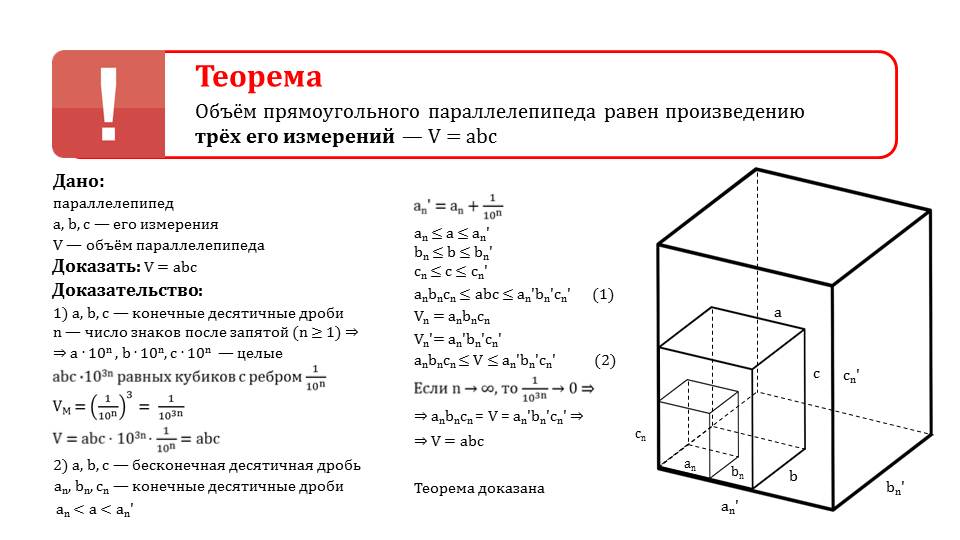
Разберем теорему. Объем прямоугольного параллелепипеда вычисляется умножением его трех сторон между собой V = a x b x c. Разберем доказательство это утверждения. Нам известно, что есть параллелепипед, даны его стороны a, b и с. Рассмотрим несколько случаев.
1) стороны a, b и с – десятичные дроби, которые являются конечными; n – число знаков в дроби после запятой и n ≥ 1. Тогда значения a x 10n, b x 10n, c x 10n будут целыми числами. Если каждое ребро параллелепипеда разделим на части размером 1/10n, и эти части будут равны между собой, и проведем через эти точки сечения, то параллелепипед будет разделен на равные между собой параллелепипеды. Объем такого параллелепипеда (куба) равен abc. Ребро этого параллелепипеда (куба) будет равно значению 1/10n. Тогда объем маленького куба будет равен Vм= 1/103n. Найдем объем исходного параллелепипеда V = a x b x c x 103n x 1/103n = a x b x c.
2) измерения a, b и с – десятичные дроби, которые являются бесконечными. Допустим, что десятичные дробиan, bn и сn конечны, которые получились из значений a, b и с, если удалить цифру после запятой в каждом последующем числе. Запишем, что an' = an + 1/10n, an ≤ a ≤ an'. Аналогично bn ≤ b ≤ bn', cn ≤ c ≤ cn'. Перемножив эти выражения, получим anbn сn ≤ abc ≤ an' bn' cn'.
anbn сn – это Vn, an' bn' cn' – Vn'. Когда значение n будет неограниченно расти, значение 1/10n будет стремится к нулю, следовательно, значения anbn сn и an' bn' cn' будут практически не отличаться друг от друга. Значит, V будет практически не отличаться от значения abc, следовательно, V = abc.
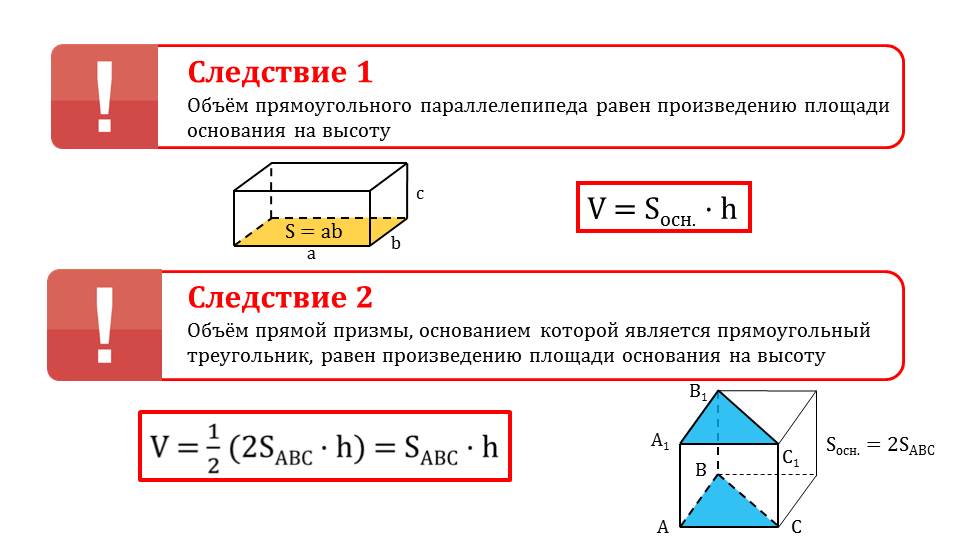
На следующем слайде проиллюстрированы 2 следствия из теоремы.
Следствие 1. Объем прямоугольного параллелепипеда вычисляется умножением площади его основания на высоту V = Sоснx h.
Следствие 2. Если в основании прямой призмы лежит прямоугольный треугольник, то объем этой призмы вычисляется умножением площади основания на ее высоту V = 0,5 (2SABC x h) = SABC x h.
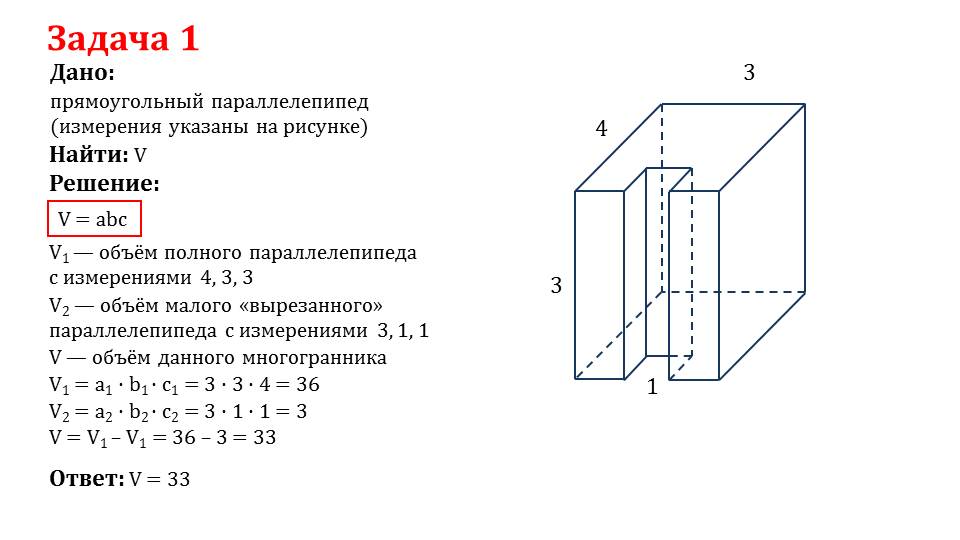
Рассмотрим примеры. Задача 1. Дан прямоугольный параллелепипед, известные стороны отмечены на рисунке. Нужно найти объем нарисованной фигуры. Отметим, что V1 это объем полного параллелепипеда без вырезанной части; V2 – объем вырезанного параллелепипеда; V – объем заданной фигуры. Тогда, зная стороны и вычисляя V1 и V2, найдем V = V2 – V1.
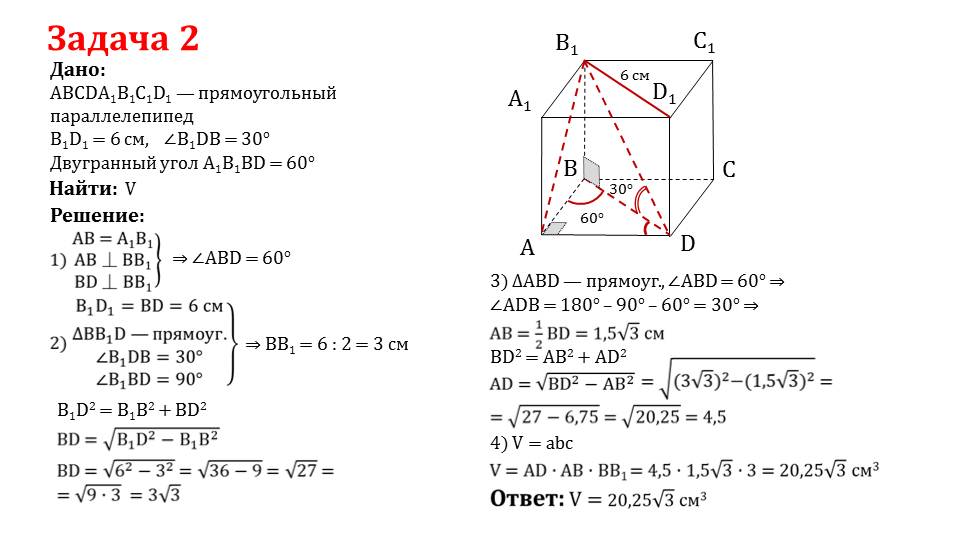
Задача 2. Дан прямоугольный параллелепипед ABCDA1B1C1D1, B1D1 = 6см, угол B1DB равен 30 градусов, двугранный угол A1B1BD равен 60 градусов.
Необходимо найти объем параллелепипеда. Т.к. AB = A1B1, AB перпендикулярна BB1, а BD перпендикулярна BB1, угол ABD равен 60 градусов. Угол B1DB равен 30 градусов, угол B1BD равен 90 градусов, значит треугольник BB1D прямоугольный. B1D1 = BD = 6см, следовательно, BB1 = 6/2 = 3см. Используя теорему Пифагора, найдем в треугольнике BB1D сторону BD. Далее рассмотрим треугольник ABD. Он прямоугольный, угол ABD равен 60 градусов, угол ADB равен 30 градусов. AB = 0,5BD. AD найдем, зная размеры BD и AB. Когда мы вычислили все необходимые размеры, можем найти объем прямоугольного параллелепипеда V = AD x AB x BB1.
| Автор | |
|---|---|
| Дата добавления | 07.11.2014 |
| Раздел | Геометрия |
| Подраздел | Презентация |
| Просмотров | 6135 |
| Номер материала | 978 |