
Презентация "Область определения и область значений функции"

Краткое описание документа:
Данный обучающий материал посвящен изучению области определения и значения функций. Вероятнее всего, десятиклассники в предыдущих классах уже сталкивались с данными понятиями. Однако в этом классе они должны ознакомиться с ними более подробно, изучить более детально.


Любая функция имеет некоторую область определения. Область определения – это некоторый интервал, который включает в себя все x-ы, удовлетворяющие функции, то есть некоторому правилу. Любая функция f(х) задается исключительно вместе с ее областью определения. Стоит отметить, что независимой переменной считается x, то есть аргумент. А значением – y – абсцисса. Значение абсциссы в некоторой точке х обозначается довольно часто как f(x) и читается «эф от икс».


На третьем слайде дается определение понятия область определения. Также дается его обозначение. Далее рассматривается область значений. Как и в предыдущем случае приводятся определение и обозначение данного понятия.
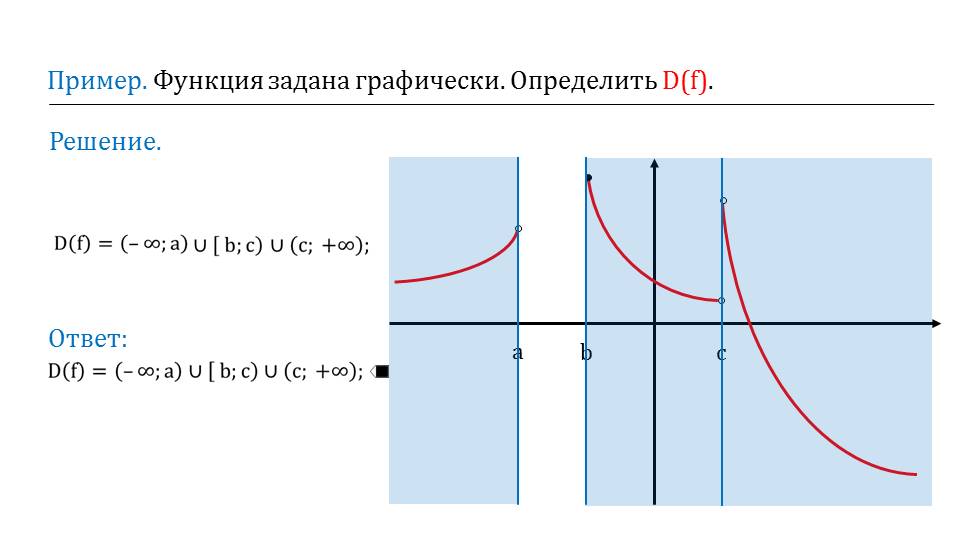
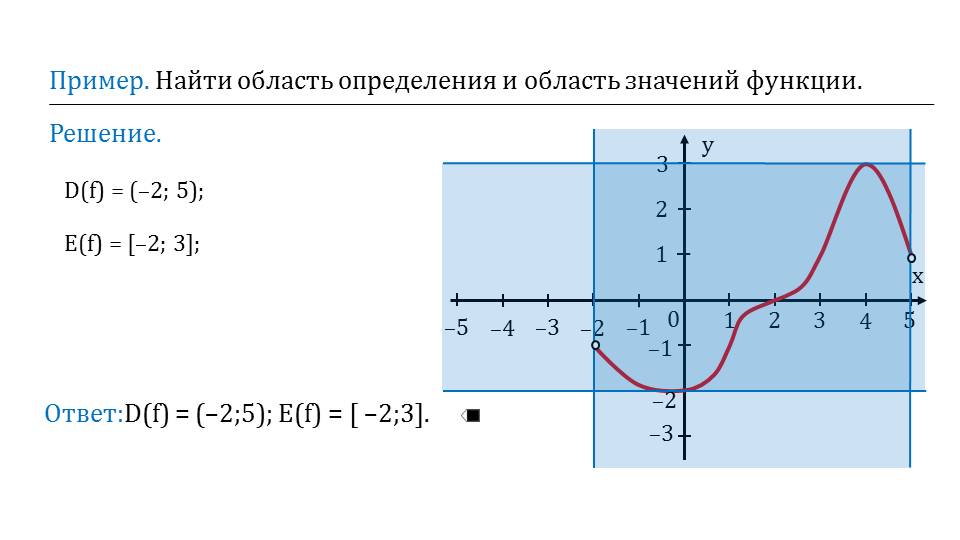
Сразу после того, как даны все определения, приводится первый пример. Можно увидеть некоторую функцию, заданной графическим способом. Предлагается найти область определения данной функции, то есть d(f). Решение приводится графически и выдается ответ.

Шестой слайд посвящен изучению области определения рациональных функций. Они рассматриваются отдельно, ведь имеют некоторую важную особенность, которая влияет на область определений. Если в знаменателе входит аргумент, то из области определения необходимо исключить те значения х-ов, которые превращают знаменатель в ноль, что невозможно.
На следующем слайде приводится алгебраическая запись данного правила. Можно увидеть функцию, в правой части которой имеется дробь, а в знаменателе содержится аргумент. Демонстрируется задание, в котором необходимо найти область определения рациональной функции.
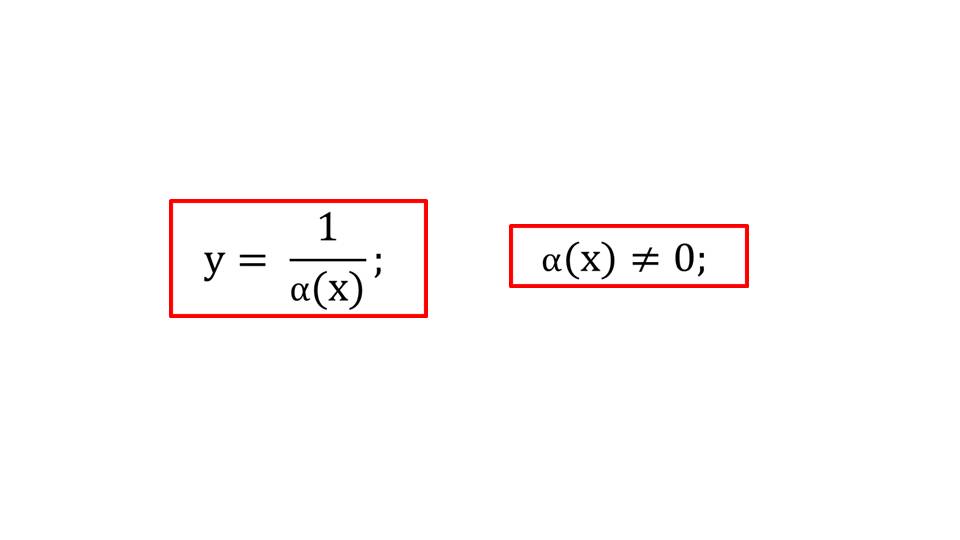

Приводится подробное решение и ответ. Как видим, изначально знаменатель приравнивается нулю для того, чтобы найти значения аргументов, которые стоит исключить из области определения. Изначально считается, что область определения составляет всю числовую ось, из которой исключаются те или иные значения, которые не удовлетворяю правилу.

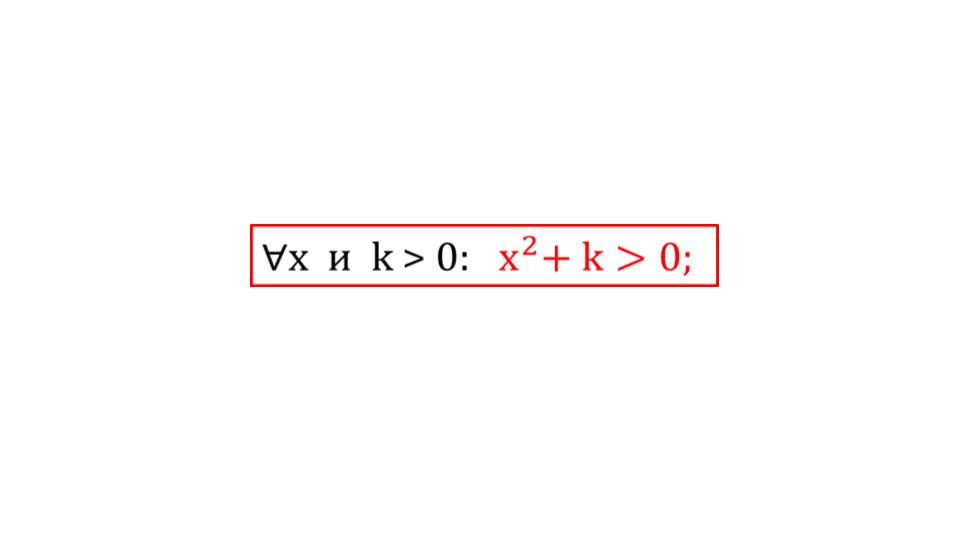
Для того чтобы продемонстрировать школьникам, что область определения может являться и вся числовая ось, приводится пример рациональной функции, в которой любой аргумент имеет смысл. В знаменателе дроби можно увидеть, что, что бы мы не подставили вместо x-а, знаменатель не приравняется нулю. Таким образом, областью определения данной функции являются все действительные числа.


Данный знаменатель на следующем слайде в обобщенном виде. Видим, что аргумент возведен в квадрат и к нему прибавляется некоторое положительное значение k. Что бы мы не подставили вместо x-а, выражение будет положительным. И, даже, при подстановке отрицательного числа при возведении в квадрат знак минуса исчезнет.
После того, как область определения рациональной функции изучена, в презентации предлагается рассмотреть область определения иррациональных функций. Нужно понимать, что подкоренное выражение не может являться отрицательным числом или выражением.


Следующие примеры представляют собой алгебраические записи общих видов иррациональных функций, то есть функций, в которых аргументы входят в подкоренное выражение. Во втором примере, иррациональное выражение стоит в знаменателе. При решении стоит вспомнить, что знаменатель в отдельности нужно рассмотреть. Разумеется, не обойтись без примеров. Первый пример приводит обычную иррациональную функцию. Первым делом проверяется на отрицательность подкоренное выражение.

В некоторых функциях встречаются натуральные логарифмы. Для того чтобы найти область определения таких функций необходимо вспомнить основное свойство логарифма: показатель логарифма является положительным числом. Приводится алгебраическая запись двух случаев. В первом – логарифм встречается в чистом виде, во втором он заключается в знаменателе дроби.
Рассматривается пример, который соответствует второму случаю. Помимо того, что нужно вспомнить и проверить, что показатель натурального логарифма больше нуля, необходимо исключить из области определения те значения х-ов, которые приведут знаменатель к равенству нулю.
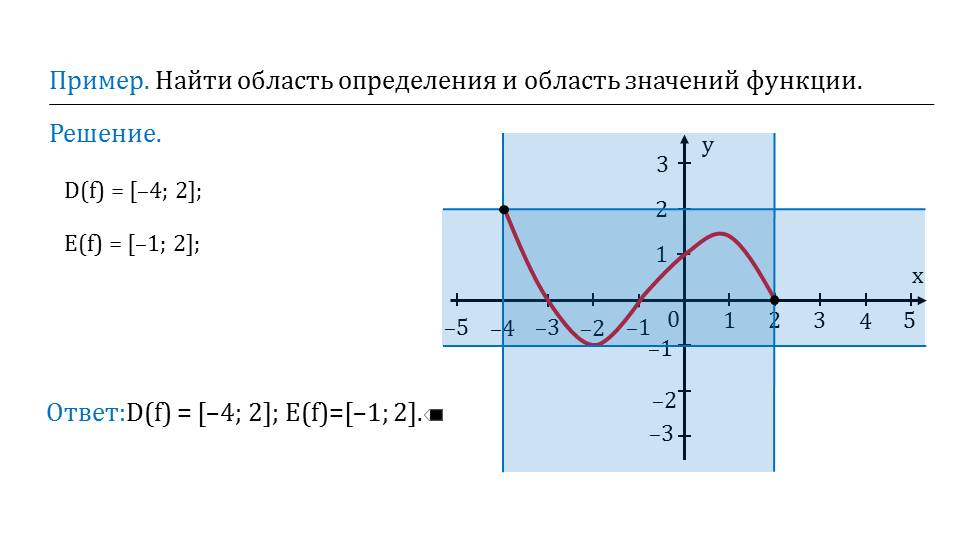
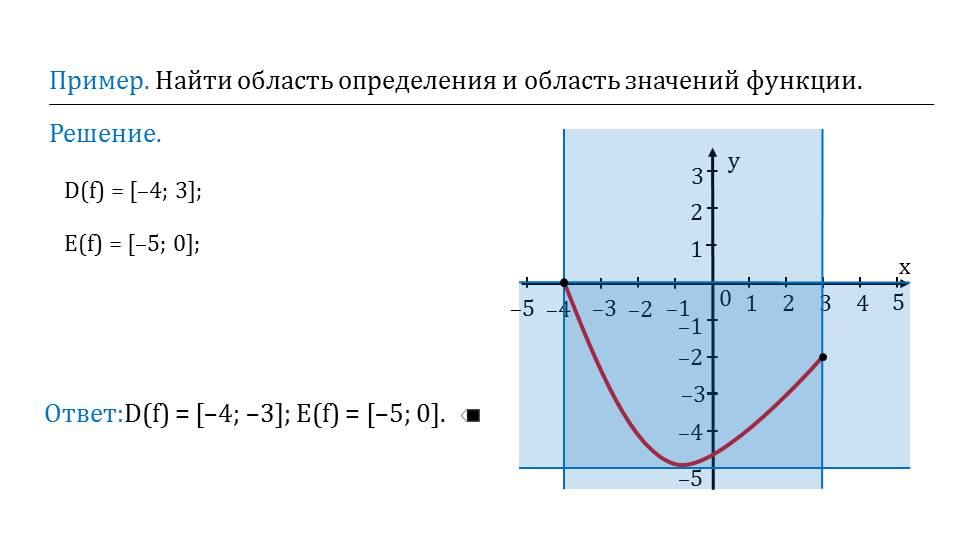
сть определения и область значений графически и записать ответ алгебраически с помощью интервалов. Последующие слайды построены аналогичным образом.
| Автор | |
|---|---|
| Дата добавления | 27.07.2014 |
| Раздел | Алгебра |
| Подраздел | Презентация |
| Просмотров | 6020 |
| Номер материала | 777 |