
Презентация «Определение арифметической прогрессии. Формула n-го члена арифметической прогрессии»

Краткое описание документа:
Данная презентация предназначена для урока алгебры в 9 классе, когда изучаются последовательности, а именно, арифметическая прогрессия.
Автор презентации предлагает для начала рассмотреть конкретную последовательность чисел, которая оказывается арифметической прогрессией. И тут же знакомит обучающихся с ее определением.


Далее поясняется, что некоторая последовательность называется арифметической прогрессией, если выполняется определенное условие, заданное формулой. То есть, чтобы получить следующий член прогрессии, нужно к предыдущему ее члену прибавить определенное число. И это число определяется на следующем слайде, как разность арифметической прогрессии. Здесь же происходит знакомство с формулой нахождения этой разности.


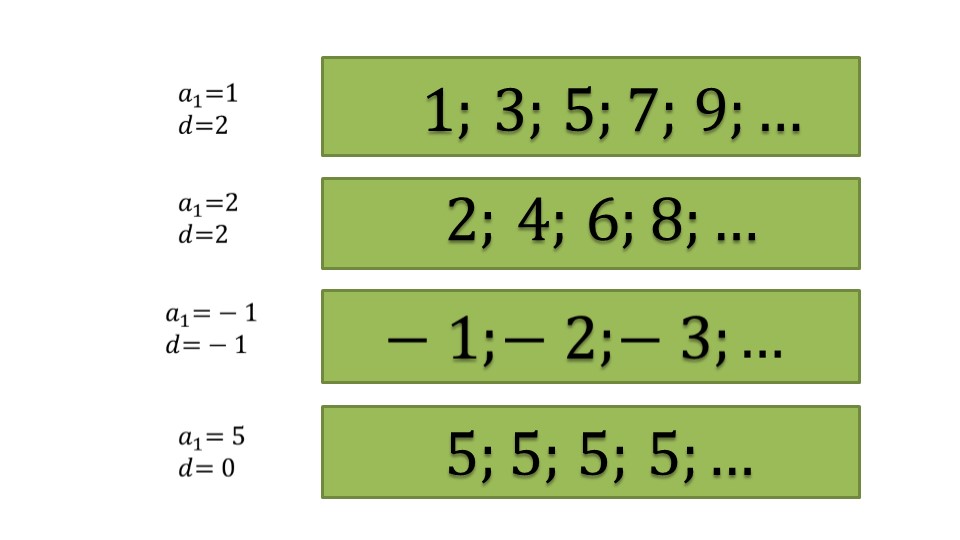
На следующем слайде представлены примеры арифметических прогрессий. Для каждой из них указан 1-ый член и разность.
Далее автор в презентации выводит формулу n-го члена арифметической прогрессии. Для этого находятся несколько первых членов последовательности согласно определению. А затем все члены выражаются через первый член и разность. Так получается общая формула n-го члена. На слайде эта формула выделена в рамку и подписана.

Затем предлагается рассмотреть пример, где дана арифметическая прогрессия. Необходимо найти 40-й член прогрессии, если известен 1-й член и разность. Для этого достаточно воспользоваться только что выведенной формулой, что, собственно, автор презентации и сделал на слайде.
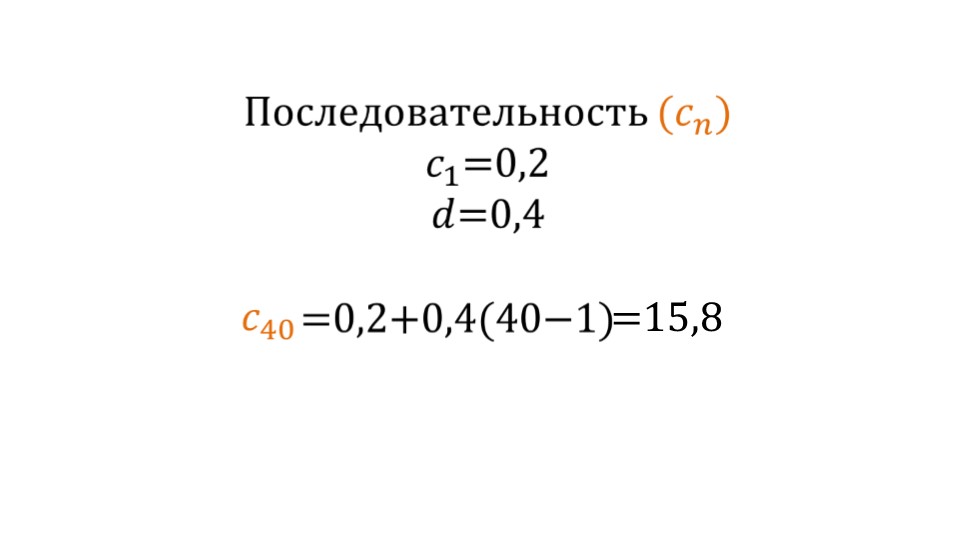

На следующем слайде продемонстрирован пример, где необходимо определить, является ли заданное число членом арифметической прогрессии. Для решения данного примера автор использовал формулу n-го члена арифметической прогрессии. Подставив в формулу 1-й и n-й члены, он стал искать разность арифметической прогрессии. В качестве n-го члена было взято заданное число. В результате оказалось, что полученная разность не является натуральным числом. Отсюда вывод: заданное число не является членом заданной прогрессии.


Далее автор предлагает познакомить обучающихся со свойством арифметической прогрессии, где говорится о том, что любой член такой прогрессии, начиная со 2-го, равен среднему арифметическому предыдущего и следующего членов. К этому свойству прилагается математическая интерпретация: на слайде показан вывод данного свойства.
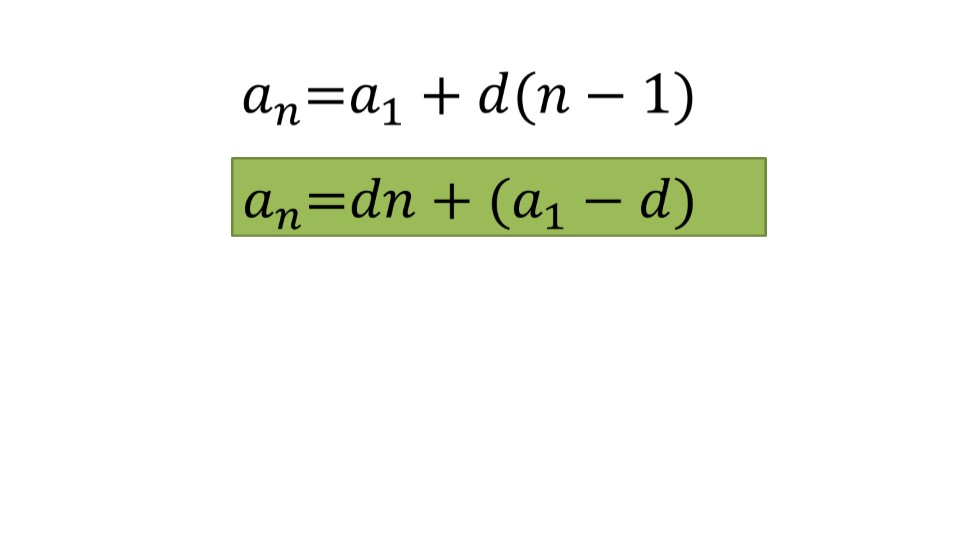

На следующем слайде продемонстрирован признак арифметической прогрессии, который является обратным утверждением свойству арифметической прогрессии. Здесь же производится математическое доказательство этого признака.

Затем на сладе появляется формула n-го члена арифметической прогрессии, которая после небольшого преобразования получает немного иной вид.
На следующем слайде размещено другое свойство арифметической прогрессии, которое связано с той, новой, формулой n-го члена, полученной на предыдущем слайде. И к этому свойству приводится признак арифметической прогрессии. Последний слайд содержит доказательство этого признака.
| Автор | |
|---|---|
| Дата добавления | 29.08.2014 |
| Раздел | Алгебра |
| Подраздел | Презентация |
| Просмотров | 3415 |
| Номер материала | 637 |