
Презентация "Определение и задание обратной числовой функции"

Краткое описание документа:
Данная презентация поможет 10-классникам понять, что такое обратная функция. Материал содержит понятный текст и удобные обозначения. Интерфейс презентации является читабельным. Материал содержит много наглядных примеров и иллюстраций, которые сделают урок более интересным.

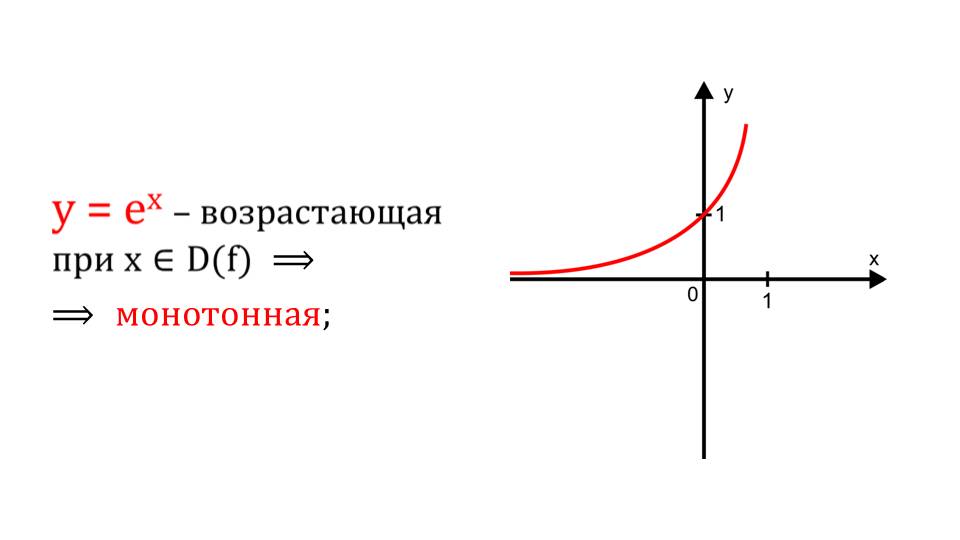
Начинается презентация с того, что напоминается школьникам понятие монотонности. Как уже известно, функция является монотонной, если она либо убывает, либо возрастает на области определения.
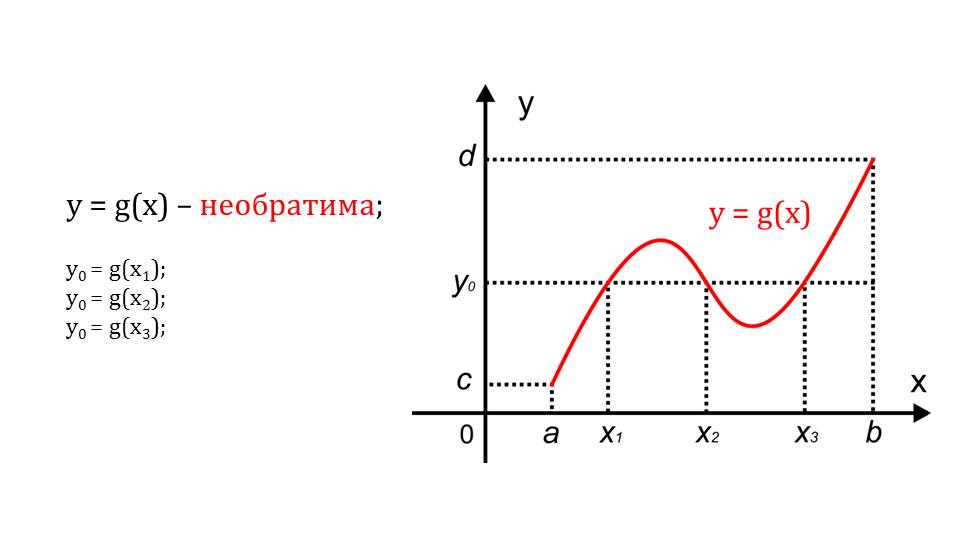
Рассматривается показательная функция, где в качестве показателя степени является х. На графике явно видно, что функция является возрастающей. Если вспомнить определение, то, следовательно, функция является монотонной. Если некоторая функция может принять любое значение исключительно в какой-то точке из области определения, то такую функцию принято называть обратимой.

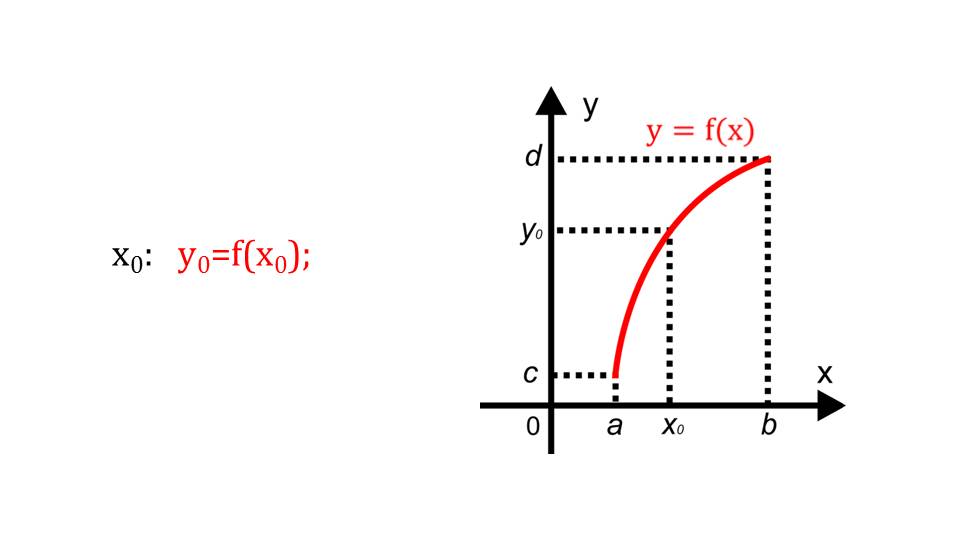
На следующем слайде после данного определения можно увидеть пример, сопровождающийся графиком.
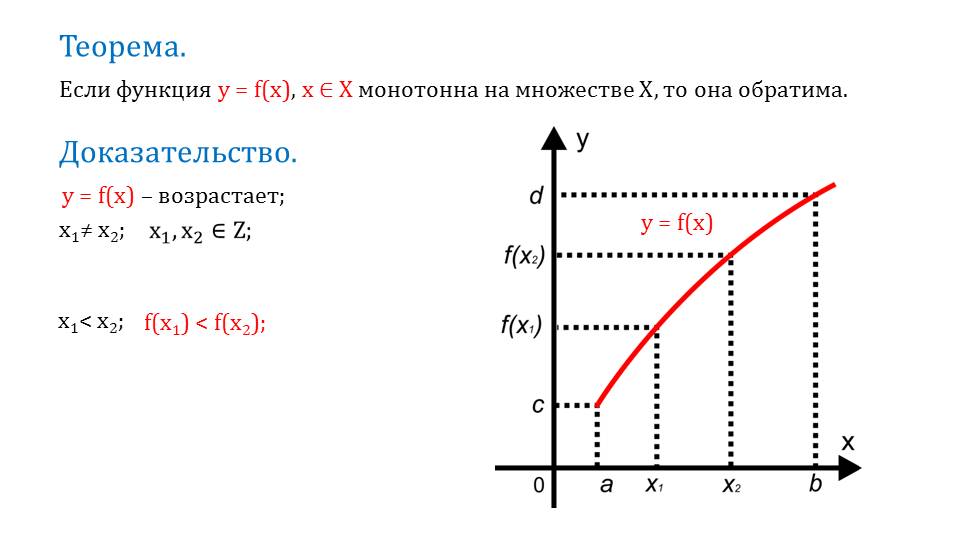
Далее рассматривается теорема. Она гласит о том, что любая монотонная функция на некотором множестве допустимых значений, является обратимой. Приводится также доказательство данной теоремы. Известно, что функция возрастает. Это говорит о том, что два значения аргумента не могут быть равны. Следовательно, одна из значений х-ов будет меньше другой. А, так как функция является возрастающей, то значение ее в данных точках будут, соответственно, больше или меньше друг друга.
Если имеется некоторая обратимая функция с областью определения Х, и областью значения У, то для того, чтобы найти обратную функцию, необходимо возвести ее в -1 степень. Важным моментом является то, что у полученной обратной функции областью определения будет являться У, а область значений, наоборот – Х.


Прямая и обратная функция имеют ряд свойств, которые рассмотрены на следующем слайде. Приводятся некоторые дополнительные рассуждения, для наилучшего понимания.
После этого приводится пример, в котором предлагается рассмотреть некоторую линейную функцию и найти обратную ей. Прежде, чем перейти к решению, необходимо доказать, что такая функция существует. Решение приводится пошаговым образом.


Второй пример посвящен нахождению обратной функции для функции, графиком которой является парабола. Однако предлагается рассмотреть функцию не на всем промежутке, а только лишь на положительном интервале и точки 0. Обратной функцией от параболы представляет собой иррациональная функция корень из х.
И, наконец, третий пример предлагает найти обратную функцию к степенному выражению «х в кубе». Ответ также является иррациональной функцией.


Далее приводится замечание, говорящее о том, что свойство монотонности функции является исключительно достаточным условием, но, ни в коем случае, не является необходимым.
Чтобы у школьников остался алгоритм для нахождения обратной функции у любой другой монотонной функции, на последнем сайте приводится пошаговая инструкция для этого.


Презентация является наглядным и полезным примером для использования в процессе образования. Она поможет провести интересный урок для 10-классников. Также подойдет отлично в качестве материала для самостоятельного изучения.
| Автор | |
|---|---|
| Дата добавления | 27.07.2014 |
| Раздел | Алгебра |
| Подраздел | Презентация |
| Просмотров | 3370 |
| Номер материала | 781 |