
Презентация "Определение производной"

Краткое описание документа:
Презентация «Определение производной» демонстрирует наглядный материал, помогающий освоить данную тему. В ходе презентации представляется материал, раскрывающий физический и геометрический смысл производной функции в некоторой точке, приводятся примеры решения задач, использующих изученный материал.

Презентация помогает повысить эффективность урока математики, формирует представление учеников о предмете изучения, умение находить производную функции в заданной точке.

Использование презентации разнообразит ведение урока, удерживая внимание учеников на обучении. Кроме того, эта форма наглядности имеет много преимуществ, способствующих повышению эффективности урока.


Применение анимации улучшает представление материала, дает возможность подавать его последовательно, наглядно отображая процессы изменений и преобразований. Также в презентации можно использовать рисунки, выделение цветом формул, деталей построения, определений.


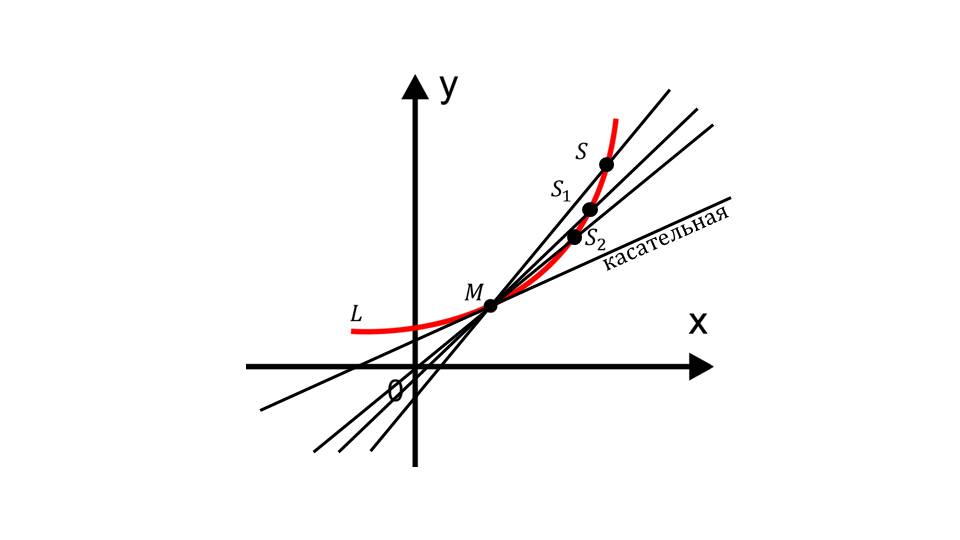
Презентация начинается с описания закона движения, изучаемого в курсе физики. Представлена формула, отображающая изменение перемещения в зависимости от времени S=S(t). Объяснение иллюстрировано с помощью рисунка, на котором изображена числовая ось с началом координат, отрезком LK, характеризующим изменение положения тела ΔS. Очевидно, перемещение тела в некоторый момент времени определяется длиной отрезка OL= S(t). Через некоторое время t+Δt значение перемещения равно промежутку ОК= S(t+Δt).


Приращение функции будет равно изменению дины отрезка LK=OK-OL= S(t+Δt)- S(t), то есть LK= ΔS. На отрезке времени [t, t+Δt] средняя скорость определяется vср= ΔS/ Δt. Скорость в некоторый момент времени может быть выражена формулой vt=limvср при Δt→0. Соответственно, v=limΔS/ Δt при Δt→0. На слайде 2 демонстрируется график перемещения тела, скорость которого определяется построением касательной в данной точке М.

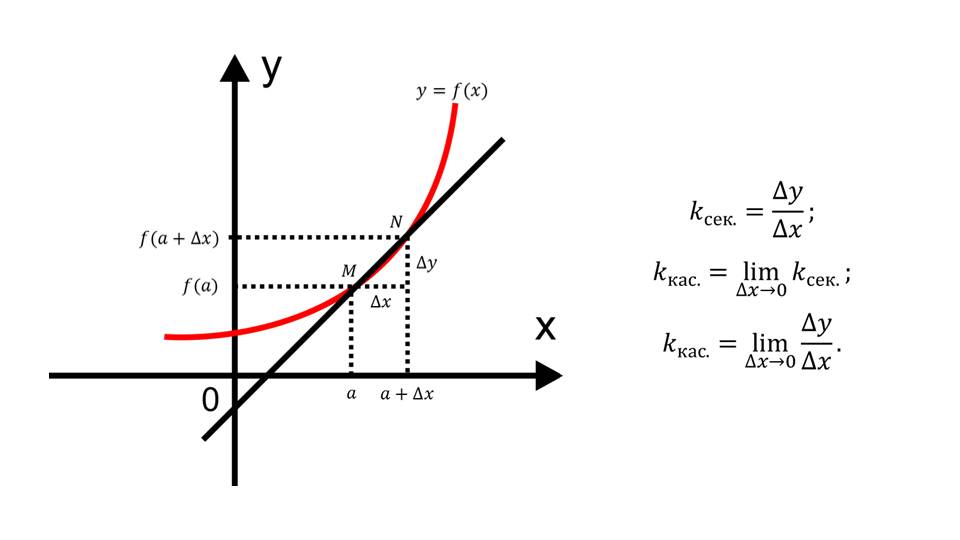
На слайде 3 демонстрируется построение графика некоторой функции у=f(х) и прямой, проходящей через точки MN, принадлежащие графику функции. При изменении переменной а на Δа отмечается изменение значения функции с f(а) до f(а+Δх). При этом если уменьшать изменение аргумента Δх→0 отношение Δу/ Δх будет стремиться к касательной к данному графику в точке, то есть k=limΔу/ Δх при Δх→0.
Рассмотрев практическое значение понятия производной, дается ее определение. Для функции, определенной в некоторой точке и окрестности рассматривается приращение аргумента, не выходящее из окрестности. Если существует предел отношения Δу/ Δх при Δх→0, то данный предел является производной функции в этой точке. Вводится обозначение производной limΔу/ Δх=f΄(x) при Δх→0.


На слайде 5 описываются примеры нахождения производной. Например, для y=kx+m производная равна limΔу/ Δх=kпри Δх→0. Иначе полученный результат можно написать y΄=(kx+m)΄=k. Аналогично находится предел функции у=х3. Так как значение предела limΔу/ Δх= 3х2, то и производная у΄=(х3)΄= 3х2.


Описанные в начале презентации примеры даеют представление о физическом и геометрическом смысле производной. На слайде 6 отмечается, что физический смысл производной – выражение мгновенной скорости тела в некоторый момент времени v=S΄(t). Геометрический смысл производной – указание углового коэффициента касательной, проведенной в точке х=а к графику функции у=f(х).


На слайде 7 дана еще одна важная запись, характеризующая приращение значения функции. Для функции, в токе х которой существует предел limΔу/ Δх= f΄(x) при Δх→0, отношение ее приращения значения к приращению аргумента Δу/ Δх≈f΄(x). Иначе можно записать Δу≈f΄(x)·Δх. Например, для функции у=х3 приращение Δу≈3х2·Δх.


Определение производной функции в некоторой точке на слайде 8 выведено в виде алгоритма действий. В нем предусмотрено нахождение f(х) в фиксированной точке х, определение приращения аргумента (х+Δх) и вычисление значения функции f(x+Δх). Затем определяется приращение функции Δу= f(x+Δх)- f(x), составляется отношение Δу/ Δх и вычисляется его предел limΔу/ Δх= f΄(x) при Δх→0.

Закрепление материала выполняется на основе описания примера. В примере 1 нужно найти производную постоянной у=С. Действуя согласно алгоритму нахождения производной, описывается поиск предела limΔу/ Δх= lim 0=0 при Δх→0.
В примере 2 необходимо найти производную функции у=1/х. Решение выполняется согласно алгоритму. В результате вычислений получаем limΔу/ Δх= lim (-1/х(х+ Δх ))=- 1/х2 при Δх→0. Поэтому (1/х)΄=- 1/х2.


Далее дается понятие функции, дифференцируемой в точке х как функции, имеющей в данной точке производную. Нахождение производной функции при этом называют дифференцированием. Определение выделено для запоминания.
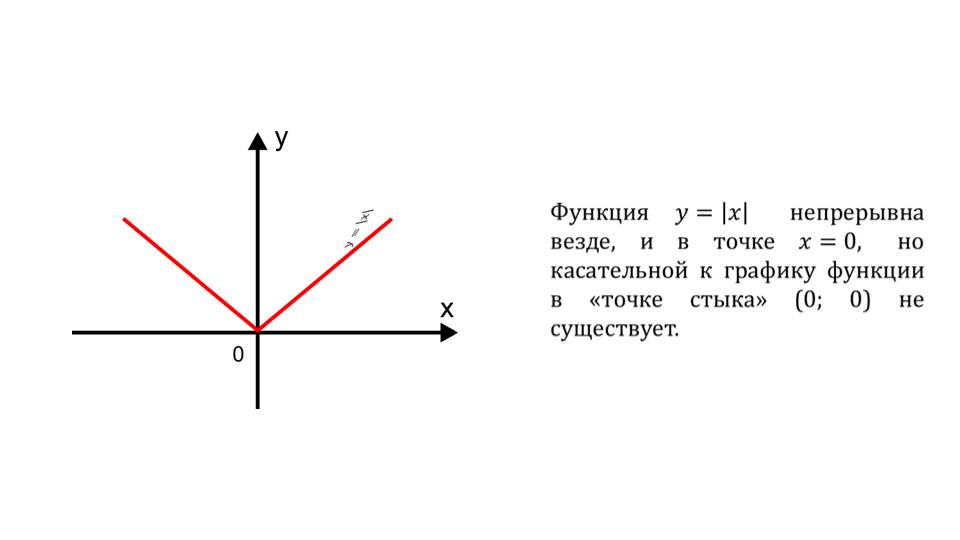
На слайде 12 рассматривается функция у=|x|. Отмечается, что данная функция непрерывна везде, однако касательной в точке (0,0) не существует. Исследование сопровождается построением графика на рисунке.


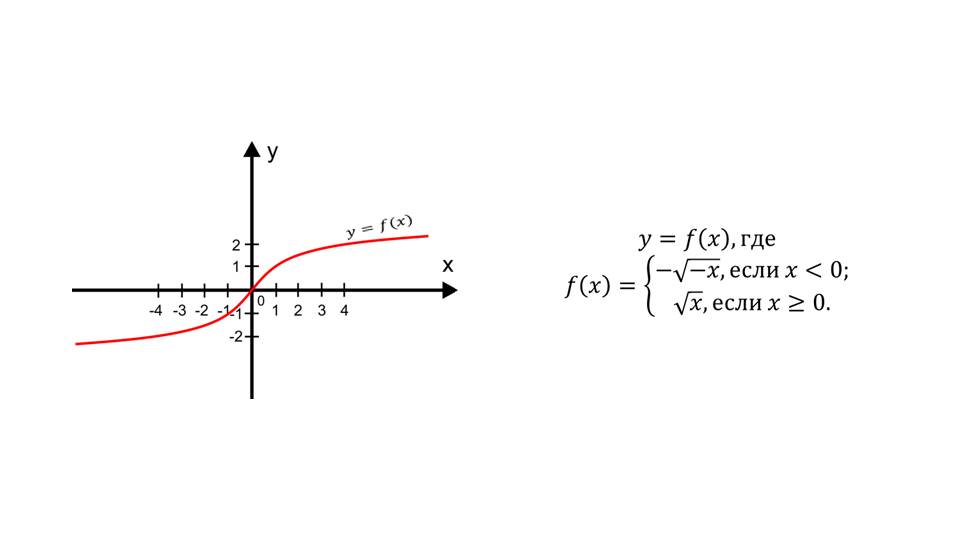
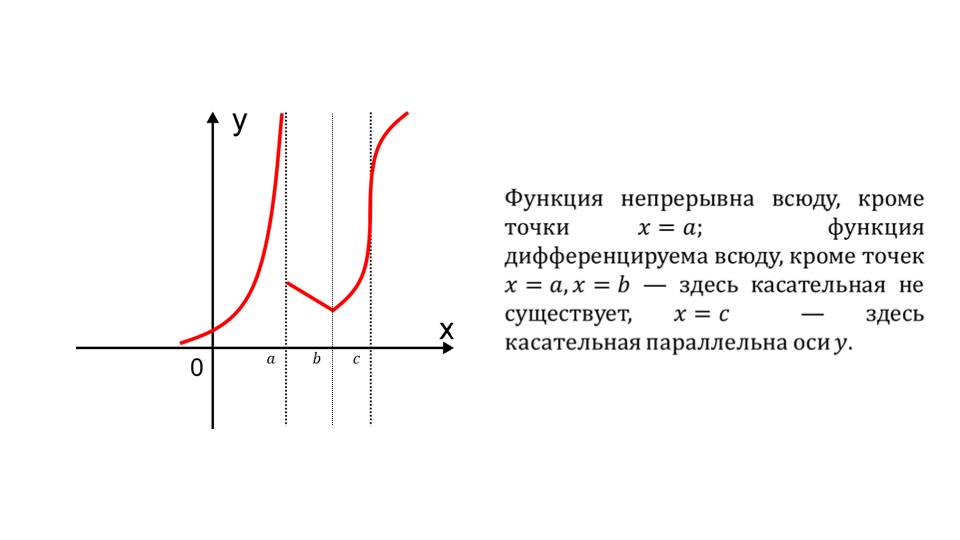
Слайд 13 демонстрирует поведение функции f(x)=-√-xдля х<0 и √х для х>=0. Также на слайде 14 продемонстрирована функция, представленная графически, которая непрерывна на числовой прямой, кроме точек х=а и х=b. Отмечается, что в точке х=С касательная к графику параллельна оси у.


Презентация «Определение производной» рекомендуется как наглядное пособие, сопровождающее объяснение учителя на традиционном уроке математики. Также материал может быть полезен учителю, осуществляющему дистанционное обучение.

Пособие может быть рекомендовано ученику, желающему лучше разобраться в предмете, для самостоятельной работы.
| Автор | |
|---|---|
| Дата добавления | 27.07.2014 |
| Раздел | Алгебра |
| Подраздел | Презентация |
| Просмотров | 7818 |
| Номер материала | 818 |