
Презентация "Параллелепипед"

Краткое описание документа:
Презентация «Параллелепипед» представляет наглядный учебный материал, который поможет учителю в достижении целей урока геометрии по данной теме. Параллелепипед является объемным телом, представление которого на плоскости имеет определенные сложности, поэтому обучение с помощью доски и мела недостаточно эффективно. Учителю необходим материал, который демонстрирует особенности объемного тела, помогает учителю донести свойства объемных тел ученикам. Презентация является наиболее удобной формой наглядного пособия. В ней можно разместить иллюстрации, четко и понятно произвести построения, вычленить элементы объемного тела.
В ходе презентации ученикам демонстрируются примеры предметов, встречающихся в практике, форма которых представляет собой параллелепипед. Представлены элементы параллелепипеда, варианты его изображения на плоскости, основные свойства, знание которых необходимо при решении задач и пример решения задачи, в которой фигурирует параллелепипед. С помощью наглядного пособия учитель может более эффективно решить задачи обучения. Применение презентации способствует запоминанию информации, удержанию внимания учеников на изучении предмета, более глубокому пониманию учебного материала.

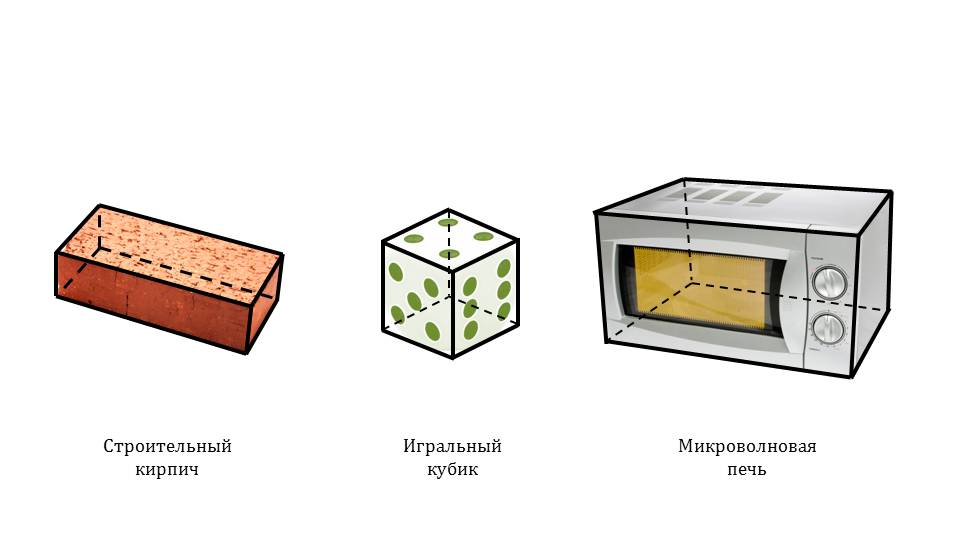
Презентация начинается с представления предметов, форма которых представляет собой параллелепипед. Для этого на слайде представлены строительный кирпич, игральный кубик и микроволновая печь. На следующем слайде наведены жирными линиями очертания представленных предметов. При этом стороны, не видные под углом обзора обозначены пунктирной линией. Данные очертания ученикам напоминают уже известную им форму параллелепипеда.
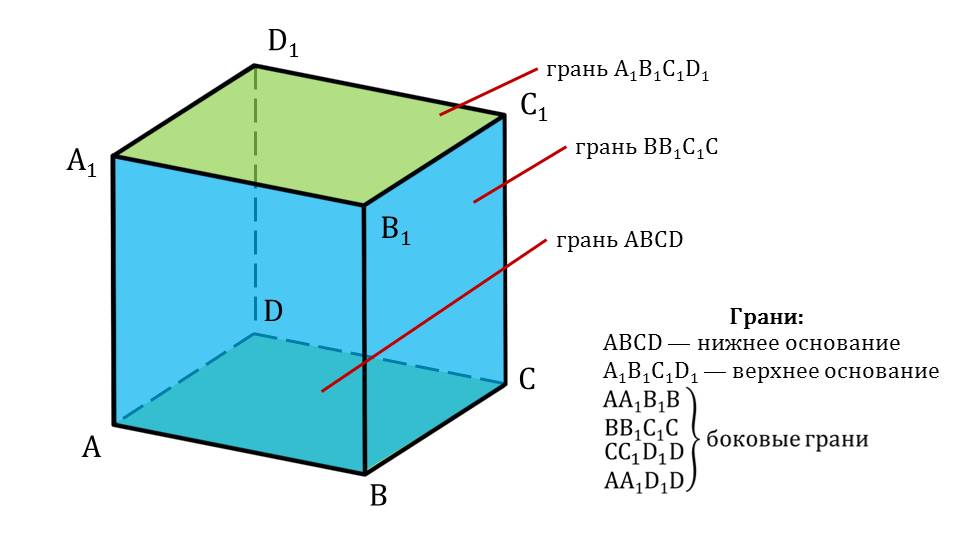
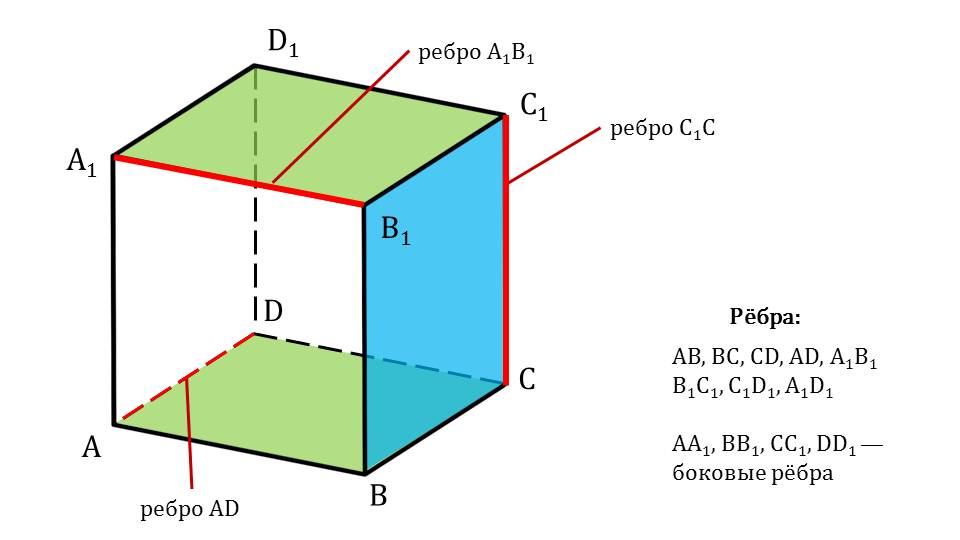
На слайде 5 представлен параллелепипед ABCDA1B1C1D1, который разбирается на элементы. С помощью цвета выделены отдельные грани, нижняя и верхняя из которых являются основаниями и выкрашены в зеленый цвет. Это грани ABCD и A1B1C1D1. При этом грани AA1B1B, BB1С1С, СС1D1D, AA1D1D являются боковыми гранями. Это отмечено также рядом с рисунком. На слайде 6 нарисован параллелепипед, в котором красным цветом выделены отрезки AD, A1B1, СС1. С помощью указателей выведено название данных отрезков – ребра параллелепипеда, среди которых AA1, BB1, СС1, DD1 – боковые ребра. Также рядом с рисунком перечислены все ребра данного параллелепипеда.
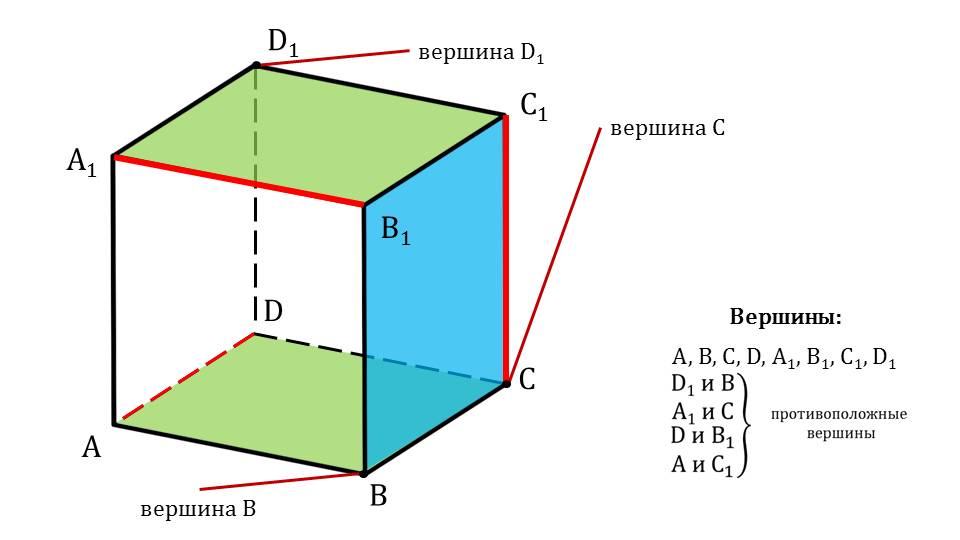
На следующем слайде на параллелепипеде отмечаются вершины. Рядом с рисунком перечислены все имеющиеся в фигуре вершины. Также отмечены противоположные вершины и рядом с рисунком перечислены все пары противоположных вершин.
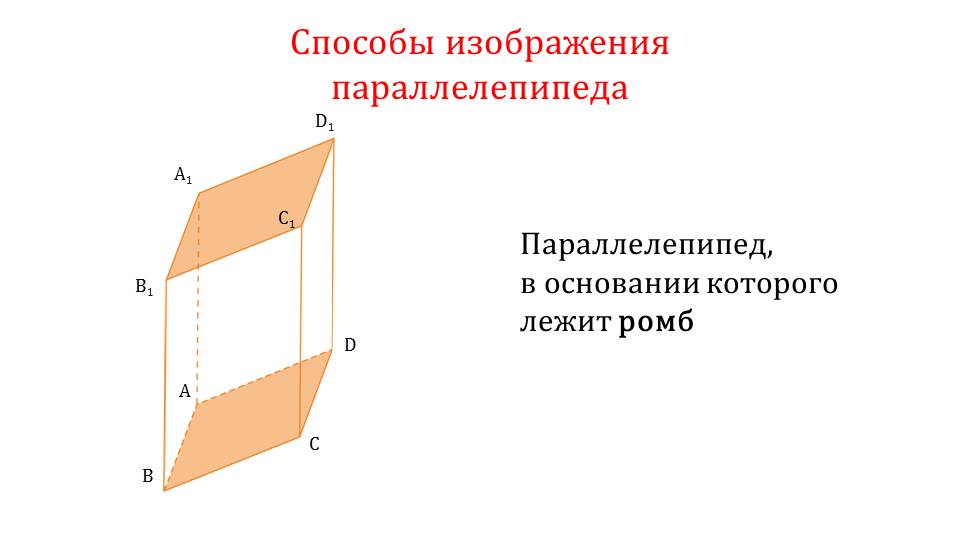
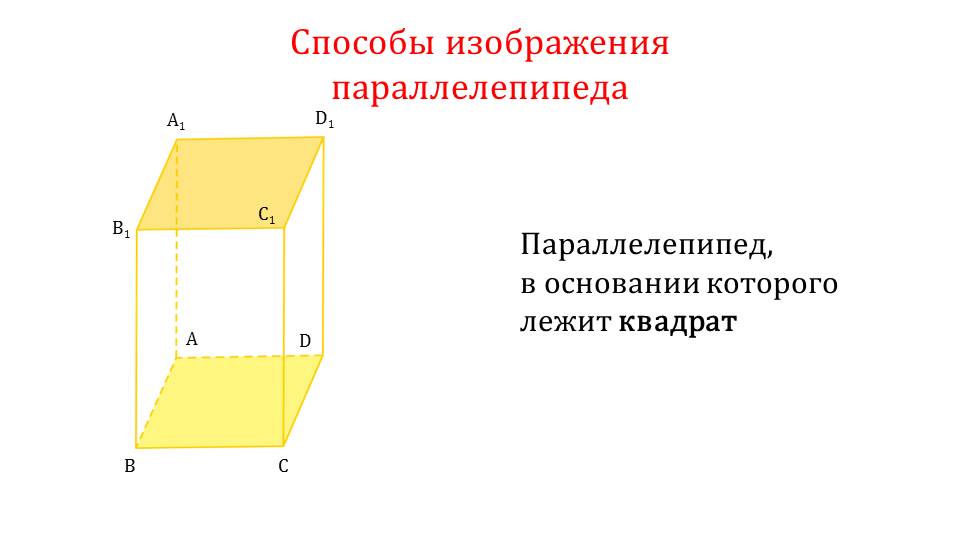
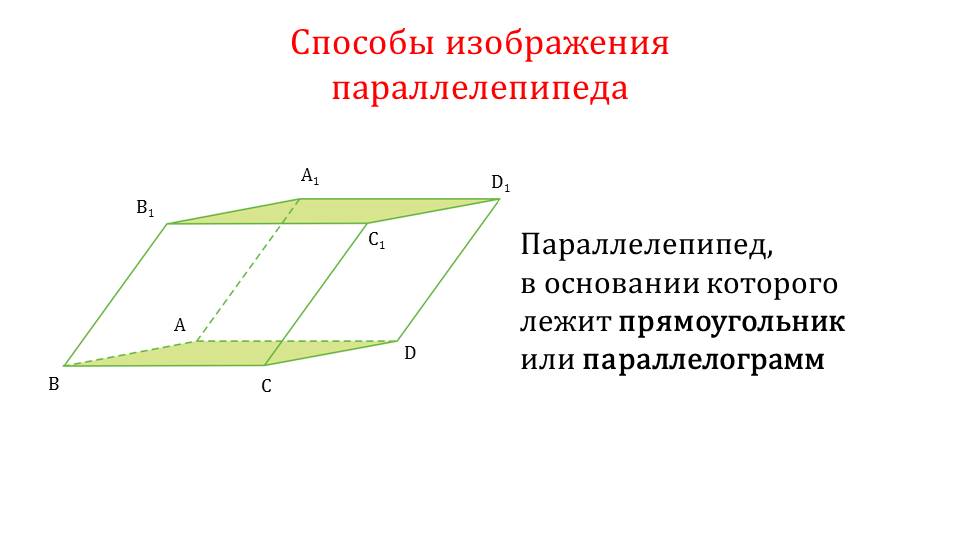
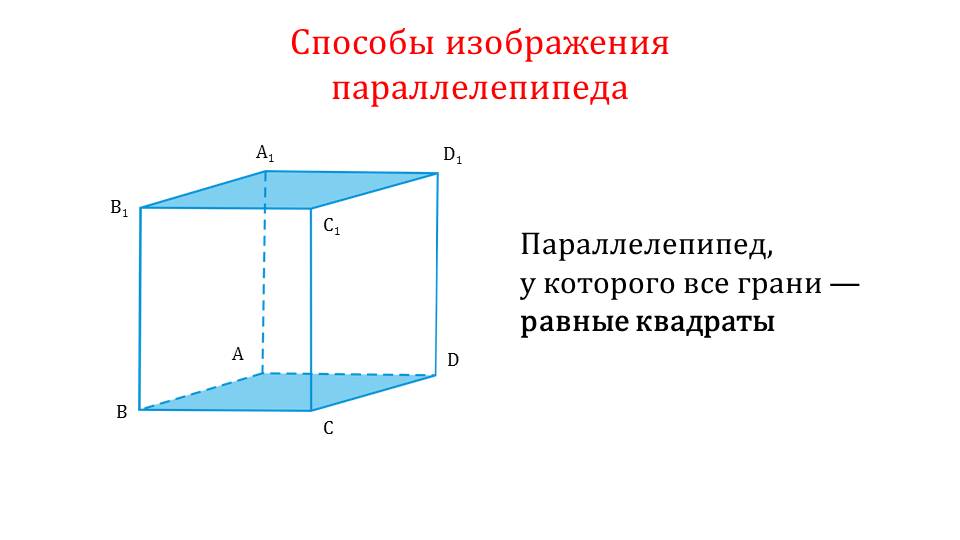
Далее демонстрируются способы изображения параллелепипеда. На слайде 8 параллелепипед, в основе которого лежит ромб, изображен, начиная с построения двух одинаковых ромбов. Вершины этих ромбов соединяются отрезками. В изображенном таким образом параллелепипеде ребра, которые не видны, отмечены пунктиром. На следующем слайде изображен параллелепипед, основа которого – квадрат. Для построения параллелепипеда, аналогично предыдущему построению, строятся основания (в данном случае квадраты), а затем их вершины соединяются отрезками. Невидимые ребра отмечаются пунктирной линией. На слайде 10 изображен параллелепипед, основание которого – прямоугольник или параллелограмм. Построение начинается также с построения равных оснований, соответствующие вершины которых соединены между собой отрезками, образуя объемную фигуру. Также невидимые линии отмечены пунктиром. Последний пример изображения параллелепипеда демонстрирует построение параллелепипеда, все грани которого равны и являются квадратами. Построение выполняется аналогично предыдущим построениям. Таким образом, приведены виды всех возможных параллелепипедов и объяснен способ их построения при выполнении практических задач.
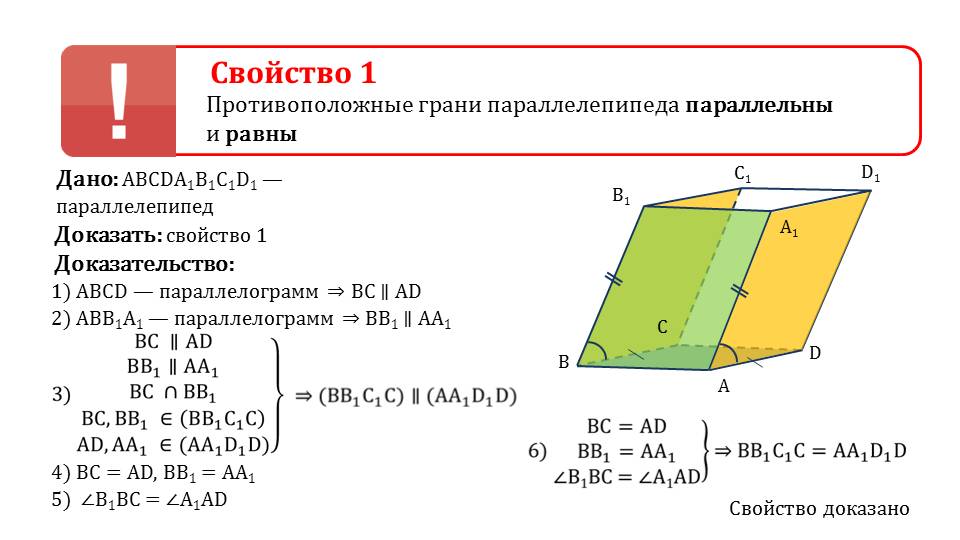
На слайде 12 демонстрируется важное свойство параллелепипеда, которое заключается в утверждении о равенстве и параллельности противоположных граней. Для доказательства свойства под формулировкой теоремы выполняется рисунок параллелепипеда ABCDA1B1C1D1. Из того, что данная фигура параллелограмм, следует параллельность ребер BC и AD, а также BB1 и AA1. Также отмечено, что ВС и ВВ1 принадлежат параллелограмму ВВ1С1С, а AD, AA1 принадлежат параллелограмму АА1D1D. Из данных условий следует параллельность параллелограммов ВВ1С1С и АА1D1D. Отмечается равенство ребер ВС=AD, ВВ1=АА1. Очевидно, равными будут и углы ∠ В1ВС=∠ А1АD. На основе указанных равенств можно сделать вывод и о равенстве параллелограммов ВВ1С1С = АА1D1D. Таким образом можно доказать и равенство всех противолежащих параллелограммов. Свойство доказано.
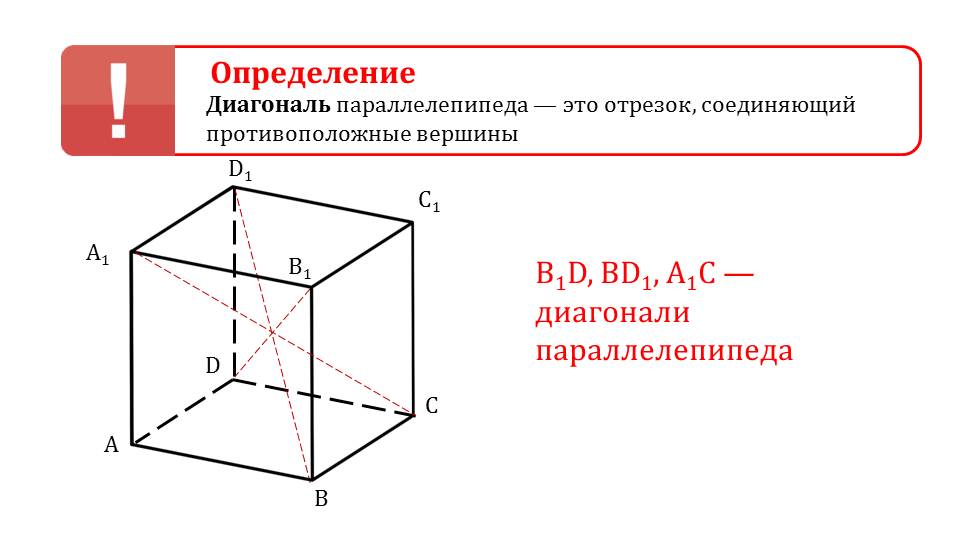
Далее дается определение диагонали параллелепипеда как отрезка, соединяющего противоположные вершины. На рисунке изображен параллелепипед, в котором проведены все диагонали, обозначенные пунктиром. Рядом с рисунком перечислены проведенные диагонали параллелепипеда B1D, BD1, A1C.
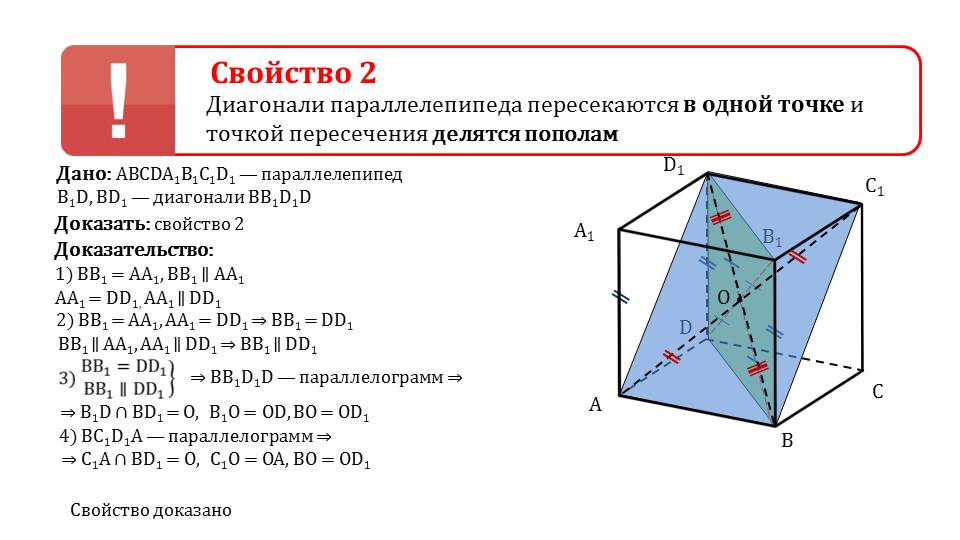
На слайде 14 представлено второе свойство параллелепипедов о пересечении всех диагоналей параллелепипеда в одной точке. Этой точкой диагонали делятся на равные части. Для доказательства данного утверждения построен параллелепипед, в котором проведены диагонали. При рассмотрении двух диагоналей АС1 и ВD1 отмечается, что они также являются диагоналями параллелограмма, построенного на основе противолежащих вершин АВС1D1. По свойству параллелограмма диагонали точкой пересечения делятся пополам. Таким же образом можно доказать данное свойство для пары любых двух диагоналей. Свойство доказано.
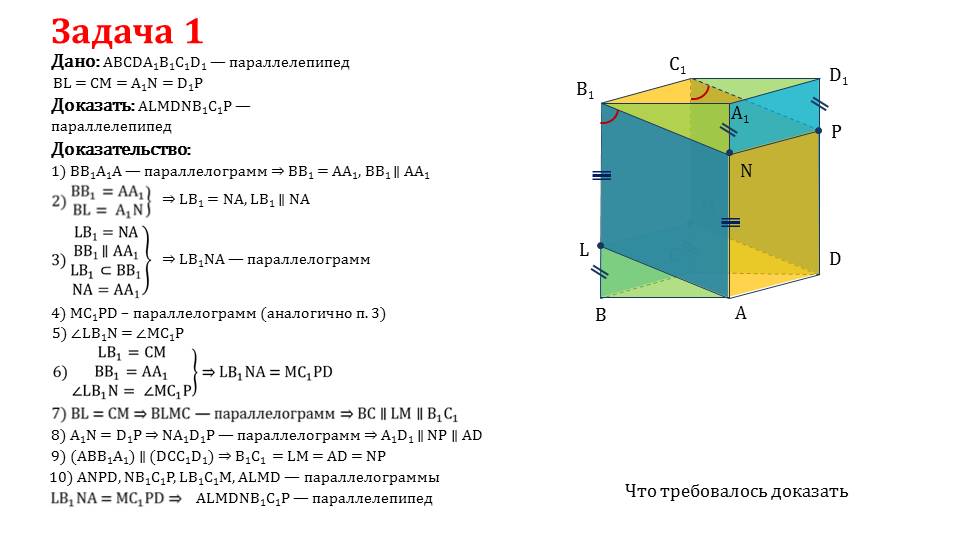
На последнем слайде представлено описание решения задачи, в которой дан параллелограмм ABCDA1B1C1D1. При смещении ребра ВС вверх на высоту BL и опускания A1D1 на такую же величину A1N образуется новая фигура. Необходимо доказать, что это параллелепипед. Доказательство выполняется, используя свойства параллелограммов, которыми являются грани параллелепипеда. Учитывая равные расстояния, на которые смещаются ребра параллелепипеда, доказывается, что все образованные грани новой фигуры также являются параллелограммами. А фигура, составленная из шести параллелограммов, является параллелепипедом. Утверждение доказано.
Презентация «Параллелепипед» применяется на уроке геометрии в школе для обеспечения наглядности объяснения учителя. Также данный наглядный материал может быть полезен учителю, осуществляющему дистанционное обучение. Для углубления понимания предмета изучения презентация может быть рекомендована ученику для самостоятельного рассмотрения.
| Автор | |
|---|---|
| Дата добавления | 28.10.2014 |
| Раздел | Геометрия |
| Подраздел | Презентация |
| Просмотров | 7624 |
| Номер материала | 885 |