
Презентация "Переход к новому основанию логарифма"

Краткое описание документа:
Не существует единого стандарта при решении всех математических задач. Иногда требуется выполнить дополнительные действия, которые поспособствуют быстрому и правильному решению задачи. При работе с логарифмическими уравнениями очень часто необходимо привести основание к другому значению. Но как это сделать – ведь нельзя произвольно менять основание на удобное для ученика значение?
Презентация «Переход к новому основанию логарифма» поможет найти ответ на этот вопрос.

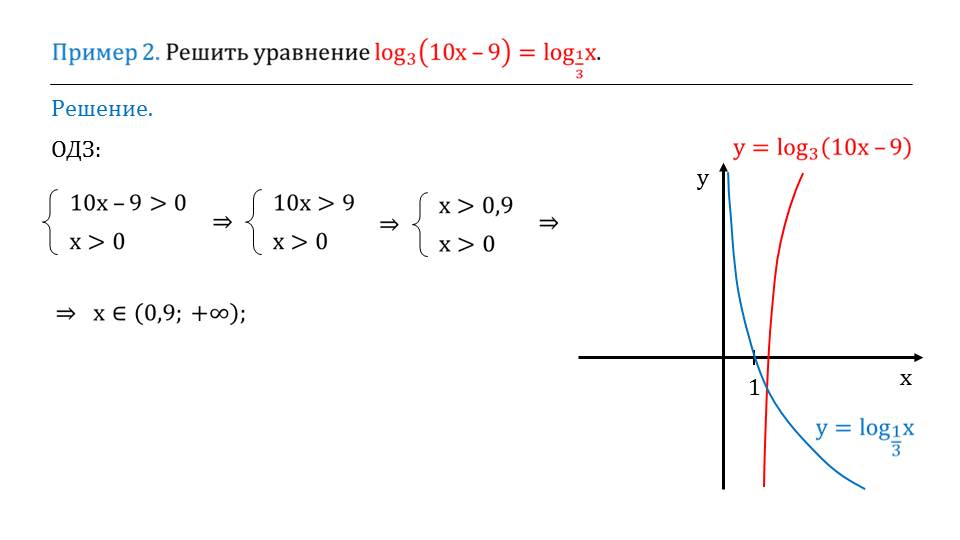
Сама презентация построена несколько необычно, так как предлагает начать тему с практической части, а не с теоретической, что является более традиционным способом подачи информации. Урок начинается с разборки двух примеров, которые предлагают ознакомиться со способами решения задач, в которых, по условию, разные показатели степени или разные основания в каждой логарифмической функции.
После рассмотрения предоставленных примеров, ученикам предлагается теорема, позволяющая заменить одну логарифмическую функцию на результат деления других, но с другим основанием. Логическим продолжением этого правила идет доказательство, которое демонстрируется с помощью математических действий над предложенным логарифмом.


Многие математические теоремы имеют так называемые следствия, которые более обширно раскрывают суть определения, позволяя ученикам не делать дополнительных, лишних шагов при каждом решении задачи. Предложенная в презентации теорема также имеет следствия, которые, в количестве двух штук, а также их доказательство, предложены к ознакомлению в следующей части урока. Каждое из следствий рассматриваемых в теме имеют вид не только правила, но и отдельной математической формулы, которые демонстрируются на следующем слайде презентации «Переход к новому основанию логарифма».


Естественно, что любая формула или правило требует практического освоения, которое способствует более быстрому запоминанию нового материала. Поэтому заключительная часть презентации предлагает ознакомиться ученикам с решением трех примеров, в которых используется метод замены основания у логарифма. Задачи, предложенные в практическом уроке, построены таким образом, чтобы учащиеся смогли научиться решать логарифмические уравнения новым способом, проводить вычисления, а также получить понятие о замене математических чисел на буквенные аналоги.


Логическим итогом презентации «Переход к новому основанию логарифма» является последний слайд, который дублирует формулы, полученные ранее из основной теоремы заданной темы.
Отличием презентации от любого учебного материала, предлагаемого школьным учебником, является более качественная подача информации, которая осуществляется за счет оформления наиболее важных частей темы отдельными слайдами, не позволяющих распылять внимание ученика на посторонние вещи, а также выделение наиболее значимых формул и определений другими, более яркими цветами и оформления их в рамки.


Презентация «Переход к новому основанию логарифма» завершает собой тему, посвященную обычной логарифмической функции. Изучение всего предложенного материала особенно важно перед началом следующего курса школьной программы, который ознакамливает учащихся с натуральными логарифмами, понять которые без предыдущей темы – невозможно.

Логарифмы, такие незаметные в повседневной жизни, имеют важное практическое значение во многих технических профессиях. Учитывая развитие цивилизации именно в этом направлении, можно с уверенностью сказать, что знание логарифмической функции, а также умение работать с ней при решении различных задач, поможет ученикам, решившим посвятить себя изучению точных наук в дальнейшем.
| Автор | |
|---|---|
| Дата добавления | 16.11.2014 |
| Раздел | Алгебра |
| Подраздел | Презентация |
| Просмотров | 8200 |
| Номер материала | 1031 |