
Презентация «Перестановки»

Краткое описание документа:
Презентация «Перестановки» представляет учебный материал для школьного урока по данной теме. Презентация содержит определение перестановок, наглядные примеры для понимания смысла данной операции, описание математического аппарата для решения задач с перестановками, примеры решения задач. Задача презентации – в удобной, понятной форме донести до учеников учебный материал, способствовать лучшему его пониманию и запоминанию.


В презентации используются специальные приемы, помогающие учителю объяснить новую тему. Учебные материалы заранее структурированы. При помощи анимационных эффектов они представляют примеры и задачи, делая акценты на важные особенности примеров и задач при демонстрации. Важные понятия выделяются цветом, что облегчает их запоминание.
После представления темы урока ученикам демонстрируется определение перестановок как простейших комбинаций, которые можно составить из некоторого множества элементов. Текст выделен знаком восклицания как важный для запоминания.

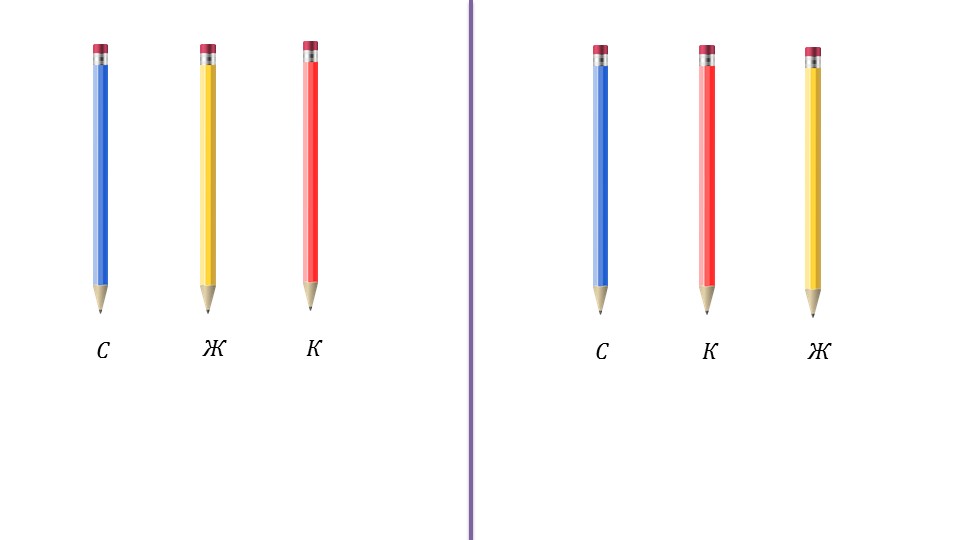
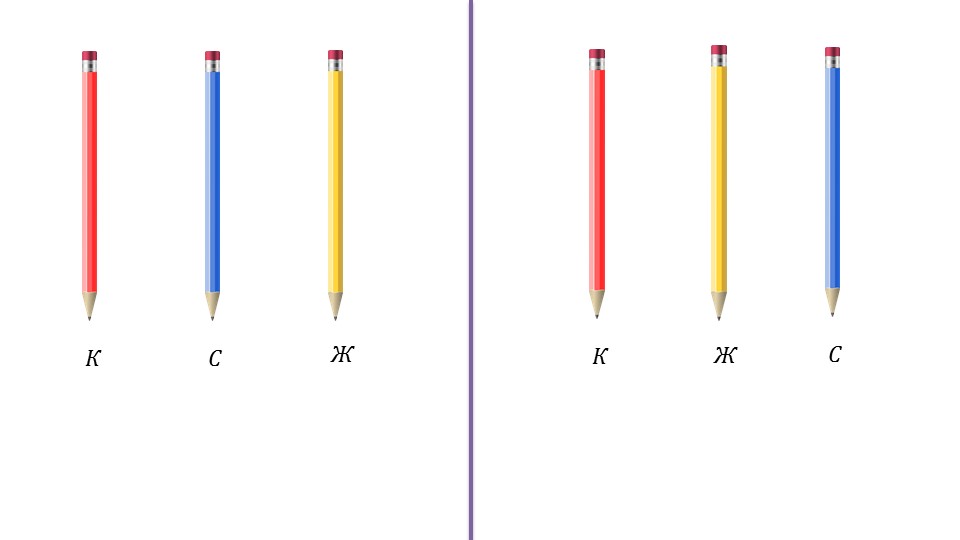
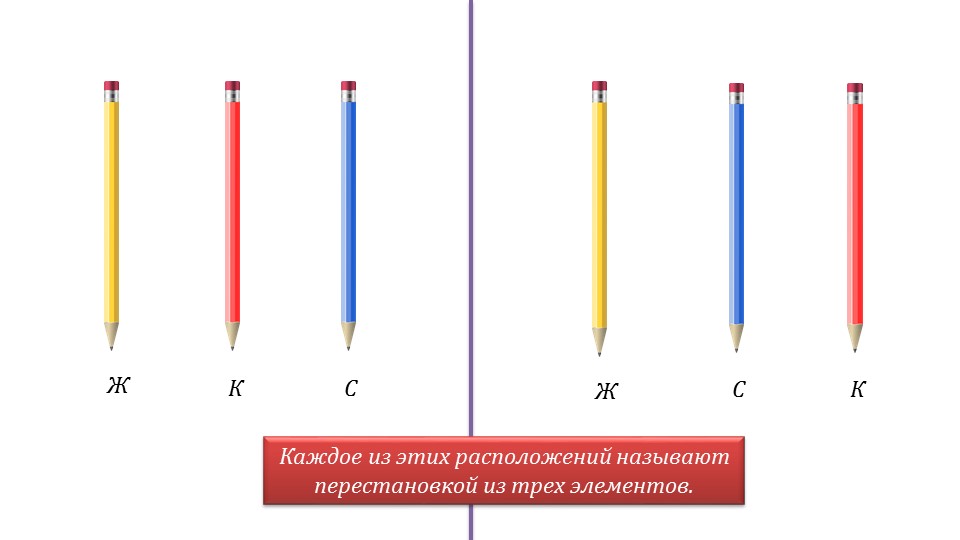
Далее демонстрируется пример перестановок на цветных карандашах, которые можно разместить в различном порядке. Для этого карандаши подписываются первой буквой названия их цвета: С, К, Ж. При помощи анимированного представления наглядно демонстрируются варианты размещения данных карандашей по порядку. На одном слайде первыми размещаются синие карандаши, а рядом с ними два варианта размещения – красный и желтый, желтый и красный. На следующем слайде продемонстрированы варианты размещения карандашей после красного – синий и желтый, желтый и синий. Последние возможные варианты – после желтого красный и синий, синий и красный. После наглядной демонстрации выполненные операции подписываются как перестановки из трех элементов. Более точное определение перестановки из трех элементов дается на отдельном слайде 7. В рамке для запоминания выделен текст, что каждое расположение данных элементов в определенном порядке будет называться перестановкой из трех элементов.
На слайде 8 продемонстрировано обозначение перестановок из n элементов - Pn. Указано, что перестановки из трех элементов были подробно рассмотрены на примере карандашей, при этом очевидно, что таких перестановок будет 6. На слайде отмечена математическая запись количества перестановок: P3=6. Далее на экране отмечается, что для нахождения количества перестановок из трех элементов существует комбинаторное правило умножения.


На следующем слайде процедура перестановок раскладывается на этапы, чтобы получить правило для нахождения количества перестановок. Указано, что для подсчета необходимо на первое место ставить любой из трех элементов. Для него есть две возможности выбрать второй элемент. Для выбора третьего элемента остается единственная возможность. Это означает, что количество перестановок из 3 элементов будет находиться перемножением 3•2•1=6. Получаем общее число возможных вариантов перестановок. Аналогично процессу поиска вариантов перестановок рассматривается вариативность для n элементов.


Пусть есть некоторое множество n элементов. Для него на второе место помещается один из n-1 элементов, на третье место соответственно помещается один из n-2 элементов и т.д. Таким образом, можно вывести общее правило для поиска числа перестановок из n элементов: Pn=n(n-1)(n-2)•…•3•2•1.
На слайде 11 на экран выведена формула Pn в виде Pn=1•2•3•…•(n-2)(n-1)n. Таким образом вводится понятие факториала, обозначение которого продемонстрировано ниже формулы: n!. Рассмотрены примеры нахождения факториала от некоторого числа: 3!=1•2•3=6, а также 6!=1•2•3•4•5•6=720. Также указано, что 1!=1. Текст общего правила нахождение количества перестановок как n факториала расположен внизу слайда.
Далее предлагается рассмотреть несколько задач на нахождение числа перестановок. На слайде 12 предлагается к решению задача на нахождение количества способов разложения семи шаров по семи ячейкам. Указано, что способом решения является вычисление числа перестановок из 7 элементов: P7=7!=5040.


На слайде 13 рассматривается решение задачи на нахождение количества четырехзначных чисел, которые составлены из 0,1,2,3, при этом цифры в одном числе не повторяются. Решение предусмотрено в два этапа – сначала находится число всех перестановок из 4 элементов, а затем из них вычитается число перестановок, в которых числа с 0 впереди, так числа, начинающиеся с нуля, не будут четырехзначными. Таким образом, решение сводится к вычислению P4-P3=4!-3!=18. То есть вариантов образования таких чисел - 18.
На последнем слайде рассматривается решение задачи, в которой предлагается найти количество способов, которыми можно расставить 9 тарелок, 4 из которых – красные, так, чтобы красные располагались рядом. Основная трудность в решении данной задачи – понять, что красные тарелки в данных перестановках необходимо принимать за одну. Таким образом, решение сводится к нахождению произведения P6•P4=6!•4!=17280.


Презентация «Перестановки» предназначена для наглядного сопровождения объяснения учителя по теме «Перестановки». Подробное понятное представление учебного материала может быть также полезно при дистанционном обучении, а рассмотренные при этом задачи помогут ученику разобраться с решением самостоятельно.
| Автор | |
|---|---|
| Дата добавления | 29.08.2014 |
| Раздел | Алгебра |
| Подраздел | Презентация |
| Просмотров | 8811 |
| Номер материала | 649 |