
Презентация "Показательная функция, ее свойства и график"

Краткое описание документа:
Презентация «Показательная функция, ее свойства и график» наглядно представляет учебный материал по данной теме. В ходе презентации подробно рассматриваются свойства показательной функции, ее поведение в системе координат, рассматриваются примеры решения задач с использованием свойств функции, уравнений и неравенств, изучаются важные теоремы по теме. С помощью презентации учитель может повысить эффективность урока математики. Яркое представление материала помогает удерживать внимание учеников на изучении темы, анимационные эффекты помогают более понятно продемонстрировать решения задач. Для более быстрого запоминания понятий, свойств и особенностей решения используется выделение цветом.
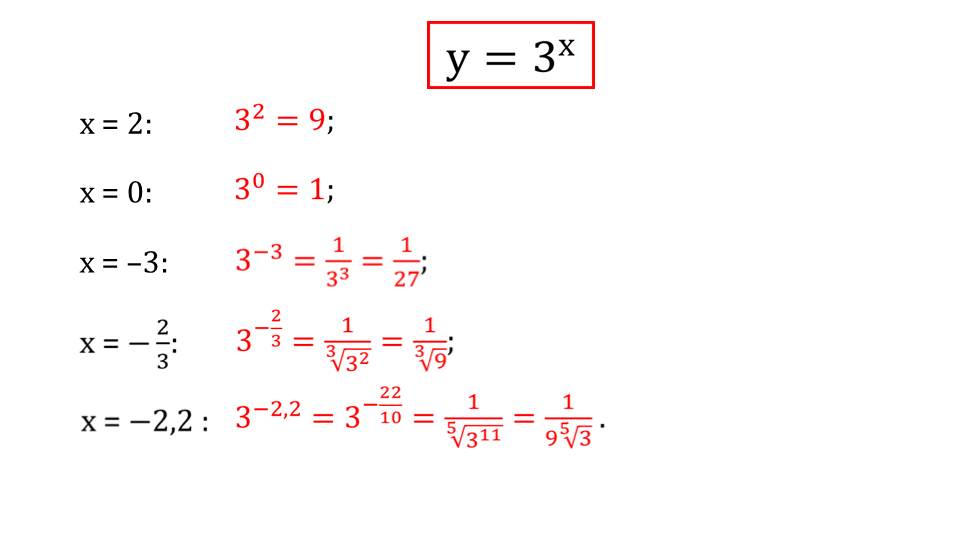
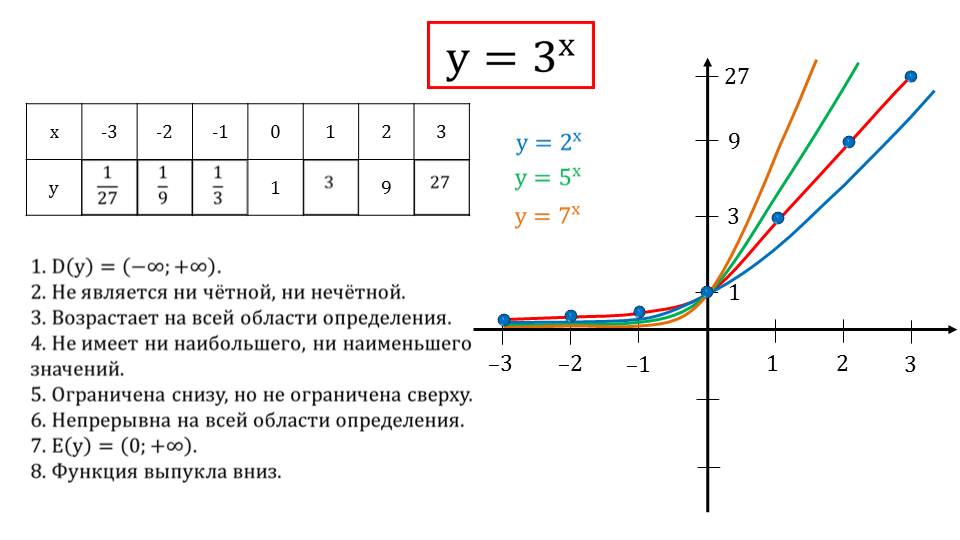
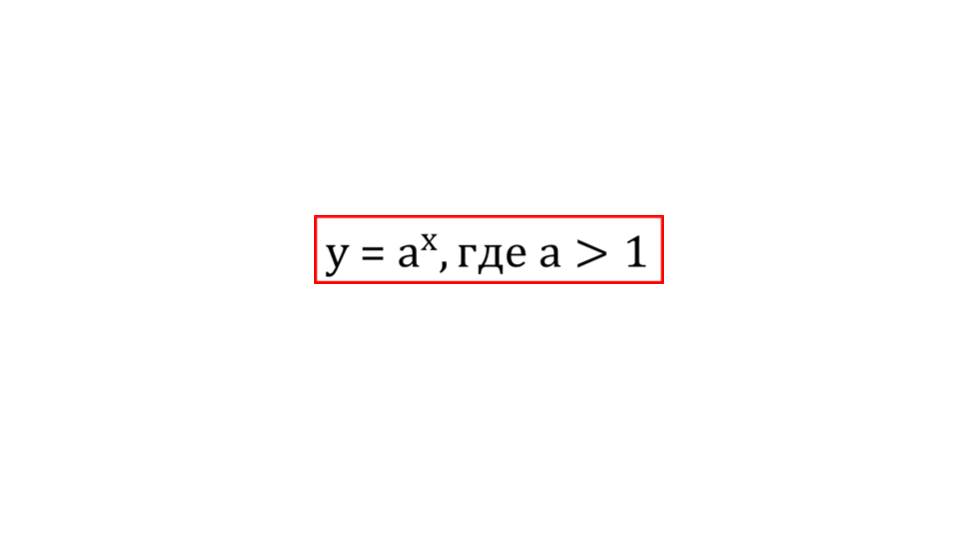
Демонстрация начинается с примеров показательной функции у=3х с различными показателями – целыми положительными и отрицательными, обыкновенной дробью и десятичной. Для каждого показателя вычисляется значение функции. Далее для этой же функции строится график. На слайде 2 построена таблица, заполненная координатами точек, принадлежащих графику функции у=3х. По этим точкам на координатной плоскости строится соответствующий график. Рядом с графиком строятся аналогичные графики у=2х, у=5х и у=7х. Каждая функция выделена разными цветами. В таких же цветах выполнены графики этих функций. Очевидно, что с ростом основания степени показательной функции график становится круче и больше прижимается к оси ординат. На этом же слайде описаны свойства показательной функции. Отмечается, что областью определения является числовая прямая (-∞;+∞), Функция не является четной или нечетной, на все области определения функция возрастает и не имеет наибольшего или наименьшего значения. Показательная функция ограничена снизу, но не ограничена сверху, непрерывна на области определения и выпуклая вниз. Область значений функции принадлежит промежутку (0;+∞).



Далее демонстрируется общий вид показательной функции у=ах для положительного а. Общий вид функции выделен в рамку, чтобы легче запоминался.
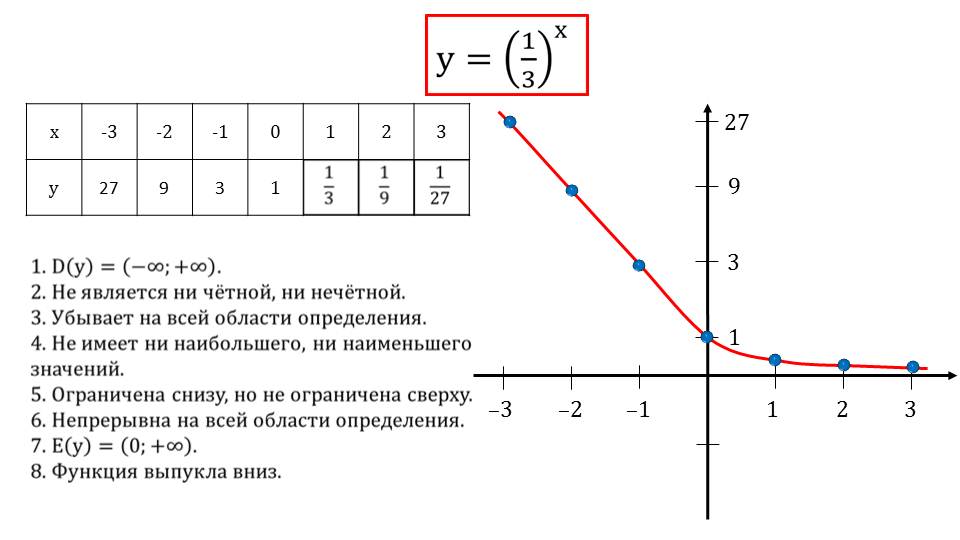
На слайде 4 представлено исследование функции у=(1/3)х. Строится график функции. Для этого заполняется координатами точек, принадлежащих графику функции, таблица. По этим точкам строится график на прямоугольной системе координат. Рядом описываются свойства функции. Отмечается, что областью определения является вся числовая ось. Эта функция не является нечетной или четной, убывающая на всей области определения, не имеет наибольшего, наименьшего значений. Функция у=(1/3)х является ограниченной снизу и неограниченной сверху, на области определения непрерывна, имеет выпуклость вниз. Область значений – положительная полуось (0;+∞).
На приведенном примере функции у=(1/3)х можно выделить свойства показательной функции с положительным основанием, меньшим единицы и уточнить представление о ее графике. На слайде 5 представлен общий вид такой функции у=(1/а)х, где 0<a<1. Под общим видом описывается исследование такой функции. Оно совпадает со свойствами, указанными в исследовании у=(1/3)х.
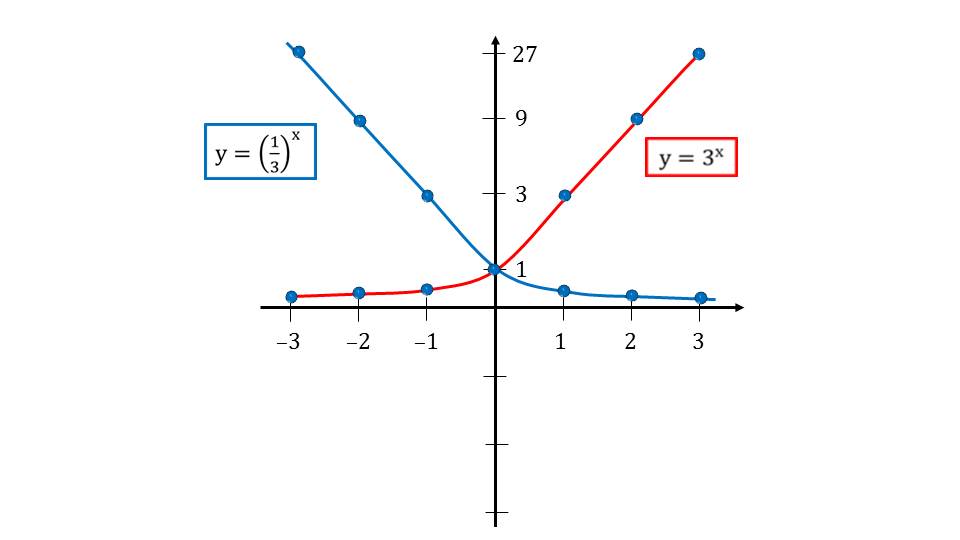
На слайде 6 сравниваются графики функций у=(1/3)х и у=3х. Видно, что эти графики симметричны относительно оси ординат. Чтобы сравнение было более наглядным, графики окрашены в цвета, которыми выделены формулы функций.
Далее представляется определение показательной функции. На слайде 7 в рамке выделено определение, в котором указано, что функция вида у=ах, где положительное а, не равное 1, называется показательной. Далее с помощью таблицы сравнивается показательная функция с основанием, большим 1, и положительным меньшим 1. Очевидно, что практически все свойства функции аналогичны, только функция с основанием, большим а, возрастающая, а с основанием, меньшим 1, убывающая.
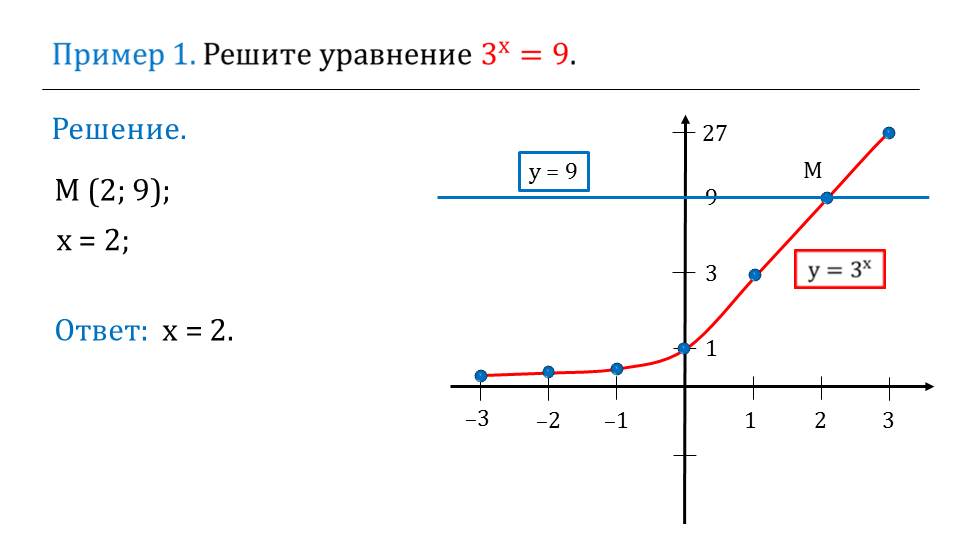
Далее рассматривается решение примеров. В примере 1 необходимо решить уравнение 3х=9. Уравнение решается графическим способом – строится график функции у=3х и график функции у=9. Точка пересечения этих графиков М(2;9). Соответственно, решением уравнения является значение х=2.
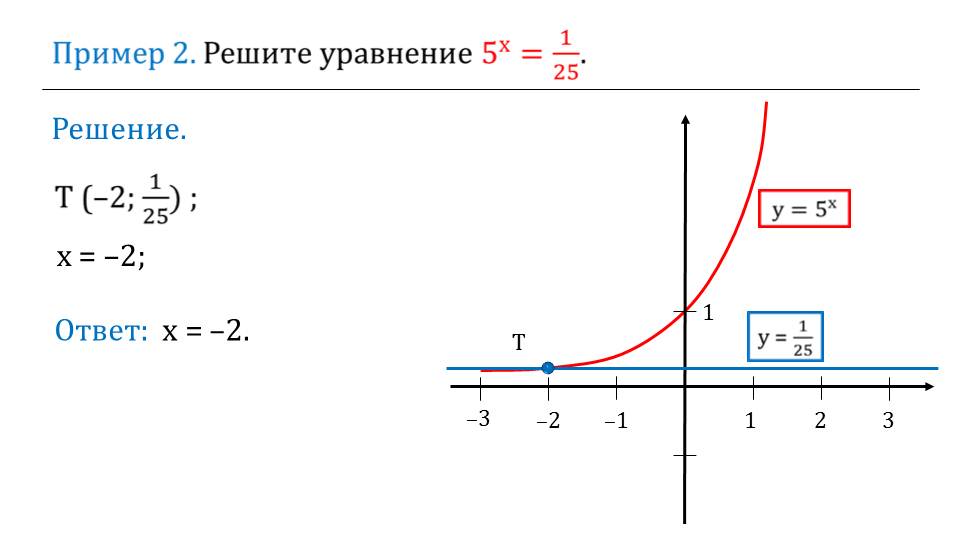
На слайде 10 описывается решение уравнения 5х=1/25. Аналогично предыдущему примеру решение уравнения определяется графически. Демонстрируется построение графиков функций у=5х и у=1/25. Точкой пересечения данных графиков является точка Е(-2;1/25), значит, решение уравнения х=-2.


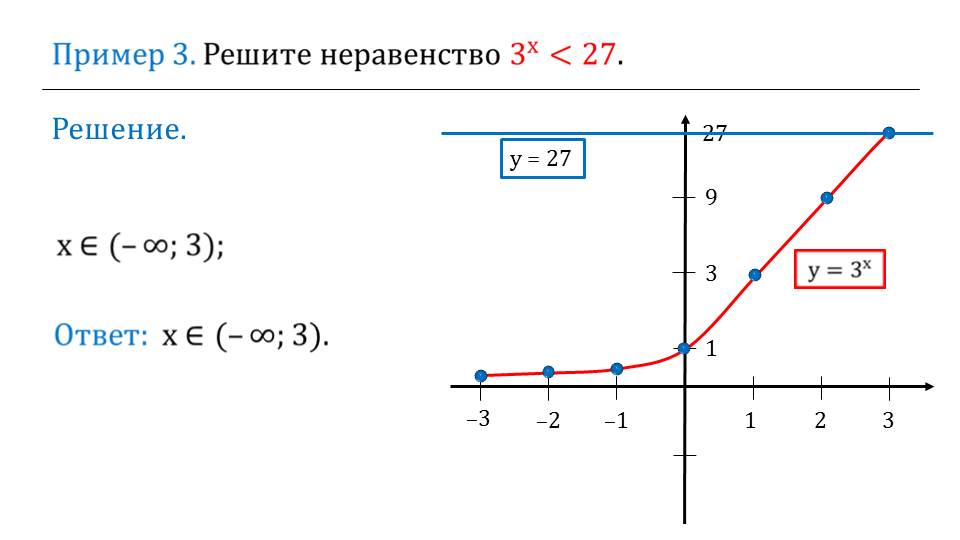
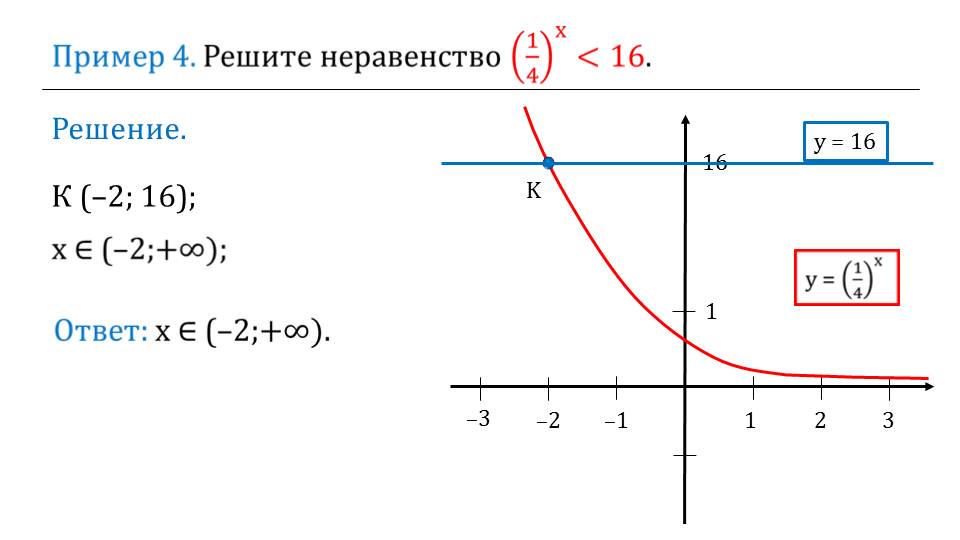
Далее предлагается рассмотреть решение неравенства 3х<27. Решение выполняется графически – определяется точка пересечения графиков у=3х и у=27. Затем на плоскости координат хорошо видно, при каких значениях аргумента значения функции у=3х будут меньшими 27 – это промежуток (-∞;3). Аналогично выполняется решение задания, в котором нужно найти множество решений неравенства (1/4)х<16. На координатной плоскости строятся графики функций, соответствующих правой и левой части неравенства и сравниваются значения. Очевидно, что решением неравенства является промежуток (-2;+∞).
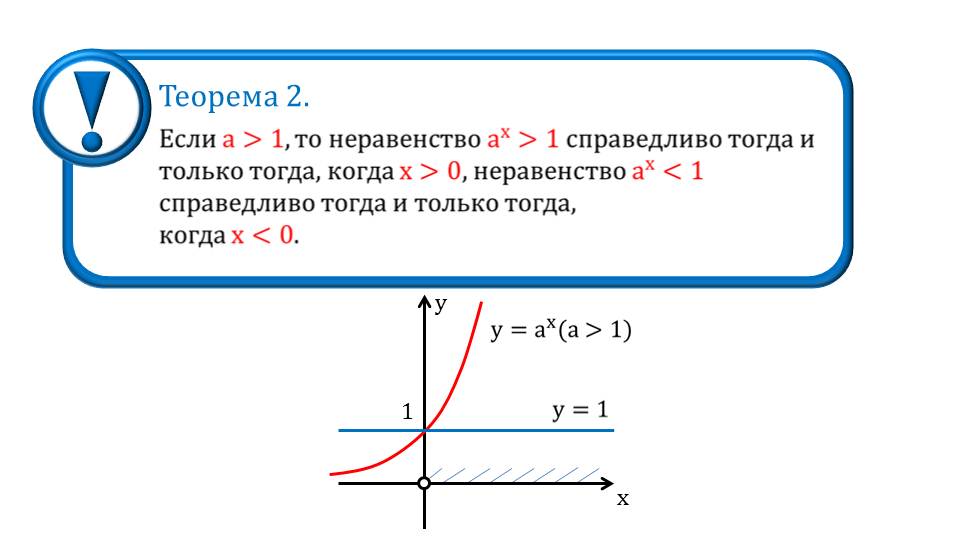
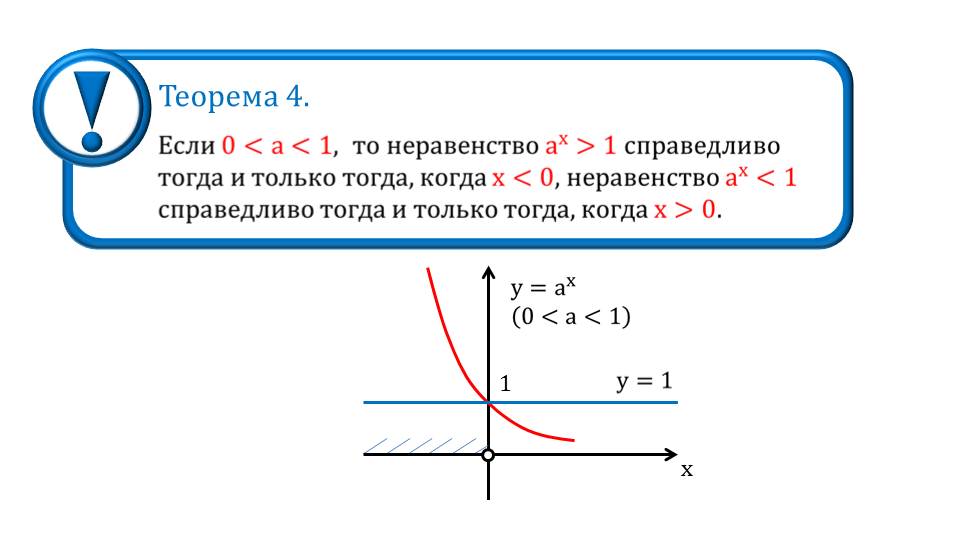
На следующих слайдах представлены важные теоремы, которые отражают свойства показательной функции. В теореме 1 утверждается, что при положительном а равенство аm=аn справедливо тогда, когда m=n. В теореме 2 представлено утверждение, что при положительном а значение функции у=ах будет больше 1 при положительном х, а меньше 1 при отрицательном х. Утверждение подтверждается изображением графика показательной функции, на котором видно поведение функции на различных промежутках области определения. В теореме 3 отмечается, что для 0<a<1 равенство аm=аn также справедливо только для m=n. Теорема 4, аналогично теореме 2, рассматривается поведение функции на координатной плоскости, но для случая 0<a<1. Отмечается, что большим 1 значение функции у=ах будет при отрицательном х, а меньшим 1 – при положительном х.
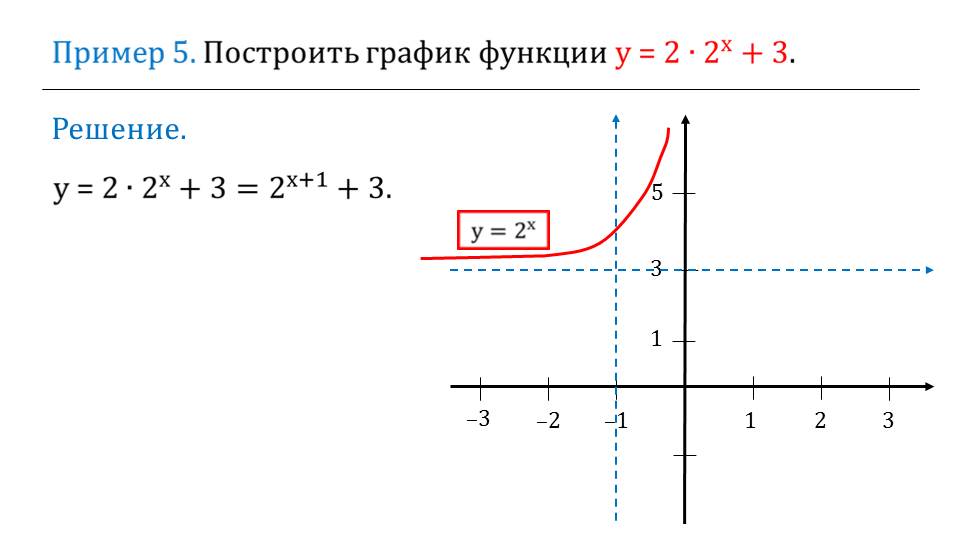
Далее для усвоения материала учениками рассматриваются примеры решения задач с использованием изученного теоретического материала. В примере 5 необходимо построить график функции у=2·2х+3. Демонстрируется принцип построения графика функции, преобразовав сначала ее в вид у= ах+а+b.Производится параллельный перенос системы координат в точку (-1;3) и относительно этого начала координат строится график функции у=2х.
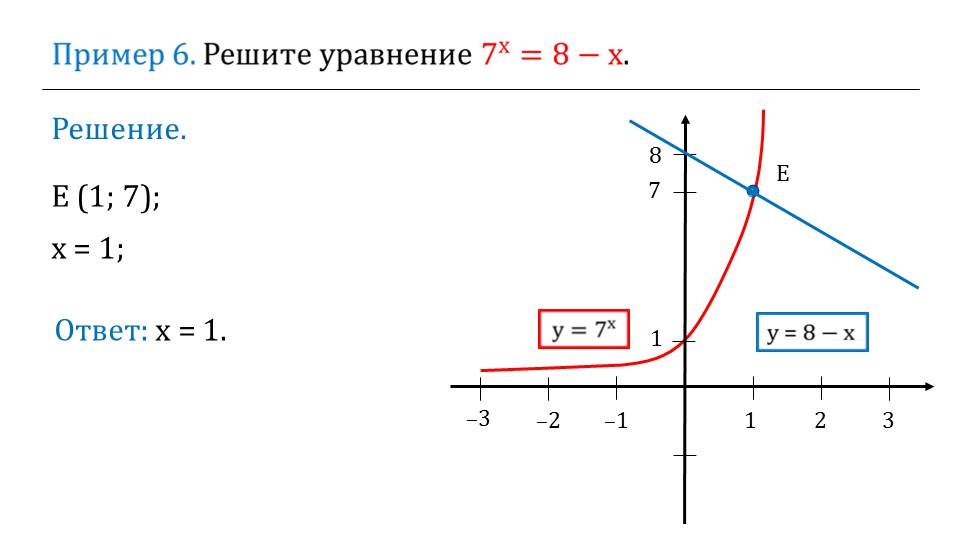
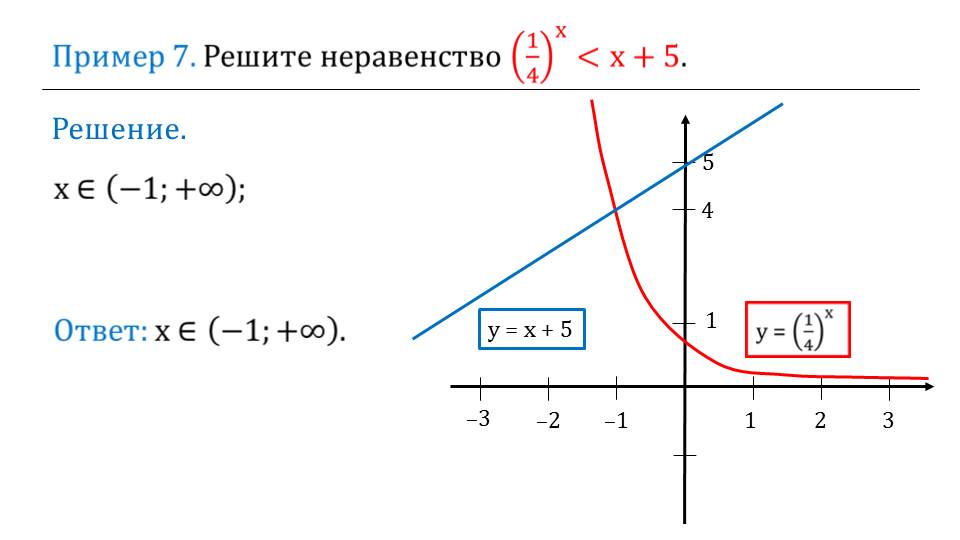
На слайде 18 рассматривается графическое решение уравнения 7х=8-х. Строится прямая у=8-х и график функции у=7х. Абсцисса точки пересечения графиков х=1 является решением уравнения. Последний пример описывает решение неравенства (1/4)х=х+5. Строятся графики обеих частей неравенства и отмечается, что его решением являются значения (-1;+∞), при которых значения функции у=(1/4)х всегда меньше значений у=х+5.
Презентация «Показательная функция, ее свойства и график» рекомендуется для повышения эффективности школьного урока математики. Наглядность материала в презентации поможет добиться целей обучения в ходе дистанционного урока. Презентация может быть предложена для самостоятельной работы ученикам, недостаточно хорошо освоившим тему на уроке.
| Автор | |
|---|---|
| Дата добавления | 16.11.2014 |
| Раздел | Алгебра |
| Подраздел | Презентация |
| Просмотров | 9237 |
| Номер материала | 1023 |