
Презентация "Показательные неравенства"

Краткое описание документа:
Презентация «Показательные неравенства» создана для наглядного представления учебного материала по данной теме. В ходе презентации представляется теоретический материал, который помогает найти способ решения показательного неравенства, рассматриваются примеры решения показательных неравенств. С помощью презентации учителю легче сформировать необходимые знания и навыки, быстрее достичь учебных целей и задач. Данная форма наглядности дает множество преимуществ, помогающих улучшить запоминание материала, углубить понимание. С этой целью используются такие приемы, как выделение цветом, анимационные эффекты, вставка рисунков, выделение текста указателями, рамкой, другими знаками.

Демонстрация начинается с определения показательного неравенства. Отмечается, что показательными неравенствами называются неравенства, имеющие вид af(x)>ag(x), где а – положительное, не равное 1, число. Во втором слайде представляется теорема, которую необходимо знать для решения показательных неравенств, и ее доказательство. В теореме утверждается, что показательное неравенство af(x) > ag(x). Является равносильным неравенству того же смысла f(x) > g(x) для а, большего 1. Также исходное неравенство будет равносильным f(x) < g(x) при положительном а, меньшем 1. Чтобы доказать данное утверждение, обе части неравенства делятся на одно и тоже число af(x)/ ag(x)> ag(x)/ ag(x). В результате деления получим неравенство af(x)/ ag(x)>1. Используя свойства частного степени, в левой части неравенства получаем af(x)-g(x)>1.
Очевидно, что при а, большем 1, данное неравенство будет равносильно f(x)-g(x)>1, то есть f(x)>g(x). При положительном а, меньшем 1, получаем равносильное неравенство f(x)-g(x)<1, то есть f(x)<g(x).

Далее рассматривается решение примеров для формирования умения решать показательные неравенства. В примере 1 требуется решить неравенство (2/3)3х+6>4/9. Чтобы решить неравенство, обе его чатси приводятся к степени с одинаковым основанием. Так как 4/9=(2/3)2, неравенство принимает вид (2/3)3х+6>(2/3)2. Так как основанием степени является число, меньшее 1, решение неравенства сводится к решению простого неравенства 3х+6<2. В результате решения неравенства получаем множество его решений (-∞;-4/3).

Для решения неравенства 2√2·2х-3> =1/2 правая часть неравенства сначала представляется в виде степени с основанием 2. То есть ½=2-1. Левую часть неравенства также необходимо преобразовать. Воспользовавшись знаниями о свойствах степеней, определяем 2√2·2х-3=2х-1,5. После подстановки преобразованных выражений в неравенство, получаем неравенство вида 2х-1,5> =2-1. Таким образом, решение показательного неравенства сводится к решению простого неравенства х-1,5> =-1. Из него находим х> =0,5, то есть множество решений находится в промежутке [0.5;+∞).

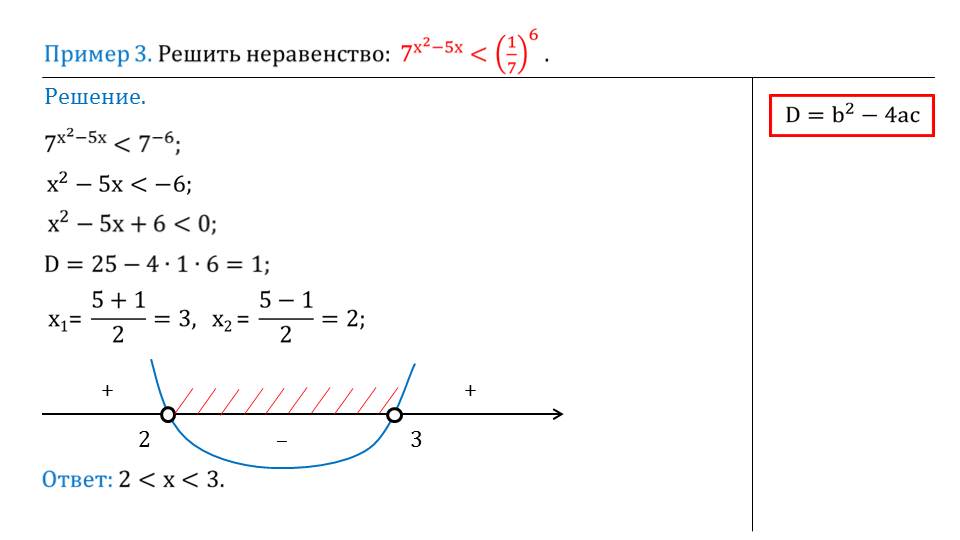
В примере 3 решается неравенство 7х2-5х<(1/7)6. Обе части неравенства приводятся к виду степеней с одинаковыми основаниями. После преобразования правой части (1/7)6=7-6 получаем неравенство7х2-5х<7-6 , которое сводится к решению неравенства х2-5х+6<0. Для этого находятся корни квадратного уравнения посредством вычисления дискриминанта. Определяются корни х1=3 и х2=2. На числовой прямой отмечаем промежуток, соответствующий требованию неравенства. Решением данного неравенства будет промежуток (2;3).
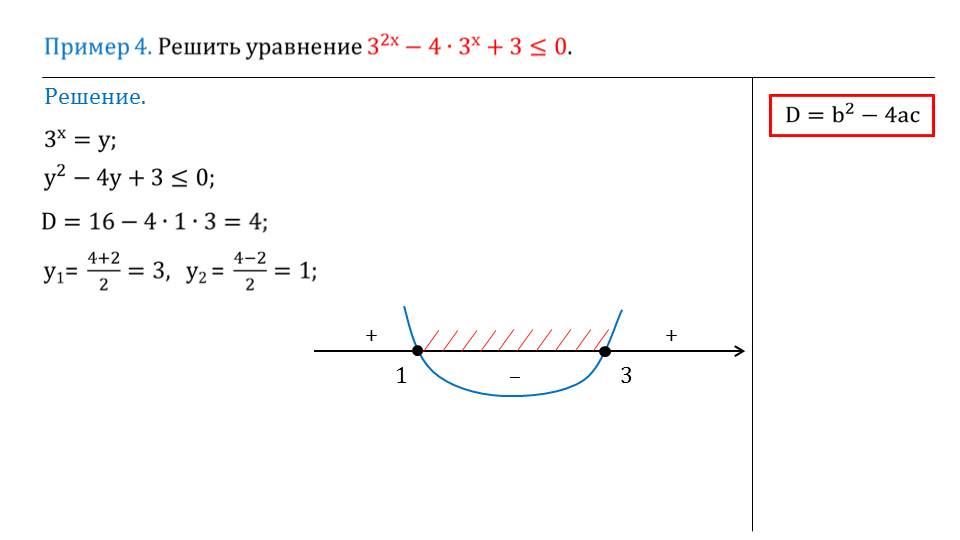
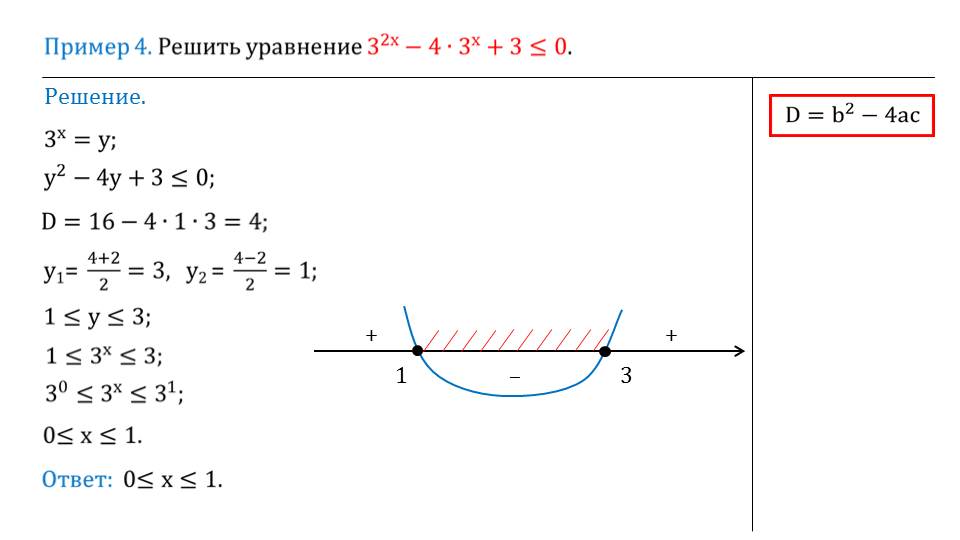
На слайде 4 описывается решение уравнения 32х-4·3х+3<=0. Чтобы решить данное неравенство, используется способ введения новой переменной. Вводится переменная у=3х. Подставив переменную, получаем новое неравенство у2-4у2+3<=0. Это обычное квадратное неравенство. Находим корни квадратного уравнения, определив дискриминант и подставив его в соответствующую формулу. Корни квадратного уравнения у2-4у2+3=0 являются значения у1=3 и у2=1. На числовой прямой отмечаем точки, соответствующие корням и штрихуем промежуток, представляющий множество решений от у=1 до у=3. Зная, что у=3х, получаем новое неравенство 30<=3х<=31. Очевидно, что решением данного неравенства будет неравенство 0<=х<=1. Это множество значений и является решением неравенства.
Презентация «Показательные неравенства» рекомендуется к использованию на уроке математики для повышения наглядности учебного материала при объяснении учителя. Также наглядность данного материала может пригодиться учителю, осуществляющему дистанционное обучение. Если ученик недостаточно хорошо усвоил тему, ему может помочь самостоятельная работа с презентацией.
| Автор | |
|---|---|
| Дата добавления | 16.11.2014 |
| Раздел | Алгебра |
| Подраздел | Презентация |
| Просмотров | 3495 |
| Номер материала | 1025 |