
Презентация "Понятие логарифма"

Краткое описание документа:
Презентация «Понятие логарифма» помогает учителю объяснить ученикам суть понятия логарифма. Пособие содержит наглядный материал для введения данного понятия, представления его определения. С помощью презентации учителю легче научить учеников вычислять логарифмы, дать необходимые знания для выполнения вычислений. В форме презентации есть возможность понятно и наглядно демонстрировать построение графиков функций, отмечать особенности построения. Выделением цвета можно облегчить запоминание понятий, свойств, особенностей решения математических задач. Применение наглядности дает возможность повысить эффективность урока, быстрее достичь учебных целей.
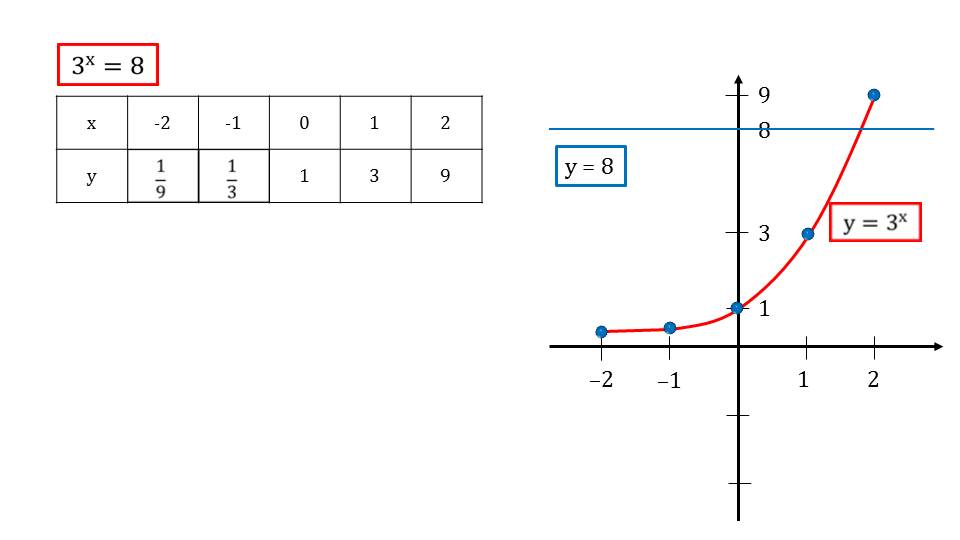

Демонстрация начинается с напоминание особенностей показательной функции. Рассматривается пример показательного уравнения 3х=8. Определяются координаты точек, принадлежащих графику этой функции. Эти координаты заносятся в таблицу. По координатам строится график функции. Также отмечается, что решением уравнения будет пересечение графиков функций у=3х и у=8.На рисунке построены данные графики.
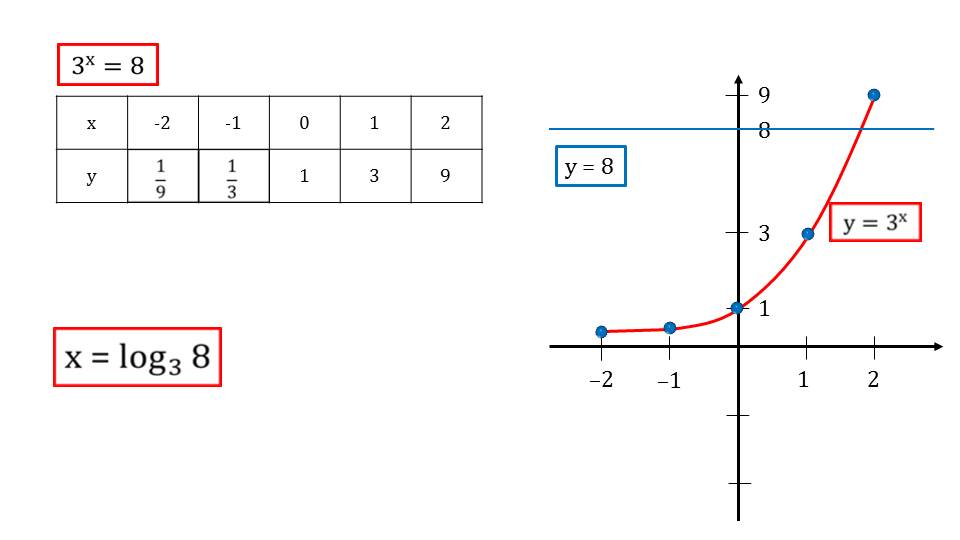

На втором слайде вводится понятие логарифма loga– логарифма по основанию а. Понятие обведено рамкой и отмечено как важное и требующее запоминания. На следующем слайде демонстрируется показательное уравнение, рассмотренное в начале презентации, и раскрывается связь между показательным уравнением 3х=8 и понятием логарифма, так как в данном уравнении х – это логарифм от 8 по основанию 3. После введения понятия и объясняющего примера ученикам представляется определение логарифма. На слайде 4 представляется определение, в котором указано, что логарифмом положительного bпо положительному основанию, не равному 1, называется показатель степени, в которую возводится а для получения числа b. Определение заключено в рамку, выделено цветом и рекомендовано для запоминания.
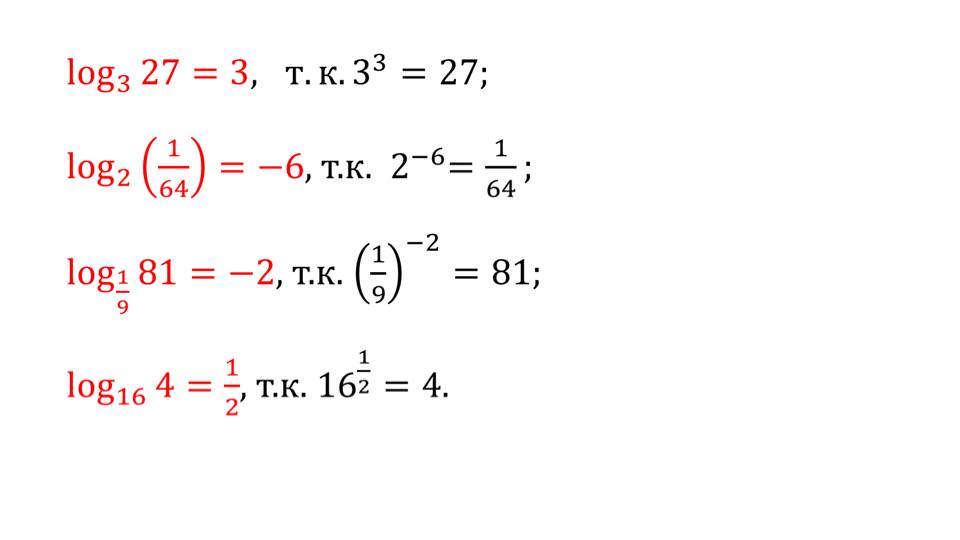

На слайде 5 рассматриваются примеры вычисления логарифмов чисел. Определяются значения логарифмов log327=3, log2(1/64)=-6, log1/981=-2, log164=1/2. Рядом с каждым примером демонстрируется, как при возведении основания логарифма в его значение получается число, от которого вычислялся логарифм. В результате такого рассмотрения сути логарифма становится понятным, как формируется значение логарифма.


На слайде 6 рассматриваются простейшие случаи вычисления логарифма, отражающие некоторые его свойства. В первом определяется логарифм logаа=1, logа1=0, logаm=m. Каждый пример проверяется возведением основания логарифма в нужную степень. На слайде 7 отмечается, что число log38 является иррациональным. Доказательство этого утверждения проверяется на слайде 8. Выполняется доказательство от противного.
Предполагается, что log38 является рациональным числом. Это значит, что решение логарифма можно представить в виде обыкновенной дроби m/n.
То есть 3m/n=8. При возведении обеих частей уравнения получаем уравнение (3m/n)n =8n. Следовательно, получаем противоречие 3m=8n. Утверждение доказано.
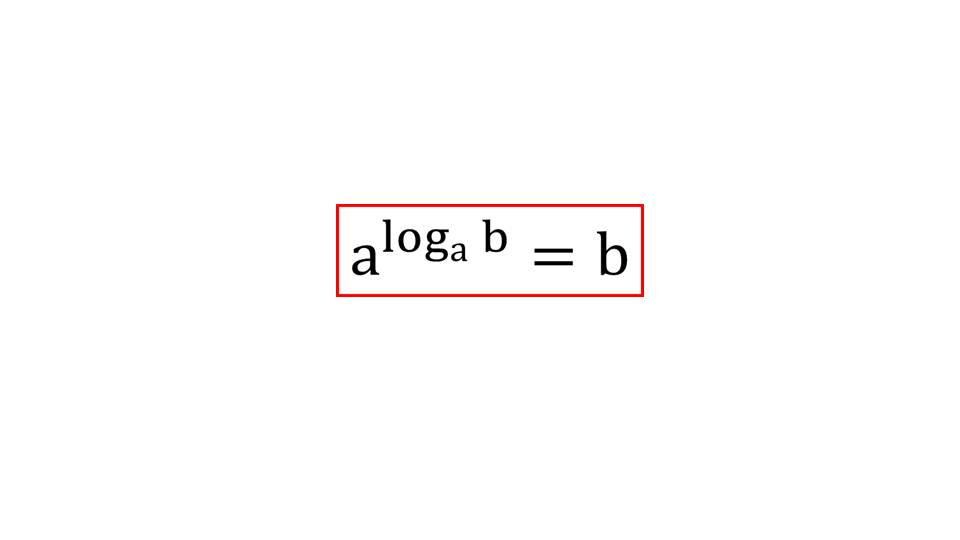
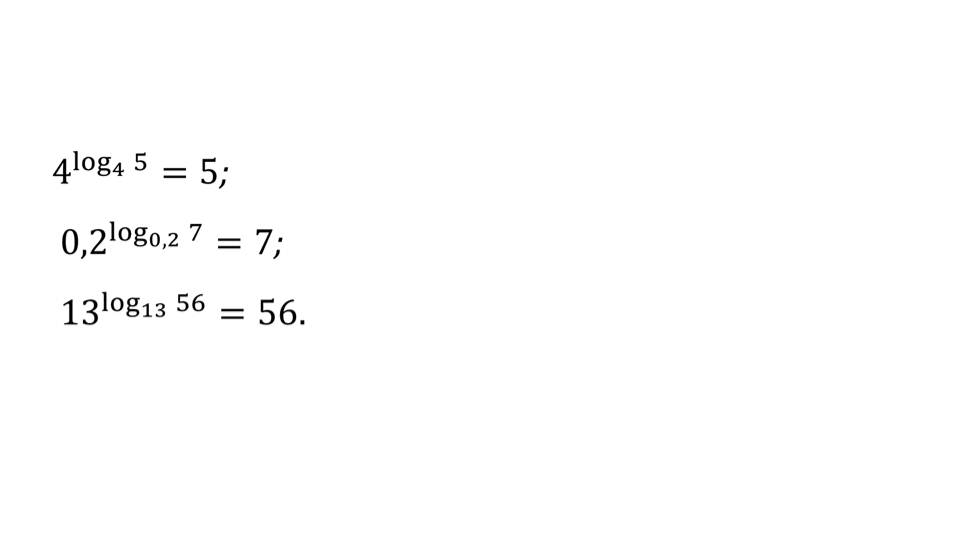
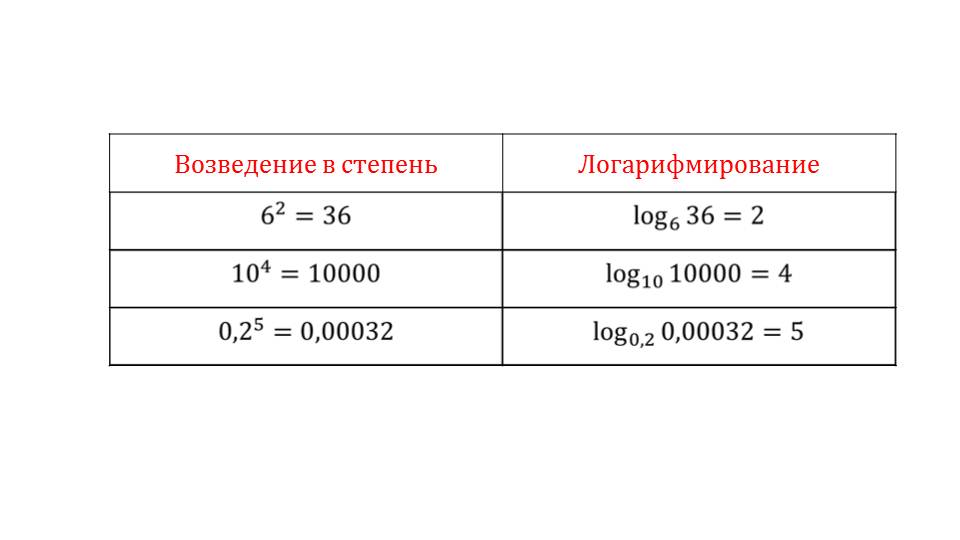
На слайде 9 представлено важное свойство логарифма а logаB=b. Для подтверждения данного правила на слайде 10 приводятся примеры 4^ log45=5, 0,2^ log0,27=7, 13^ log1356=56. Чтобы лучше понять процесс логарифмирования, представляется таблица, в левой части которой выполняется возведение в степень, а в правой части выполняется операция, обратная возведению в степень – логарифмирование. Представлены три примеры логарифмирования log636=2, log1010000=4, log0,20,00032=5.

Далее рассматривается пример вычисления выражения, в котором содержится логарифм log1/15(2253√15). Чтобы найти значение выражения, оно принимается за х. В соответствием с определением логарифма, (1/15)х=2253√15. Приводим обе части к виду, чтобы основание степени в правой и левой части уравнения были одинаковыми 15-х=152·151/3. Применив знания о свойствах степени, упрощаем выражение 15-х=152+1/3. Вычисление логарифма свелось к решению уравнения –х=7/3. Из него находим решение х=-7/3.


В примере 2 требуется вычислить значение логарифма log0,51/4√2. Аналогично предыдущему примеру, сначала применяем знание о логарифме. Вводим переменную у= log0,51/4√2. Из данного уравнения получаем (0,5)у=1/4√2. Приводим обе части уравнения к виду степени с одинаковым основанием (1/2)у=(1/2)5/2. Из данного уравнения извлекаем решение у=2,5.

Далее вводится понятие десятичного логарифма. В рамке выделено, что логарифм с основанием 10 является десятичным логарифмом и в математике обозначается log10х= lgх. На последнем слайде приводится пример записи десятичного логарифма log101000= lg1000.
Презентация «Понятие логарифма» рекомендуется для применения на школьном уроке алгебры для повышения его эффективности. Также данное наглядное пособие может быть полезно учителю, осуществляющему дистанционное обучение. Материал может быть рекомендован для самостоятельного рассмотрения учениками, которые недостаточно хорошо усвоили тему на уроке или требуют дополнительных занятий.
| Автор | |
|---|---|
| Дата добавления | 16.11.2014 |
| Раздел | Алгебра |
| Подраздел | Презентация |
| Просмотров | 4723 |
| Номер материала | 1026 |