
Презентация «Построение графика квадратичной функции»

Краткое описание документа:
Презентация «Построение графика квадратичной функции» содержит учебный материал для демонстрации учащимся при изучении данной темы. Данная презентация содержит информацию о вычислении коэффициентов для построения графика квадратичной функции на основе правил преобразования графиков, а также о порядке построения. Также в данной презентации представлены примеры, демонстрирующие, каким образом строится график функции y=ax2+bx+c.


Для пояснения особенностей применения правил преобразования графиков для построения произвольной квадратичной функции учителю необходимо структурированное понятное наглядное пособие. Презентация является наиболее удобным и эффективным способом демонстрации, так как в ней используются анимационные эффекты, важные детали и понятия выделяются цветом, подаваемый материал не требует доработки.
Презентация начинается с представления темы и квадратичной функции в виде y=ax2+bx+c. Для того чтобы построить график квадратичной функции, используя знания о преобразованиях графиков, необходимо зависимость y=ax2+bx+c привести к виду y=a(x-m)2+n. Для этого из выражения ax2+bx+c выносится общий множитель и перегруппируем слагаемые, чтобы выделить квадрат двучлена. После данных преобразований получаем выражение y=a(x+b/2a)2-(b2-4ac)/4a. Если приравнять -b/2a=m, а -(b2-4ac)/4a=n, то получим функцию, график которой строится известными преобразованиями.


Далее описывается порядок построения графика произвольной квадратичной функции. Для этого, прежде всего, необходимо уяснить, что график будет представлять собой параболу. Вершина данной параболы будет располагаться в точке , координаты которой вычисляются по формулам m=-b/2a, а n=-(b2-4ac)/4a. Также для построения графика необходимо уяснить, куда направлены ветви параболы. Ученикам напоминается, что при ветви параболы направлены вверх, а при ветви направлены вниз.
На следующем слайде представлен порядок построения квадратичной функции. Для этого предлагается прежде всего найти координаты вершины параболы, отметить ее на плоскости координат. Затем необходимо отметить несколько точек, принадлежащих данному графику и соединить их плавной линией. Для нахождения абсциссы предлагается формула m=-b/2a, а для вычисления значения функции абсцисса подставляется в формулу y=ax2+bx+c. Если находится для , то значение будет равно (так как y=ax2+bx+c=a(x-m)2+n=n)
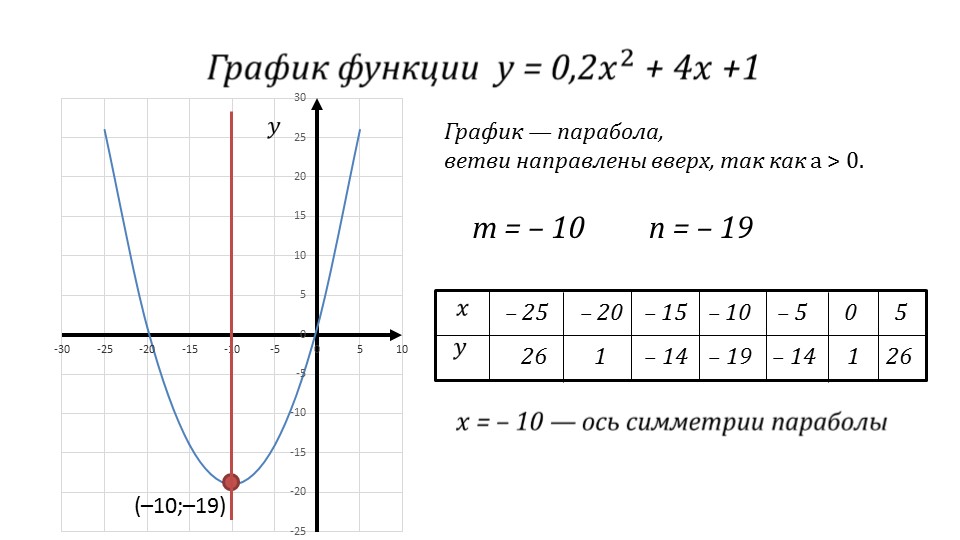
На слайде 6 предлагается согласно представленному порядку предлагается построить график функции y=0,2x2+4x+1. В начале решения задачи отмечается, что графиком служит парабола, ветви которой направлены вверх (. Подставив значения коэффициентов в формулы, получим m=-10, n=-19. Это координаты вершины параболы. Далее для построения графика необходимы координаты нескольких точек. Представим их в табличном виде, вычисляя значения нескольких точек, принадлежащих графику. Указываем, что ось симметрии параболы x=-10. Согласно данным параметрам на экране выполняется построение графика данной функции.

На слайде 7 рассматривается построение графика функции y=-3x2+12x-11. Построение производится аналогично предыдущему примеру в данном порядке. Для начала отмечается, что график функции – парабола, ветви которой направлены вниз (a=-3<0). При подстановке коэффициентов квадратного трехчлена в формулы координат вершины параболы получаем m=2, n=1. Далее находим несколько точек, принадлежащих функции, и соединим их плавной линией. Параллельно описанию процесса построения на координатной плоскости отмечаются найденные точки и демонстрируется построение графика.

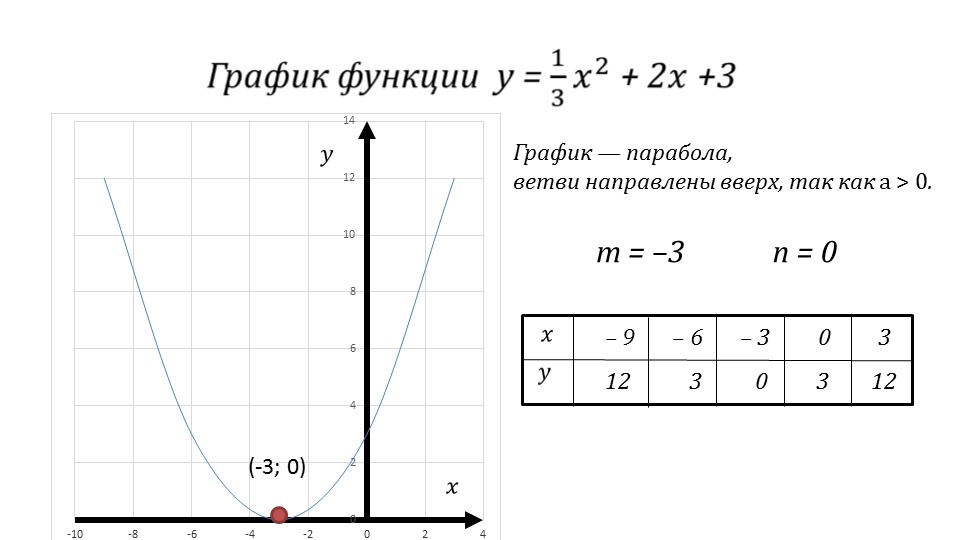
Последний слайд презентации представляет построение графика функции y=1/3 x2+2x+3. Указывается, что график данной функции – парабола, ветви которой направлены вверх, так как a=1/3>0. Для нахождения координат вершины подставляем коэффициенты квадратичной функции в выражения для нахождения координат. После вычисления получаем m=-3, n=0. Затем находим точки, принадлежащие графику данной функции, и соединяем их плавной линией. Данное построение демонстрируется рядом на рисунке.
Презентация «Построение графика квадратичной функции» помогает сформировать навыки построения графика квадратичной функции. Она может послужить наглядным пособием на уроке алгебры в школе, а также стать помощником ученика в самостоятельном освоении учебного материала. Данная презентация может быть успешно использована для дистанционного обучения.
| Автор | |
|---|---|
| Дата добавления | 29.08.2014 |
| Раздел | Алгебра |
| Подраздел | Презентация |
| Просмотров | 4854 |
| Номер материала | 645 |