
Презентация "Предел числовой последовательности. Определение предела последовательности"

Краткое описание документа:
Презентация «Предел числовой последовательности. Определение предела последовательности» является наглядным пособием для представления учебного материала по данной теме. Пособие предназначено для формирования представления учеников о пределе числовой последовательности. Материал может использоваться на этапе объяснения учителем новой темы. Также в презентации разбирается решение примеров, в которых необходимо вычислить предел последовательности для усвоения материала.
В презентации используются приемы, улучшающие подачу учебной информации для усвоения и запоминания. Анимационные эффекты удерживают внимание учеников. С их помощью материал подается последовательно и логично. Важные определения выделяются рамкой и окрашиванием в яркий цвет, способствуя запоминанию. Наглядность материала дает возможность повысить эффективность обучения, углубляя понимание предмета изучения.


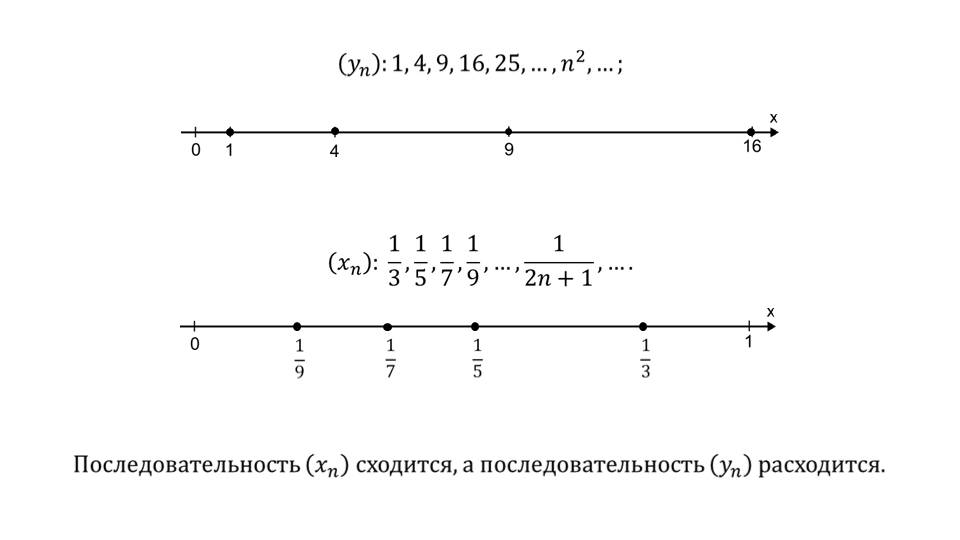
Презентация начинается со сравнением поведения на числовой оси последовательностей (yn)1, 4, 9, 16,…, n2,… и (xn) 1/3, 1/5, 1/7, …, 1/(2n+1),… На числовой оси, рисунок которой сопровождает каждый пример, отмечаются числа, соответствующие значению членов последовательности. При этом видно, что расстояние между членами первой последовательности растет, а расстояние между членами второой последовательности при возрастании порядкового номера уменьшается. Внизу слайда отмечается, что первая последовательность расходится, а вторая сходится.
Для получения представления о пределе последовательности необходимо усвоить понятие окрестности точки.


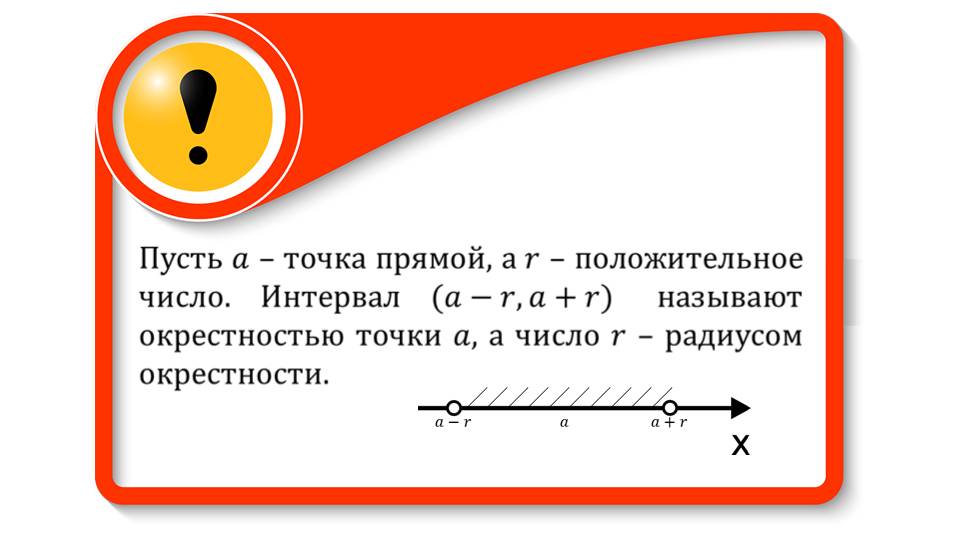
На слайде 2 дано определение окрестности точки, которая представляет собой интервал (a-r, a+r) для точки а, где r-радиус окрестности. На числовой прямой отмечена данная точка, заштрихована область с радиусом r около нее. Примером окрестности служит данный на слайде 3 интервал (6,97; 7,03), который представляет окрестность точки 7 с радиусом 0,03. Здесь же дано представление предела последовательности как точки сгущения.
После освоения рассмотренных понятий, ученикам дается определение предела последовательности (yn) как некоторого числа b, в некоторой окрестности которого, начиная с некоторого члена последовательности, содержатся все оставшиеся члены. Вводится обозначение предела yn→0 или limyn=b.


На слайде 5 указаны комментарии к понятию предела последовательности, которые помогают ученику понять суть данного определения. Оно означает, что если существует некоторый предел последовательности limyn=bпри стремлении порядкового номера ее членов к бесконечности, то для некоторого интервала (b-r1, b+r1), r1>0 существует порядковый номер члена, начиная с которого все остальные члены последовательности располагаются в указанной окрестности, то есть некоторый yn1, yn+1, и т.д принадлежат этой окрестности.


Также на слайде 6 пояснения переносятся на окрестность с еще меньшим радиусом. Замечено, что условие содержания в окрестности всех членов последовательности, начиная с некоторого номера, сохраняется, но порядковый номер начального члена увеличивается. К пояснениям также добавляется замечание, что для b - предела последовательности (yn) окрестность, куда попадают члены, начиная с yn0, можно представить отрезком, в который попадают все последующие члены. При уменьшении размеров окрестности (отрезка), вне его пределов остается больше членов последовательности. При этом, начиная с некоторого порядкового номера, оставшиеся члены все равно попадают в данную окрестность.

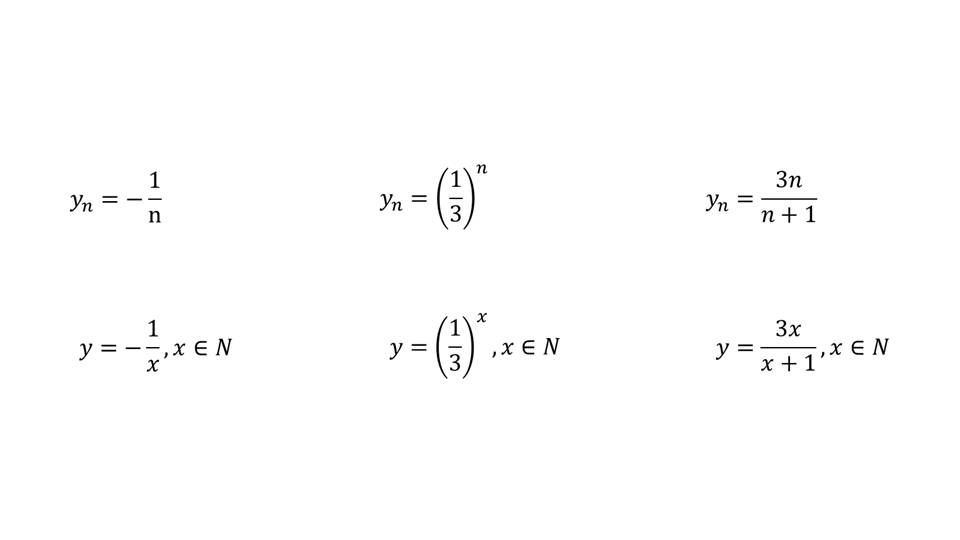
Для усвоения представленного материала предлагается рассмотреть решение примера. В нем необходимо доказать, что предел, к которому стремиться последовательность (xn) -1, -1/2, -1/3,…,-1/n,…, равен нулю. Для доказательства утверждения на рисунке строится числовая прямая, на которой отмечается точка 0 и заштриховывается окрестность вокруг нее с радиусом r. Замечено, что можно подобрать некоторый порядковый номер n0, что -1/n0>-r. Например, для r=0,0001 n=10001, так как для них выполняется неравенство и т.д. Поэтому в соответствии с определением предел последовательности lim(-1/n) =0 при n→∞.
В примере 2 необходимо найти предел последовательности 1/3, 1/9, 1/27, 1/81,…,(1/3)n,… анализируя аналогично случаю в предыдущем примере, можно доказать, что данная последовательность стремится к нулю, то есть lim(1/3)n =0 при n→∞. Отмечается, что полученные результаты представляют собой частный случай общего утверждения, представленного на следующем слайде.
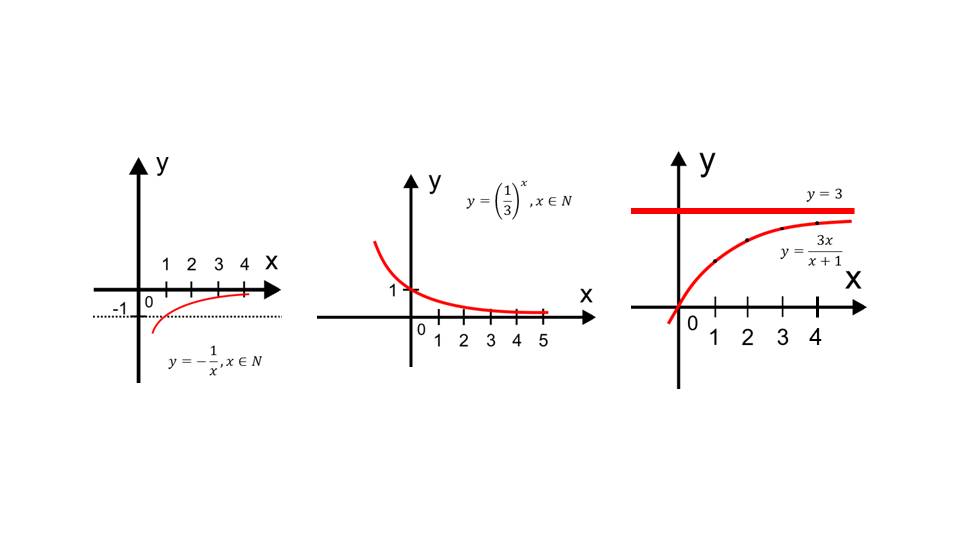
На слайде 10 дается общее представление определения предела для последовательности с |q|<1, где lim(q)n =0 при n→∞. При |q|>1 последовательность будет расходиться.Примером служит последовательность, где q=5. При увеличении порядкового номера членов последовательности, очевидно, значения членов растут, стремясь к бесконечности.
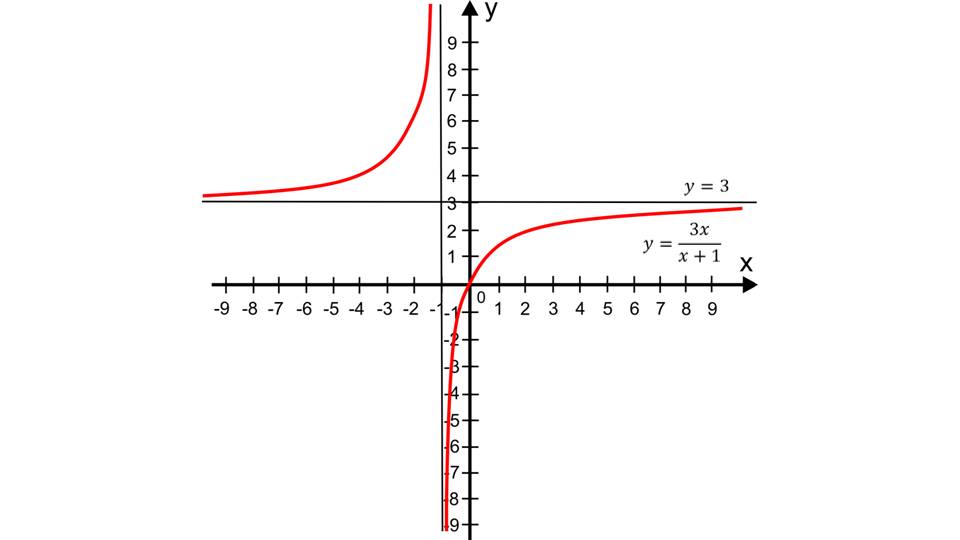
На слайде 11 рассматривается поиск предела последовательности 3/2, 6/3, 9/4,…,3n/(n+1). Чтобы получить наглядное поведение последовательности, выражение преобразуется к равнозначному виду 3-3/(n+1). Ри подстановке порядковых номеров видно, что из числа 3 вычитается все меньшее число, постепенно приближая члены последовательности к значению 3. Поэтому lim3n/(n+1)=3 при n→∞.
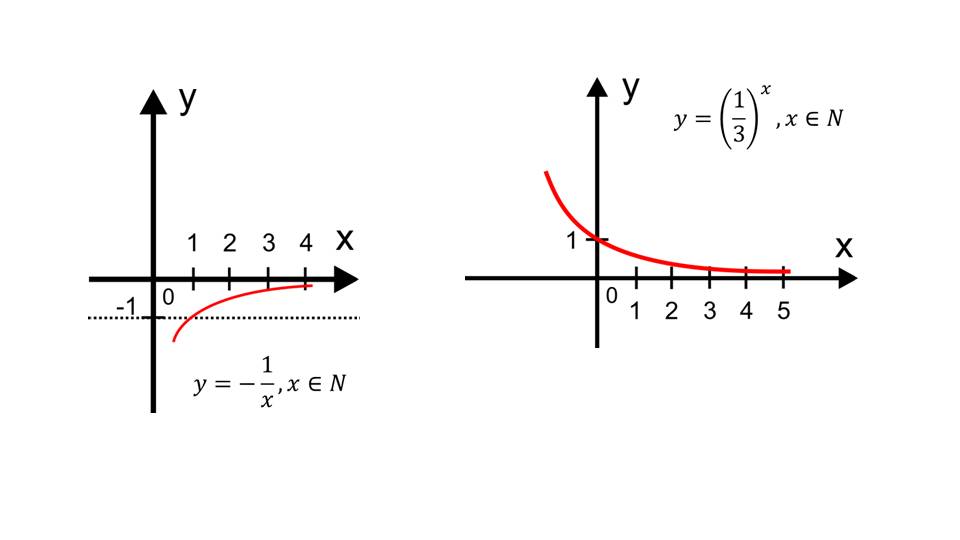
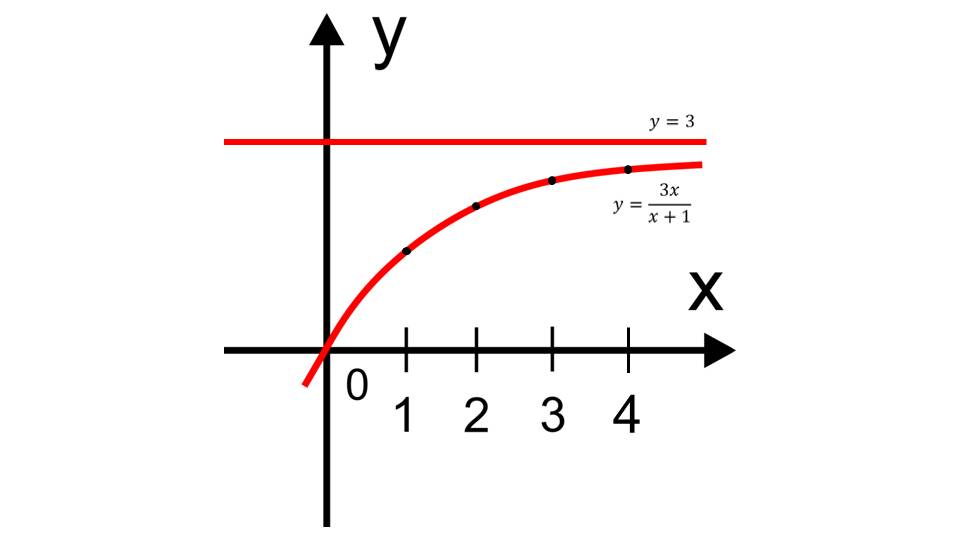
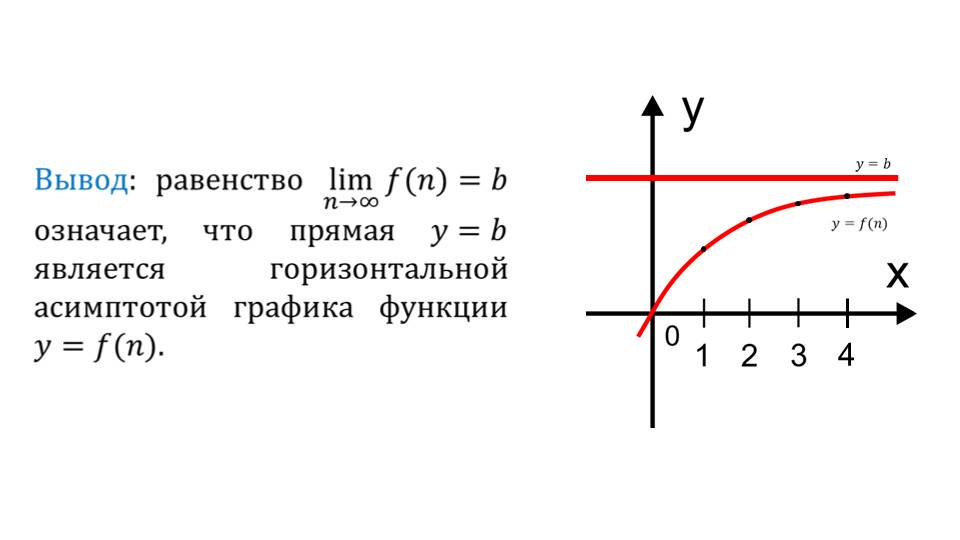
На слайде 12 представлены последовательности, поведение которых необходимо проанализировать: yn=-1/n, yn=(1/3)n, yn=3n/(n+1). Аналитическое задание данных последовательностей выглядит в виде зависимостей y=-1/x, y=(1/3)x, y=3x/(x+1) для всех натуральных x. На слайдах 13-17 представлены графики данных функций, на которых видно, что если последовательность стремится к некоторому пределу, то на графике функции это определяется стремлением графика к горизонтальной асимптоте. Соответствующий вывод отображен на последнем слайде презентации.
Презентация «Предел числовой последовательности. Определение предела последовательности» рекомендуется использовать на традиционном уроке алгебры как наглядное пособие, сопровождающее объяснение учителем новой темы. Пособие может быть использовано в качестве инструмента обучения в ходе дистанционного обучения. При необходимости углубить понимание темы материал может быть рекомендован ученикам для самостоятельной работы.
| Автор | |
|---|---|
| Дата добавления | 27.07.2014 |
| Раздел | Алгебра |
| Подраздел | Презентация |
| Просмотров | 6971 |
| Номер материала | 815 |