
Презентация "Предел функции"

Краткое описание документа:
Презентация «Предел функции» - наглядное пособие, помогающее в изучении материала по данной теме по алгебре. Пособие содержит подробное понятное описание теоретического материала, раскрывающего понятие предела функции, его графического представления, правил вычисления предела функции, связи свойств функции с ее пределом. Все теоретические основы, изложенные в презентации, по ходу демонстрации подкрепляются описанием решения соответствующих заданий.

Представление материала в форме презентации дает возможность подать изучаемые понятия более удобно для понимания. Использовать эффективные инструменты для запоминания материала.
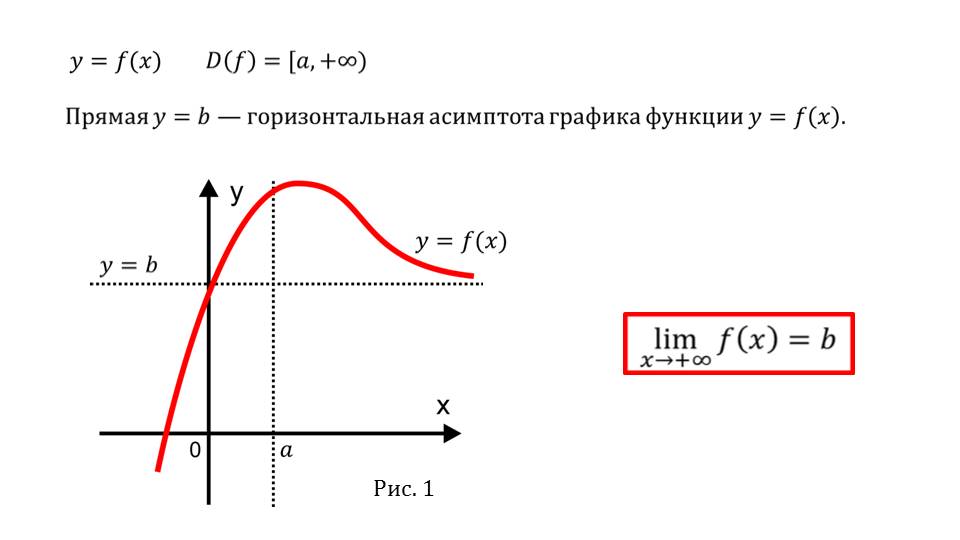
Презентация начинается с напоминания вида функциональной зависимости y=f(n), nϵN. Раскрывается смысл предела функции при построении графика этой функции. Отмечается, что равенство limf(n)=bпри n→∞ означает, что прямая у=b, проведенная на координатной плоскости, представляет собой горизонтальную асимптоту, к которой стремится график функции при n→∞. На втором слайде на координатной плоскости изображен график функции y=f(х), область определения которого лежит на промежутке D(f)=[a, +∞).


На рисунке также построена горизонтальная асимптота у=b. Отмечается, что при стремлении х→+∞ в области определения функции, ее значения приближаются к асимптоте, следовательно limf(х)=b при х→+∞. Аналогично рассмотренному приближению значений функции к пределу при стремлении к +∞, описывается ее поведение при стремлении к -∞.

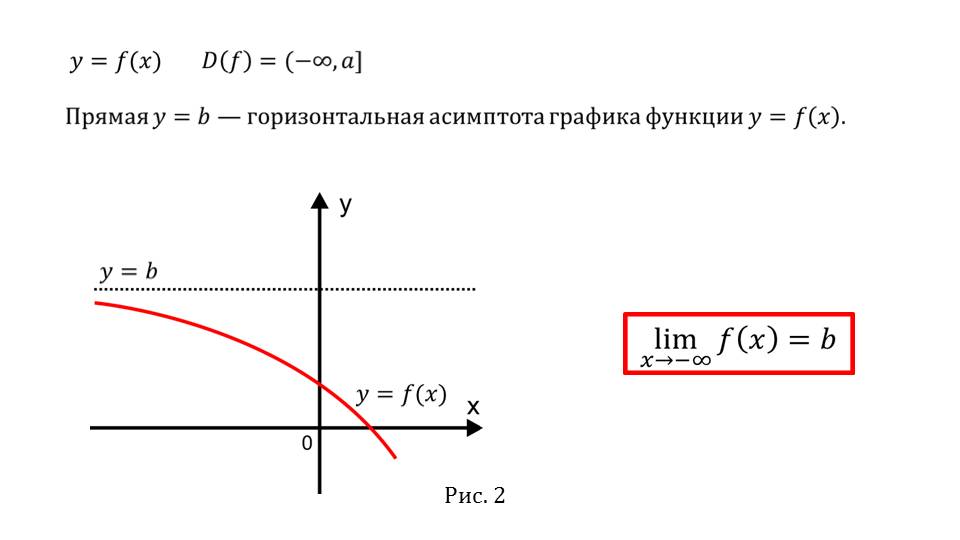
На слайде 3 представлена некоторая функция y=f(х). область определения которой лежит по левую сторону от точки а, то есть D(f)=( +∞, a]. При наличии горизонтальной асимптоты у=b в области определения функция стремится к значению предела limf(х)=b при х→-∞. Приближение функции к асимптоте продемонстрировано на соответствующем рисунке, представленном на слайде.


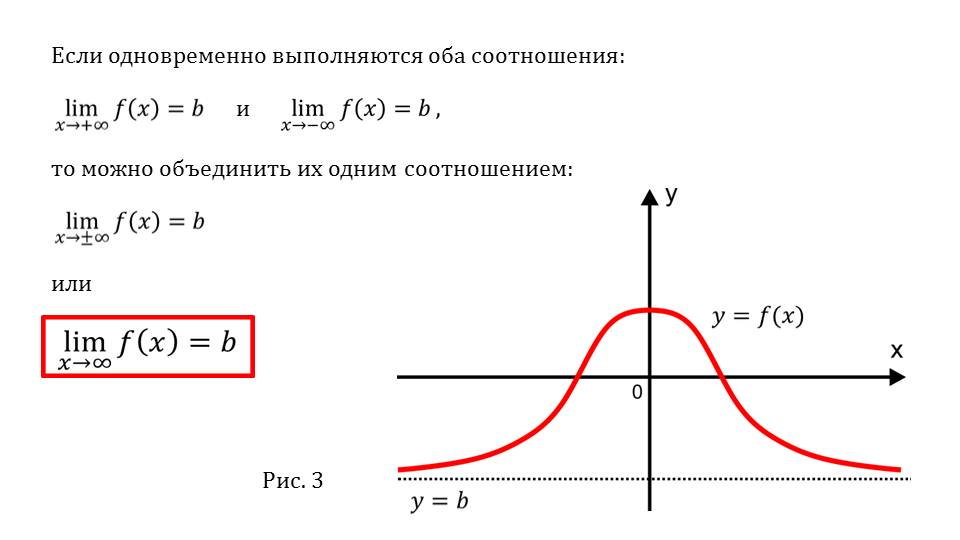
На слайде 4 описывается случай приближения графика функции к горизонтальной асимптоте при стремлении ее аргумента и к +∞, и к -∞. Это означает одновременное выполнение условий limf(х)=b при х→-∞ и limf(х)=b при х→+∞. Иначе можно записать limf(х)=b при х→∞. На рисунке продемонстрирован пример такой функции и поведения ее графика на координатной плоскости.


Далее демонстрируются правила вычисления предела функции. В свойстве 1 отмечается, что для функции k/xm при натуральном m верно будет равенство lim(k/xm)=0 при х→∞. Во втором пункте указывается, что для пределов двух функций limf(х)=b и limg(х)=cбудут справедливы аналогичные свойства пределов последовательностей. То есть предел суммы определяется суммой пределов lim(f(х) + g(х))= b+с, предел произведения равен произведению пределов limf(х) g(х)= bс, предел частного равен частному пределовlimf(х)/g(х)= b/с при g(х)≠0 и с≠0, а также постоянный множитель может выносится за знак предела limkf(х) = kb.


Закрепить полученные знания можно при помощи описания решения примера 1, в котором нужно определить lim(√3·х5-17)/(х5+9). Для получения решения числитель и знаменатель дроби делятся на высшую степень переменной, то есть х5. После вычисления получаем lim(√3-17/ х5)/(1+9/х5).


Оценив пределы и воспользовавшись свойством предела частного, определяем, что lim(√3·х5-17)/(х5+9)=√3/1=√3. К данному примеру дается важное замечание, что вычисление пределов функции аналогично вычислению пределов последовательностей, но в данном случае нужно учесть, что х не может принимать значение -5√9, которое обращает знаменатель в нуль.

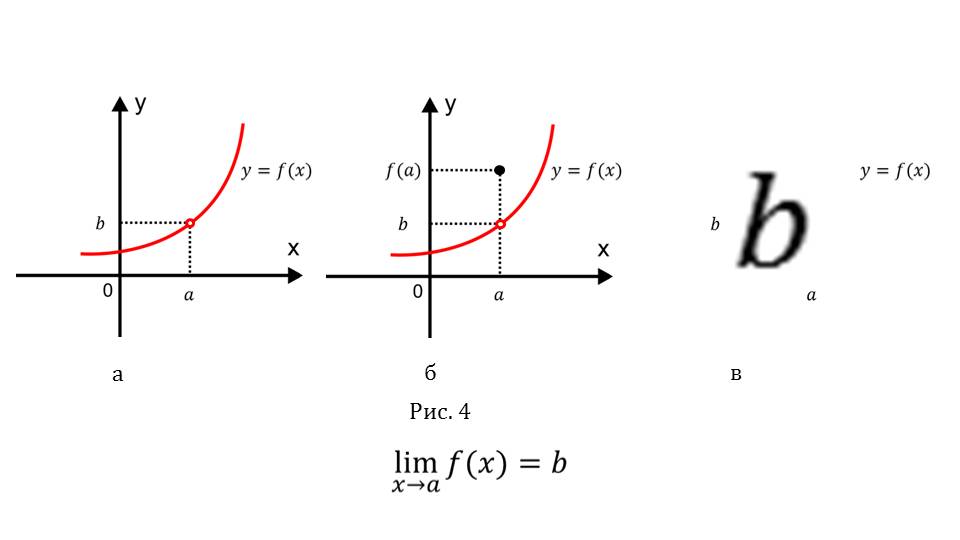
На следующем слайде рассмотрен случай, когда х→a. На рисунке хорошо видно, что для некоторой функции f(х) при приближении переменной к точке а, значение функции приближается к ординате соответствующей точки на графике, то есть limf(х)=b при х→a.


Слайды 9, 10, 11 содержат определения, раскрывающие понятия непрерывности функции, непрерывной функции в точке, на промежутке. При этом непрерывной считают функцию, у которой limf(х)= f(а) при х→a. В точке а функция будет непрерывной, если верно соотношение limf(х)= f(а) при х→a, а непрерывной на промежутке Х будет функция, непрерывная в любой точке промежутка Х.
Приводятся примеры оценки непрерывности функций. Отмечено, что функции у=С, y=kx+m, y=ax2+bx+c, y=|x|, y=xn для натуральных n являются непрерывными на всей числовой прямой, функция у=√х непрерывна на положительной полуоси, а функция y=xn непрерывна на положительной полуоси и отрицательной полуоси с разрывом в точке 0, непрерывными будут тригонометрические функции у=sinx, у=cosxна всей прямой, а у=tgx, у=ctgxпо всей области определения. Также функция, состоящая из рациональных или иррациональных, тригонометрических выражений, она является непрерывной для всех точек, где определена функция.


В примере 2 нужно вычислить предел lim (x3+3x2-11х-8) при х→-1. В начале решения отмечается, что данная функция, состоящая из рациональных выражений, определена на всей числовой оси и в точке х=-1. Поэтому функция является непрерывной в точке х=-1 и при стремлении к ней предел получает значение функции, то есть lim (x3+3x2-11х-8)=5 при х→-1.
Пример 3 демонстрирует вычисление предела lim (cosπx/√x+6) при х→1. Отмечается, что функция определена на всей числовой оси, поэтому является непрерывной и в точке х=1, следовательно, lim (cosπx/√x+6)=-1/7 при х→1.
В примере 4 требуется вычислить lim((x2-25)/(x-5)) при х→5. Данный пример особенный тем, что для х=5 знаменатель функции обращается в нуль, что недопустимо. Определить предел можно, преобразовав выражение. После сокращения получаем f(х)=х+5. Только в поиске решений следует учесть, то х≠5. При этомlim((x2-25)/(x-5))= lim(x+5)=10 при х→5.
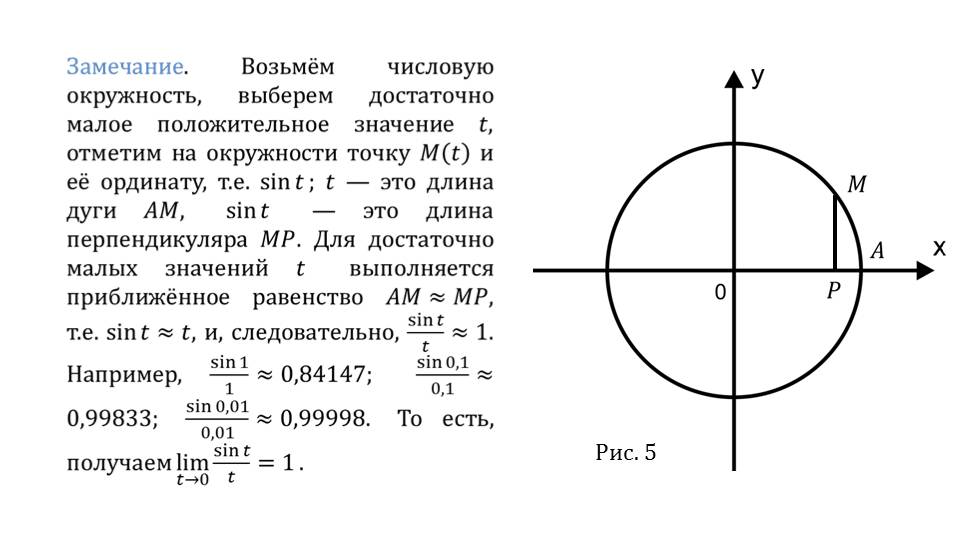
На слайде 17 описано замечание, которое демонстрирует получение важного предела lim(sint/t)=1 при t →0, используя числовую окружность.
Слайд 18 представляет определение приращения аргумента и приращения функции. Приращение аргумента представлено разностью переменных х1-х0 для функции, определенной в точках х0 и х1. При этом изменение значения функции f(х1)- f(х0) называется приращением функции. Вводятся обозначения приращения аргумента Δх и приращения функции Δ f(х).
В примере 5 определяется приращение функции y=x2 при переходе точки х0=2 к х=2,1 и х=1,98. Решение примера сводится к поиску значений в исходной и конечной точках и их разности. Так, в первом случае Δу=4,41-4=0,41, а во втором случае Δу=3,9204-4=-0,0796.
На слайде 21 отмечается, что при х→а справедлива запись (х-а)→0, что означает Δх→0. Также при стремлении f(х) → f(а), используемом в определении непрерывности справедлива запись f(х)-f(а) →0, то есть Δу→0. Используя данную запись, дается новое определение непрерывности в точке х=а, если для функции f(х) справедливо условие: если Δх→0, то Δу→0.


Для закрепления материала описывается решение примеров 6 и 7 ,в которых нужно найти приращение функции и предел отношения приращения функции к приращению аргумента. В примере 6 это нужно сделать для функции y=kx+m. Выводится приращение функции при переходе точки из х в (х+ Δх), демонстрируя изменения на графике. При этом получается Δу= kΔх, а lim(Δу/ Δх)=k при Δх→0. Аналогично разбирается поведение функции у=х3. Приращение данной функции при переходе точки из х в (х+ Δх) равно Δу=(3х2+3х Δх+( Δх)2) Δх, а предел функции lim(Δу/ Δх)=3х2.
Презентация «Предел функции» может использоваться для ведения традиционного урока. Презентацию рекомендуется применять как инструмент дистанционного обучения. При необходимости самостоятельного изучения темы учеником пособие рекомендуется для самостоятельной работы.
| Автор | |
|---|---|
| Дата добавления | 27.07.2014 |
| Раздел | Алгебра |
| Подраздел | Презентация |
| Просмотров | 13624 |
| Номер материала | 817 |