
Презентация "Преобразование произведений тригонометрических функций в суммы"

Краткое описание документа:
Презентация «Преобразование произведений тригонометрических функций в суммы» представляет наглядный материал для проведения урока геометрии по данной теме. В ходе демонстрации ученикам представляются формулы преобразования произведения косинусов в суммы тригонометрических функций и преобразования синусов в в суммы тригонометрических функций. С целью усвоения материала описано подробное решение четырех примеров, для решения которых требуется знание изученных формул. Задача презентации – обеспечить наглядное представление материала, способствовать запоминанию формул, формировать умение решать задания с использованием изученных формул.
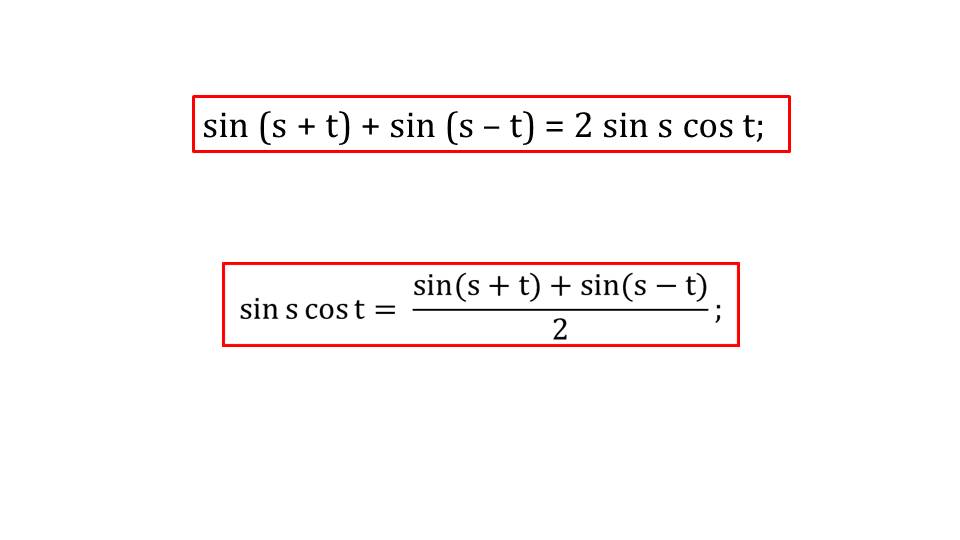
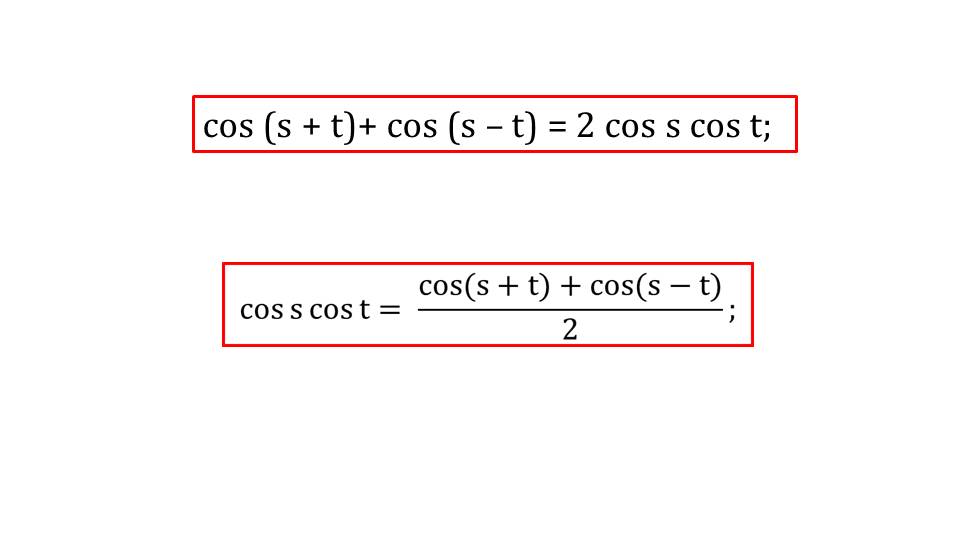
Наглядное пособие в форме презентации имеет много преимуществ, которые помогают повысить эффективность урока. Анимационные эффекты помогают удержать внимание учащихся на изучаемом предмете. Также при помощи анимации упорядочена подача информации, лучше видна последовательность действий при решении задач. В презентации есть возможность выделения понятий и формул для лучшего их запоминания, акцентирования внимания на важных деталях.
Презентация начинается с представления формулы преобразования произведения синуса некоторого аргумента на косинус другого аргумента sin s cos t=(sin(s+t)+sin(s-t))/2. На экране продемонстрировано, как такую формулу легко получить, используя изученную ранее формулу суммы синусов sin(s+t)+sin(s-t)= 2sin s cos t. Она получается делением обеих частей равенства на 2.
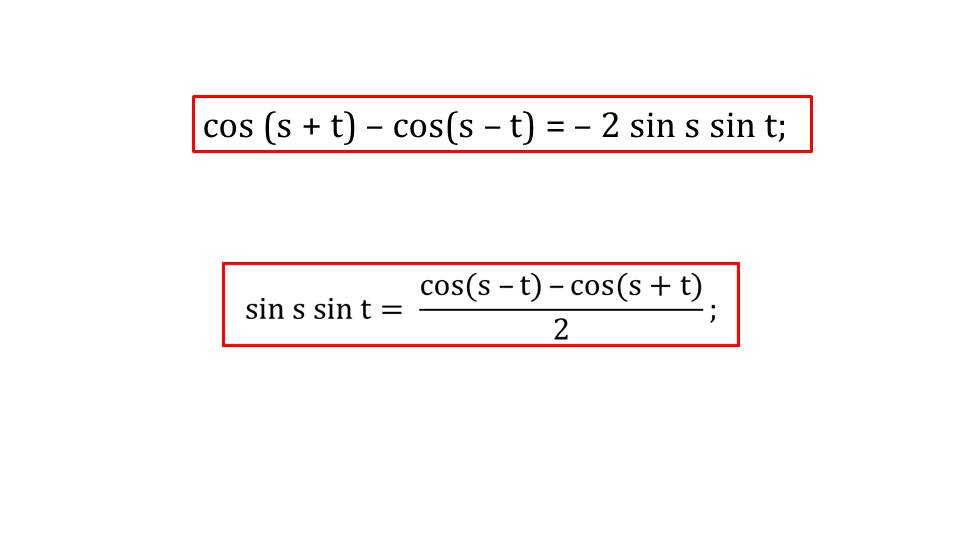

На втором слайде представлена формула преобразования произведения косинусов в сумму. Основой для получения такой формулы послужила формула суммы косинусов, вид которой напоминается ученикам на этом же слайде. После деления обеих частей равенства на 2 в данной формуле получается искомая формула вида 2 cos s cos t = (cos(s+t) - cos(s-t))/2, представленная на экране и выделенная в рамку.
Далее рассматривается решение примеров, для поиска решений которых необходимо применять изученные формулы. На слайде 4 описывается решение задания, в котором нужно преобразовать произведение sin 2х cos 9х в сумму. Для решения данного примера нужно вспомнить изученную формулу преобразования произведения синуса на косинус. Применив данную формулу, получаем выражение, представляющее собой сумму тригонометрических функций. После приведения подобных слагаемых вы решении получаем формулу вида (sin 11х - sin 7х)/2.

В примере 2 требуется преобразовать произведение cos (2х-у) cos (х+4у) в сумму. Ученикам напоминается формула преобразования произведения косинусов, изученная в ходе видеоурока. Задание решается прямым применением данной формулы, подставив вместо переменных s=(2x-y), t=(x+4y). Применив данную формулу, получаем дробь, которая после выполнения вычислений в числителе принимает вид (cos (3х+3у) + cos (х-5у))/2. Данная дробь и является решением задания.

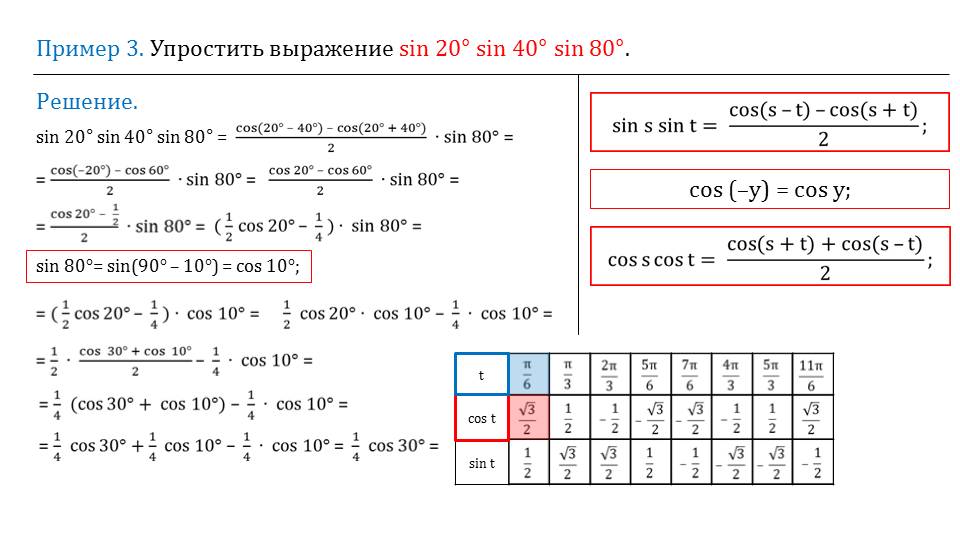
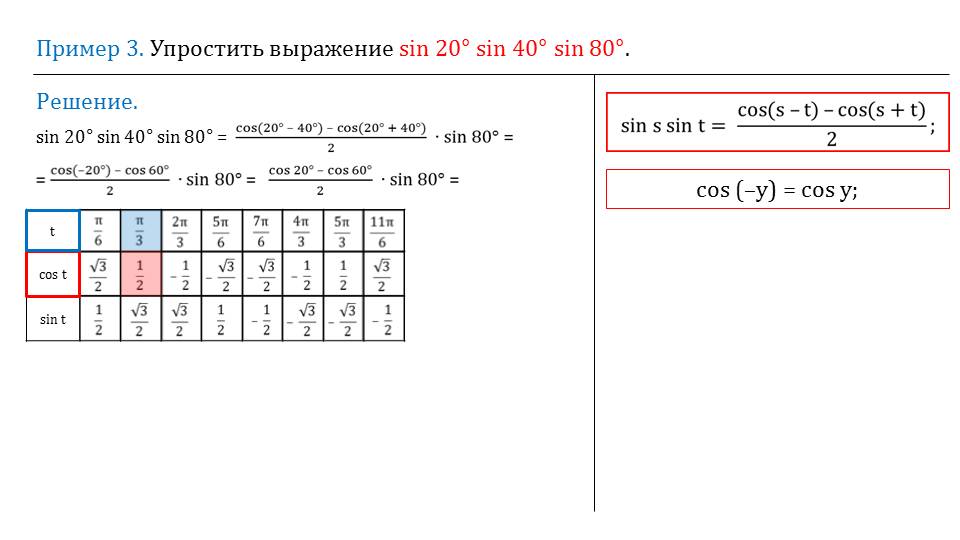
Пример 3 описывает упрощение выражения sin 20°sin 40°sin 80° с использованием формулы произведения синусов. Данная формула отображена в правой части слайда для напоминания ее вида ученикам. Также справа выведено свойство четности функции косинуса. Для преобразования произведения первых двух синусов применяется изученная формула. После этого выражение получает вид ((cos(20°-40°) - cos(20°+40°))/2)*sin 80°. После простых вычислений в данном выражении и использования свойство четности косинуса получаем вид (cos 20° - cos 60°)*sin 80°. На экран выводится таблица распространенных значений тригонометрических функций, из которой можно выбрать подходящее значение для cos 60° и подставить его в выражение. Вспомнив соответствующую формулу приведения, отмечается, что sin 80° можно преобразовать sin 80°= sin (90°-10°)=cos 10°. После подстановки данного значения и после раскрытия скобок получаем выражение, в котором есть произведение косинусов. Для его преобразования применяем изученную формулу. Применив формулу и проведя возможное сокращение, получаем выражение ¼ cos 30°. Значение cos 30° можно выбрать из таблицы значений тригонометрических функций, после подстановки которого получаем решение sin 20°sin 40°sin 80°=√3/2.
В последнем примере требуется решить уравнение 2 sin 2x cos 9x – sin 11x=0. Очевидно, при решении данного задания понадобится изученная на уроке формула преобразования произведения синуса на косинус. Вместо аргументов в формулу подставляем аргументы из задания s=2x; t=9x. После применения формулы, произведение принимает вид 2 sin 2x cos 9x = 2·( sin 11x - sin 7x)/2. Сократив общие множители в числителе и знаменателе и приведя подобные, получаем значение выражения sin 11x - sin 7x. После подстановки выражение в уравнение части sin 11x сокращаются, и уравнение принимает вид - sin 7x=0 Решением такого уравнения является x= πn/7 для любого целого n. Решение найдено.


Презентация «Преобразование произведений тригонометрических функций в суммы» применяется для наглядности объяснения учителя по данной теме на традиционном уроке в школе. Также материал может применяться в ходе дистанционного обучения. Пособие может быть рекомендовано ученикам, которым требуется дополнительный материал для более глубокого освоения предмета изучения.
| Автор | |
|---|---|
| Дата добавления | 27.07.2014 |
| Раздел | Алгебра |
| Подраздел | Презентация |
| Просмотров | 8179 |
| Номер материала | 812 |