
Презентация "Преобразование сумм тригонометрических функций в произведения"

Краткое описание документа:
Презентация «Преобразование сумм тригонометрических функций в произведения» наглядно представляет учебный материал по данной теме. В ходе демонстрации описывается выведение формул преобразования суммы синусов и косинусов в произведения, приводятся примеры использования формул для решения задач. Наглядное пособие может сопровождать объяснение новой темы и этап усвоения материала на традиционном уроке алгебры. Задача презентации – наглядно представить образование формул для преобразования тригонометрических функций в произведения, формировать умения решать задания с использованием формул.


Для выведения формулы преобразования суммы синусов в правой части первого слайда отображается формула синуса разности и суммы аргументов. В основной части слайда представлена сумма синусов sin(s+t)+sin(s-t). Используя формулы, представленные справа, оба синуса представляются в виде суммы произведений. После открытия скобок и приведения подобных слагаемых в результате вычислений остается выражение 2sin s cos t.
Если принять выражения, представленные в скобках синуса, за некоторые переменные x=s+t, y=s-t., то их сумма x+y=2s. Из нее можно вывести s=(x+y)/2. Для выражения через введенные переменные переменной t находим разность x-y=s+t-(s-t). После раскрытия скобок и приведения подобных слагаемых определяем формулу для определения переменной t=(x-y)/2. С учетом выведенных для переменных формул получаем выражение для определения суммы синусов sin x + sin y = 2 sin (x+y)/2 cos (x-y)/2.


На слайде 5 описывается пример применения формулы для преобразования суммы синусов в произведение. После подстановке выражения согласно формуле получаем преобразование sin 7x + sin 3x = 2 sin 5x cos 2x.
Далее описывается выведение формулы преобразования суммы синусов в произведение. Для этого в правую часть экрана выводятся изученные формулы, которые необходимы для получения выражения. Это формула суммы синусов sin x + sin y = 2 sin (x+y)/2 cos (x-y)/2 и свойство синуса от отрицательного аргумента –sin y=sin (-y). Для выведения формулы преобразования разности синусов разность представляется в виде суммы синусов, один из которых взят от отрицательного аргумента. Применив формулу преобразования суммы синусов, получаем выражение вида sin x - sin y = 2 sin (x+(-y))/2 cos (x-(-y))/2. После раскрытия скобок отрицательного значения получаем формулу преобразования разности синусов в произведение sin x - sin y = 2 sin (x-y)/2 cos (x+y)/2.
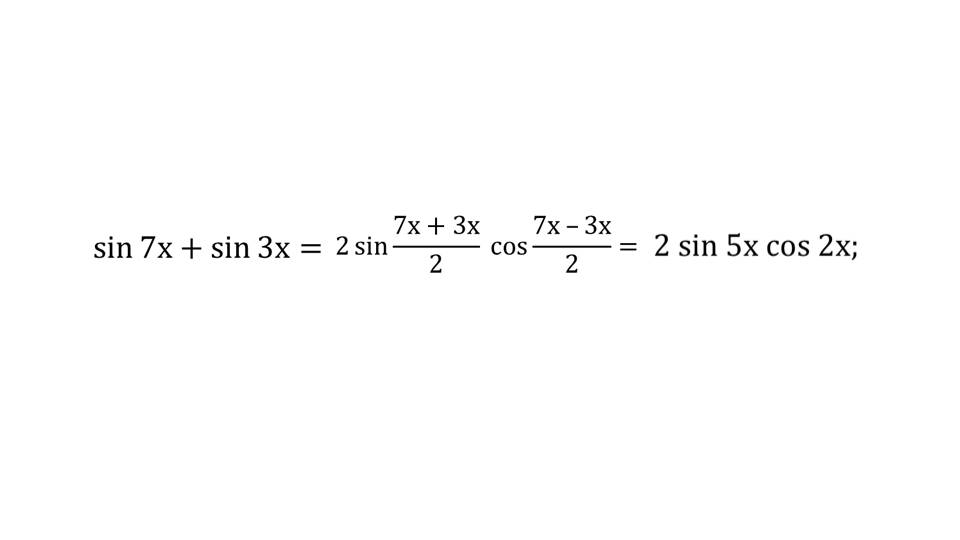

На слайде 7 описывается пример применения выведенной формулы для решения задания. В задании необходимо упростить выражение sin 77° - sin 17°. Задание решается прямым использованием формулы с подстановкой соответствующих аргументов. После подстановки аргументов получаем выражение 2 sin (77°-17°)/2 cos (77°+17°)/2, которое после вычисления значений получает вид 2 sin 30° cos 47°. Зная, что sin 30°=1/2, при подстановке значения в выражение, решение сводится к вычислению cos 47°, то есть sin 77° - sin 17°= cos 47°.


На слайде 8 выводится формула преобразования суммы косинусов. Для этого в правой части слайда отображаются формулы, которые необходимо вспомнить для проведения необходимых преобразований. Это формулы косинуса суммы и разности cos (x+y)= cos x cos y-sin x sin y и cos (x-y)= cos x cos y+sin x sin y. Для выведения формулы суммы косинусов аргумент представлен в виде суммы и разности переменных s и t, то есть cos(s+t) + cos(s-t). После применения формулы преобразования косинуса суммы и разности, получаем выражение cos s cos t+sin s sin t + cos s cos t+sin s sin t. После приведения подобных слагаемых получаем cos(s+t) + cos(s-t)= 2cos s cos t. Вводим новые переменные х и у, которые можно представить через s и t. Поэтому s=(х+у)/2, а t=(х-у)/2. После подстановки введенных переменных получаем формулу преобразования суммы косинусов cos x+cos y=2 cos (x+y)/2 cos (x-y)/2.
На слайде 9 описывается пример, в котором упрощается выражение cos(x+2y) + cos(3x-2y). В решении данного задания потребуется знать свойство косинуса от отрицательного аргумента cos(-t)=cos t, которая отображается в правой части слайда. Задание решается прямым применением формула преобразования суммы косинусов. После раскрытия скобок и приведения подобных слагаемых получаем произведение 2 cos 2x cos(-x+2y). Используя отмеченное в правой части слайда свойство, получаем окончательный вид выражения cos(x+2y) + cos(3x-2y)= 2 cos 2x cos(x-2y).


Далее выводится формула разности косинусов. В правой части слайда напоминаются формулы, которые необходимо помнить для выведения формулы преобразования разности косинусов cos (x+y)= cos x cos y-sin x sin y, а также cos (x-y)= cos x cos y+sin x sin y. Разность синусов представляется с аргументами в виде суммы и разности cos(s+t) - cos(s-t). С помощью формул косинуса суммы и разности преобразуем разность косинусов. После приведения подобных слагаемых получаем cos(s+t) - cos(s-t)=-2sin s sin t. Для получения формулы нужного вида вводим дополнительные переменные х и у, через которые можно выразить s и t - s=(х+у)/2, а t=(х-у)/2. Подставив выражения вместо переменных получаем формулу преобразования cos x-cos y=-2 sin (x+y)/2 sin (x-y)/2.
На слайде 11 описывается решение задания, в котором необходимо упростить выражение cos(7π/18)- cos(π/9). Задание решается прямым применением формулы разности косинусов. После вычислений и сокращений результатом упрощения становится выражение cos(7π/18)- cos(π/9)=-√2sin(5π/36).


В конце презентации рассматривается решение двух уравнений. На слайде 12 описывается решение cos 6x + cos 2x=0. Чтобы решить уравнение, левая часть преобразуется с использованием формулы суммы косинусов. После подстановки аргументов и выполнения вычислений уравнение принимает вид 2cos 4x cos 2x=0. Из полученного уравнения следует, что оно будет справедливо при cos 4x=0 или cos 2x=0. Решение первого уравнения x=π/8 + πn/4 для любого целого n. Из второго уравнения получаем еще значения, удовлетворяющие требованию уравнения x=π/4 + πn/2. Таким образом, получили два выражения для решения уравнения x=π/8 + πn/4 и x=π/4 + πn/2, действительные для любого n.
Далее описывается решение уравнения sin 7x + sin 3x – sin 5x=0. В правой части слайда отображаются формулы, знание которых необходимо для решения задания – преобразование суммы синусов, определение аргумента по известному sin t=a при а=0 – аргумент t=πk, а также определение аргумента из известного cos t=a при |a|<=0, который равен t=+-arccos a + 2πk. Первая часть уравнения представляет собой сумму синусов, для преобразования которой можно применить известную формулу. После подстановки аргументов и проведения преобразования получаем уравнение вида sin 5x(2 cos 2x – 1)=0. Решение сводится к решению двух уравнений sin 5x=0 и 2 cos 2x – 1=0. Из первого уравнения решение x=πn/5, а из второго x=+-π/6 + πk для любого целого n. Таким образом, решение определяется двумя формулами.


Презентация «Преобразование сумм тригонометрических функций в произведения» служит наглядным пособием для проведения урока алгебры в школе. Также данный материал может помочь учителю в достижении учебных задач в ходе дистанционного обучения. Последовательное изложение темы и детально разобранное решение примеров может помочь ученику самостоятельно освоить тему урока.
| Автор | |
|---|---|
| Дата добавления | 27.07.2014 |
| Раздел | Алгебра |
| Подраздел | Презентация |
| Просмотров | 6354 |
| Номер материала | 811 |