
Презентация "Применение производной для исследования функций на монотонность"

Краткое описание документа:
Презентация «Применение производной для исследования функций на монотонность» является наглядным пособием для ведения урока математики по этой теме. Пособие помогает представить учебную информацию в виде, наиболее удобном для усваивания. Чтобы уметь исследовать функцию на монотонность, нужно уметь строить ее график, находить производную, уметь вычислять производную в заданных точках. Тема сложная, поэтому учителю необходимо использовать все инструменты, повышающие наглядность исследований и демонстрации практического применения изученного материала.
Презентация одна из наиболее эффективных форм представления учебного материала. В данном материале наглядно представлены графические построения. Для большей понятности объяснения используются анимационные эффекты. В презентации есть возможность важные детали построений, понятия в определениях выделяются ярким цветом, теоремы подаются в рамке для лучшего их запоминания. Используя это наглядное пособие, учителю не нужно применять дополнительные инструменты обучения, вспомогательные материалы. Демонстрация помогает удержать внимание учеников на изучении предмета.
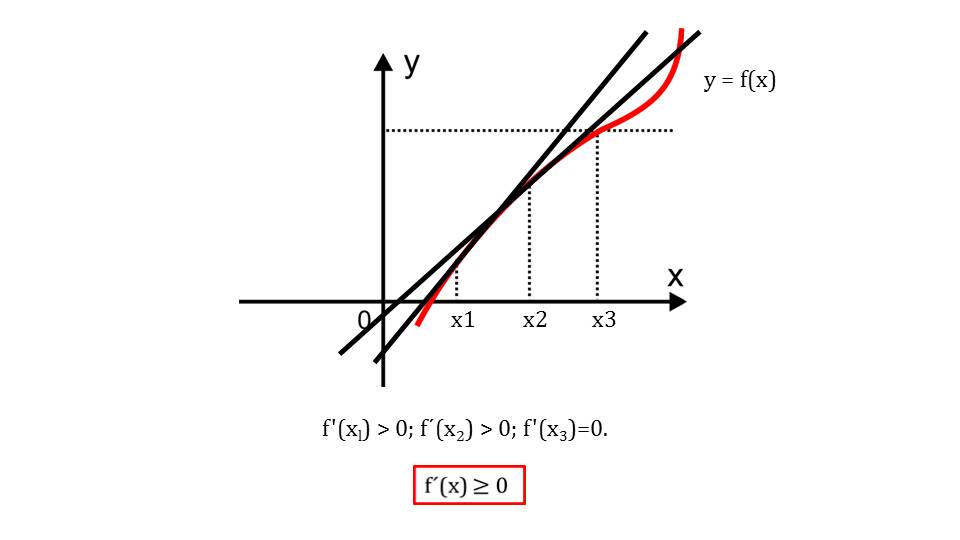
Демонстрация начинается с построения на координатной плоскости графика некоторой функции y=f(x). Мы видим функцию, значения которой постоянно растут с увеличением аргумента. На графике отмечены точки х1, х2, х3. В этих точках вычисляется производная функции. Отмечается, что производные в данных точках положительные или равны нулю, то есть f΄(x1)>0, f΄(x2)>0 и f΄(x3)=0. Для этой функции можно отметить, что производная f΄(x)>=0.
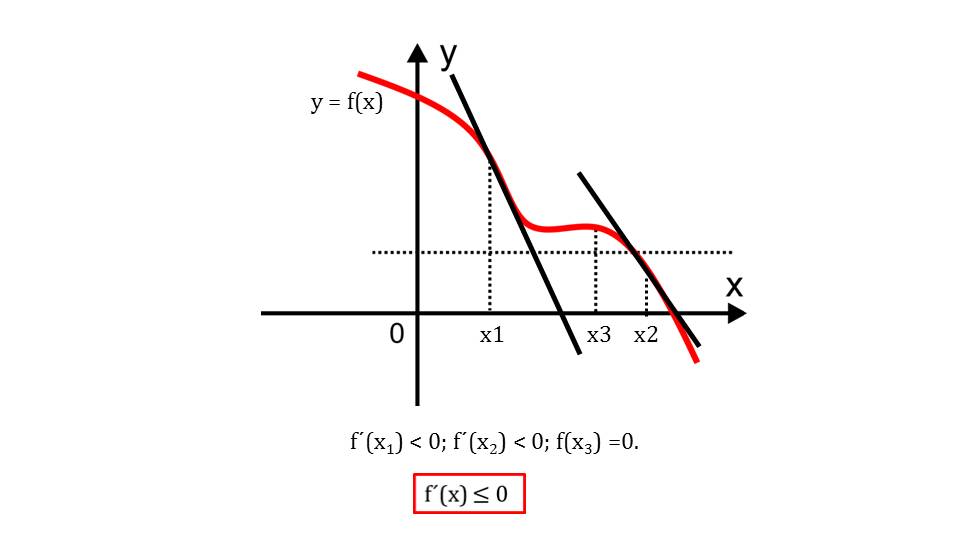
На втором слайде на координатной плоскости построен график функции y=f(x), значения которой все меньше с каждым следующим значением аргумента. На графике отмечены точки х1, х2, х3, к которым построены касательные, и в которых отмечен знак производной. Указано, что f΄(x1)<0, f΄(x2)
<0 и f΄(x3)=0. То есть для данной убывающей функции характерно f΄(x)<=0.


Продемонстрированное поведение производной функции подводит к понятиям возрастания и убывания функции на промежутке. На слайде 3 ученикам представлены теоремы 1 и 2, определяющие такое поведение. В теореме 1 указано, что если для всех точек открытого промежутка Х верно неравенство f΄(x)>=0, а число производных, равных нулю, конечное, то можно утверждать, что функция на Х возрастает. Вторая теорема дает характеристику убывающей функции на промежутке Х, отмечая, что функция является убывающей в промежутке Х, если для каждой точки промежутка выполняется неравенство f΄(x)<=0, а число точек, в которых производная равна нулю, конечное.
Для закрепления полученных знаний приводится пример, в котором требуется доказать , что функция y=2x5+√5x3-4 на всей числовой прямой возрастает. Чтобы решить задачу, сначала находим производную от данной функции. Соответствующее выражение f΄(x)= 10x4+3√5x2. Анализируя данное выражение, можно утверждать, что в любой точке числовой оси его значение будет положительно или равно нулю, то есть 10x4+3√5x2>=0. Поэтому, используя теорему 1, можно ответить на вопрос задачи – функция возрастает по всей координатной прямой.
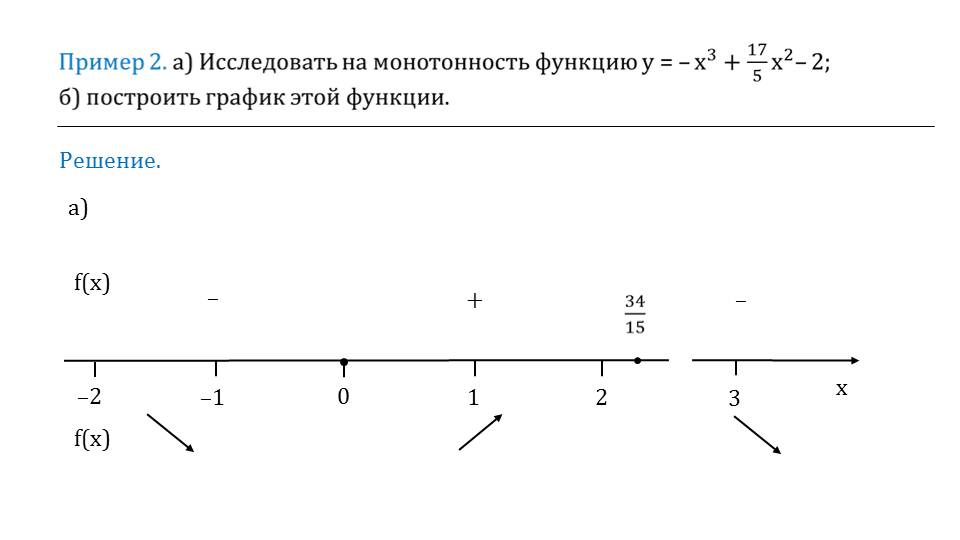
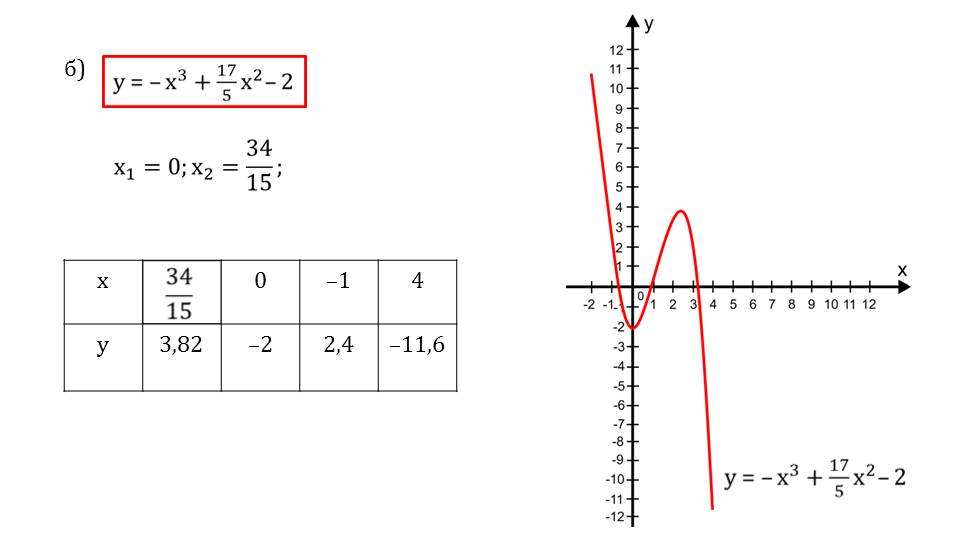
На слайде 5 необходимо исследовать функцию y=-x3+(17/5)x2-2 на монотонность и построить график функции. Для решения необходимо умение исследовать функцию на монотонность

 .
.
Что это означает указано на слайде 6, где выделено, что исследовать функцию на монотонность означает определить промежутки, на которых эта функция убывает или возрастает. Поэтому решение задания сводится к определению знака производной на числовой оси. Рисунок на слайде 7 демонстрирует числовую ось с обозначенными на ней интервалами, на которых отмечен знак производной и стрелкой показано направление графика – убывающий или возрастающий. Основанием для таких выводов служит анализ знака производной функции. На экране отображается выражение, представляющее собой производную функции f΄(x)=-3x2+(34/5)x. После вынесения общего множителя за скобки получаем выражение –х(3х-34/5), из которого легко найти х1=0, х2=34/15. Очевидно, знак производной сохраняется отрицательным или значение нулевое на промежутках (-∞,0] и [34/15,+ ∞). Поэтому на этих промежутках функция является убывающей. Положительным знак производной будет только на промежутке [0,34/15]. Поэтому на этом промежутке функция является возрастающей.
На слайде 9 демонстрируется вторая часть задания – построение графика функции y=-x3+(17/5)x2-2. В точках х1=0, х2=34/15 график функции поворачивается и меняет направление. Вычислив несколько значений функции в различных токам, принадлежащих разным промежуткам, заполняется таблица, с помощью которой строится график функции.
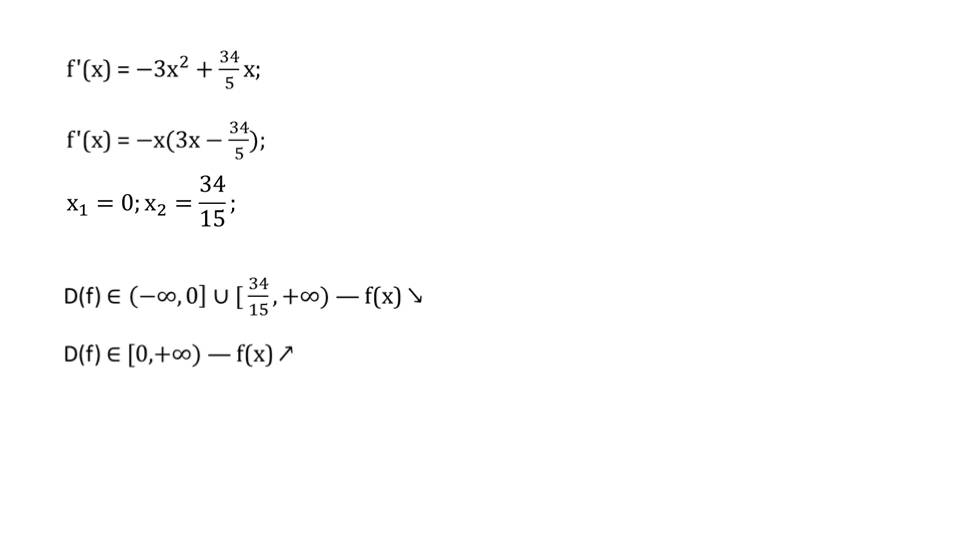
На последнем слайде демонстрируется теорема 3 о признаке постоянства функции. Утверждается, что функция, для всех точек промежутка Х которой верно равенство f΄(x)=0, будет постоянной на этом промежутке.
Пример 3 описывает доказательство тождества sin2x+cos2x=1. Необходимо доказать, что левая часть тождества является постоянно равной 1 при любых значениях х. Левая часть представляется функцией y= f(x), в которой f(x)=sin2x+cos2x. Определяем производную данной функции. Представив каждое слагаемое в виде произведения, применяем формулы для нахождения производной произведения. После приведения подобных слагаемых производная f΄(x)=0. То есть эта производная принимает значение С – некоторой константы. В х=0 значение функции при подстановке аргумента будет f(0)=1, то есть С=1. Поэтому доказываемое тождество sin2x+cos2x=1 действительно справедливо.

Презентация «Применение производной для исследования функций на монотонность» может использоваться на уроках математики в школе. Также данное пособие может быть полезным учителю, осуществляющему обучение дистанционно. Материал может быть рекомендован ученикам, самостоятельно осваивающим предмет.
| Автор | |
|---|---|
| Дата добавления | 27.07.2014 |
| Раздел | Алгебра |
| Подраздел | Презентация |
| Просмотров | 2721 |
| Номер материала | 821 |