
Презентация "Применение производной для поиска наибольшего, наименьшего значения"

Краткое описание документа:
Презентация «Применение производной для поиска наибольшего, наименьшего значения» предназначена для обеспечения наглядности объяснения данной темы учителем. В ходе презентации раскрывается смысл понятий наибольшего, наименьшего значения, приводятся примеры использования данных знаний в решении практических задач. При помощи наглядного пособия учитель дает представление ученикам об одном из важнейших аспектов исследования функции, формируется умение исследовать функцию, строить ее график, использовать знания о производной функции для решения аналитических заданий.
Подавая информацию в форме презентации, учитель использует инструмент, включающий группу приемов для удержания внимания учеников на изучении предмета, улучшения запоминания подаваемой информации, ее усвоения. Для удобства подачи материала используются анимационные эффекты. Все рисунки выполнены точно, в цвете, хорошо будут видны и понятны всем ученикам в классе. Выделение цветом помогает ученикам запомнить определения, формулы, обратить внимание на существенные детали при построении.


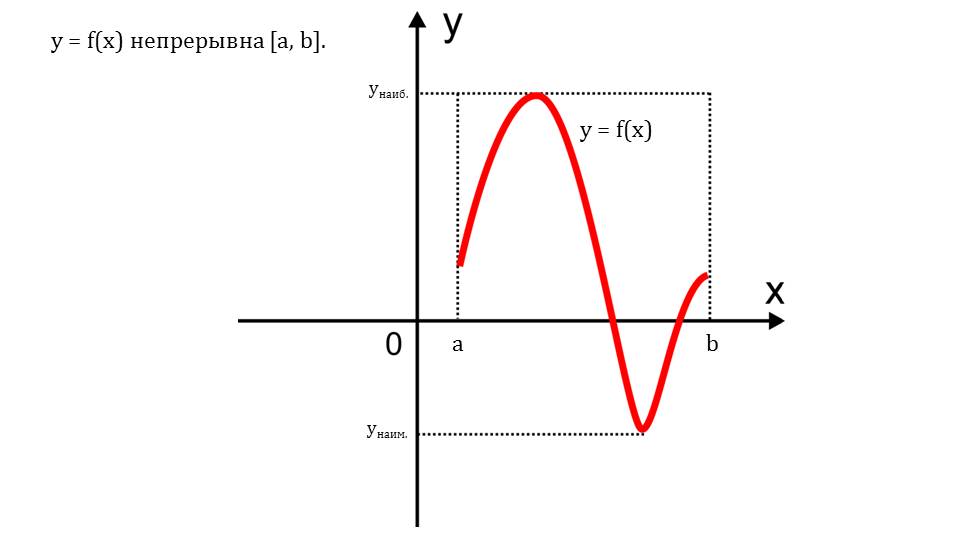
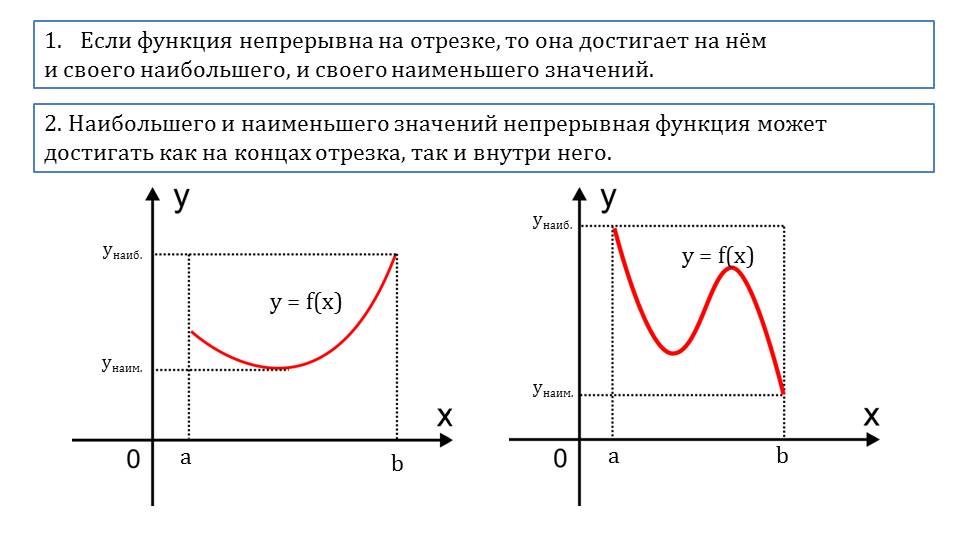
Презентация начинается с демонстрации графика функции и непрерывности ее на некотором промежутке [a,b]. Отмечается, функция определена на данном промежутке, непрерывна, а также имеет самое большее, и самое меньшее значения в определенных точках. Отмечается особенность непрерывной функции на некотором отрезке. В замечании указано, что, у непрерывной функции имеется самое большее и самое меньшее значения на этом отрезке. При этом они могут находиться на концах отрезка, а также внутри области определения. Данные замечания проиллюстрированы построениями. На первом рисунке указан график функции, где наименьшее значение располагается во внутренней части отрезка области определения, а наибольшее значение обнаружено на конце отрезка. Второй рисунок представляет график непрерывной функции, во внутренней области которой лежат точки экстремума, однако наибольшее, а также самое меньшее значение функция принимает на концах этого отрезка. Также замечено, что если экстремальное значение располагается внутри отрезка области определения, то оно совпадает со стационарной или же критической точкой. С помощью рамки выделено для запоминания, что стационарные точки есть точками максимума или минимума. Критическими точками называются такие точки, где производная не существует.

На слайде 4 ученик знакомится с алгоритмом поиска наименьшего, наибольшего значения. В алгоритм входят 3 этапа – определение производной функции, нахождение особых точек функции на ab и вычисление значений на концах отрезка, и еще в точках, найденных на втором этапе. Далее среди этих значений выбирается наибольшее и наименьшее.
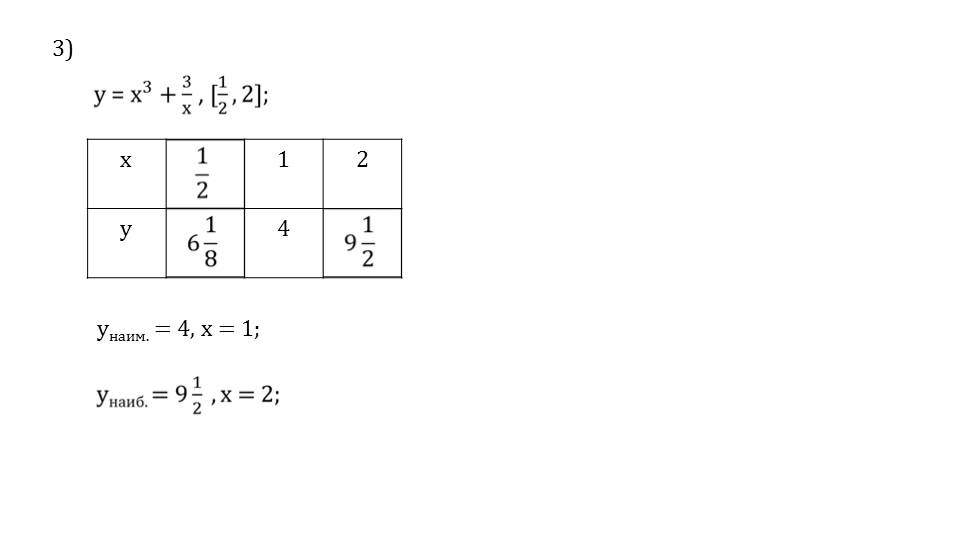
Затем рассматривается пример нахождения на заданном отрезке экстремальных значений функции для у=х3+3/х. Согласно изученному алгоритму, сначала определяется производная функции. В данном случае она равна у′=(х3+3/х)′=(3х4-3)/х2. Затем находятся точки, где производная равна нулю у′=0. Это точки х=1 и х=-1.

Далее находятся значения функции в особых точках, найденных как стационарные и критические. После сравнения результатов, можно сделать вывод, что наименьшее значение функции – точка (1,4), а наибольшее значение функция принимает в точке (2;9+½).
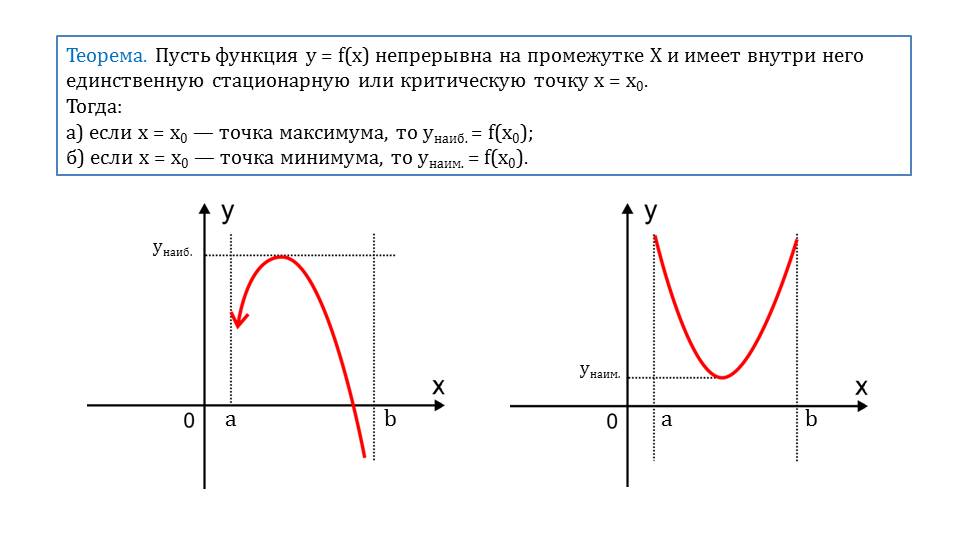
На следующем слайде демонстрируется еще одна особенность критических точек. Теорема утверждает, что в случае существования внутри промежутка единственной особой точки (при непрерывности функции), когда точка является максимумом функции на промежутке –она есть на этом промежутке наибольшим значением, а когда она является минимумом, то и наименьшим значением функции.
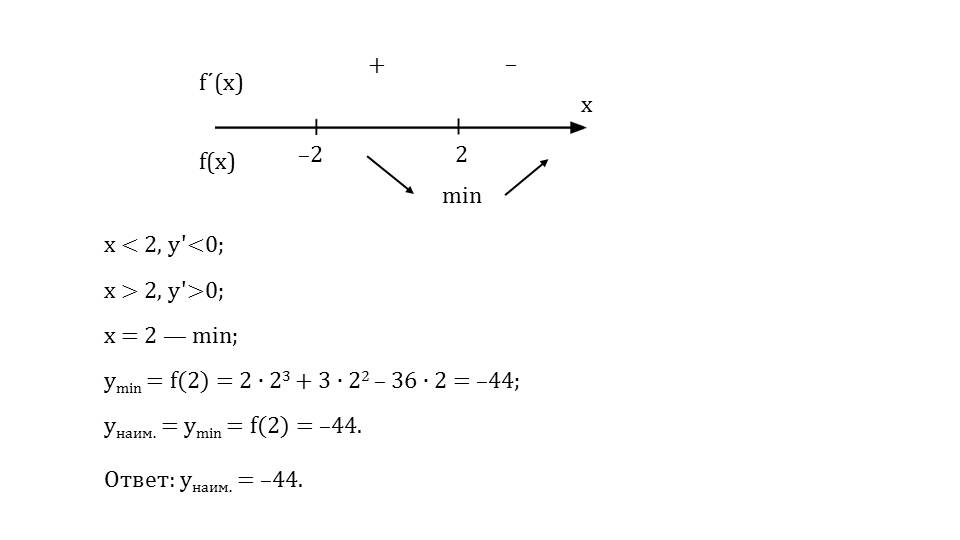

Затем на слайде 8 приводится пример поиска наименьшего, наибольшего значения у=2х3+3х2-36 на промежутке [-2;+∞). На первом этапе решения находят производную функции у′=(2х3+3х2-36)′=6х2-6х-36. Приравняв производную у нулю, находим решения. На числовой прямой отмечают данные точки и анализируется знак производной. Около точки х=2 функция из убывающей становится возрастающей, поэтому данная точка представляет собой точку минимума.


После подстановки значения аргумента находим значение. В результате получаем ответ – наименьшее значение у=2х3+3х2-36 на промежутке [-2;+∞) будет у=-44. На слайде 10 представлен российский математик Чебышев П.Л., сделавший большой вклад в теории исследования функции. В своих трудах он отметил, что методы науки, позволяющие решать общую задачу для практического применения с целью получить наибольшую выгоду при имеющихся средствах, являются очень важными. Данное высказывание отмечено на отдельном слайде.


В следующей части презентации раскрывается практическая ценность изученного материала. При решении задач применяются методы математического моделирования, позволяющие с помощью математического аппарата найти решение задач. На слайде 12 представлены этапы математического моделирования, среди которых составление модели, операции с ней и ответ на требование задания. Первый этап включает выделение оптимизируемой величины, переменной и выражение у через х. В результате таких действий будет построена математическая модель задачи, выраженная функцией и областью определения на некотором промежутке Х. На II этапе предлагается отыскать наибольшее, наименьшее значение математической модели. На третьем этапе получается ответ, полученный из условия.

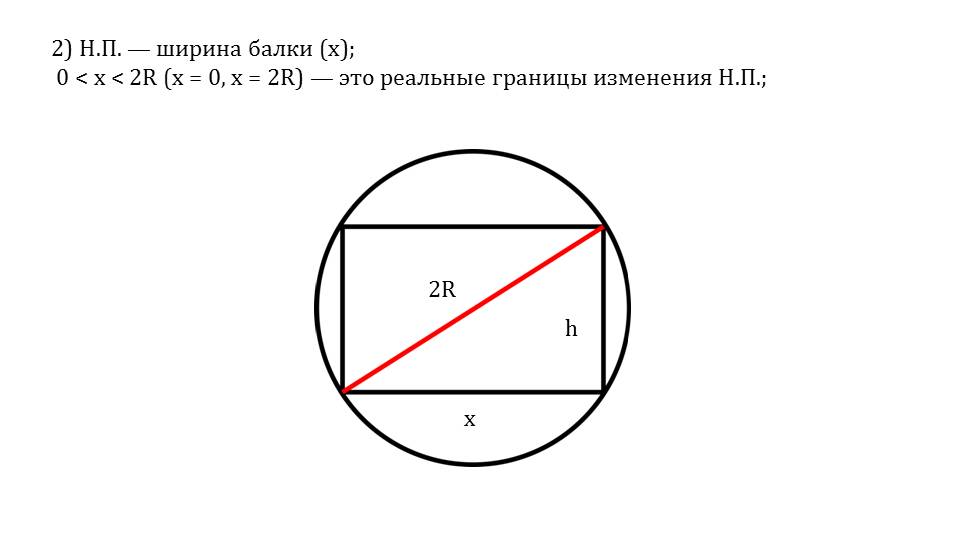
Для представления математического моделирования берется задача о нахождении радиуса сечения балки самой большей прочности. Согласно алгоритму математического моделирования, первым делом отмечается оптимизируемая величина – прочность. Введенной переменной является ширина балки, изменяющаяся в границах х=0, х=2R. Объяснение сопровождается рисунком, в котором видно изменение радиуса. На первом этапе также описывается математическая модель х2-h2=4R2. На втором этапе определяется функция y=kx(4R2-x2), x[0, 2R]. Для поиска наибольшего значения ищем, в каких точках производная нулевая. Это точки х1=2R/√3 и х2=-2R/√3. После подстановки значений аргумента в функцию, находят ее значение у наиб.=f(2R/√3) . На третьем этапе после подстановки полученного значения х в уравнение, получаем искомую величину р=сечения балки самой большей прочности h/x=√2≈1,4.


Презентация «Применение производной для поиска наибольшего, наименьшего значения» может применяться на уроках математики для повышения эффективности обучения.

Также данный материал может стать удобным инструментом дистанционного обучения. При необходимости углубить понимание предмета материал может быть рекомендован ученику для самостоятельного рассмотрения.
| Автор | |
|---|---|
| Дата добавления | 27.07.2014 |
| Раздел | Алгебра |
| Подраздел | Презентация |
| Просмотров | 4783 |
| Номер материала | 823 |