
Презентация "Применение производной в исследовании функций на максимум и минимум"

Краткое описание документа:
Презентация «Применение производной в исследовании функций. Построение графика функции» является наглядным пособием в помощь учителю математики для проведения урока по данной теме. В ходе презентации ученикам представляется теоретические сведения, необходимые для исследования функции и формируется умение исследовать функцию на экстремумы и монотонность. Пособие помогает повысить эффективность обучения, быстрее достичь учебных задач.
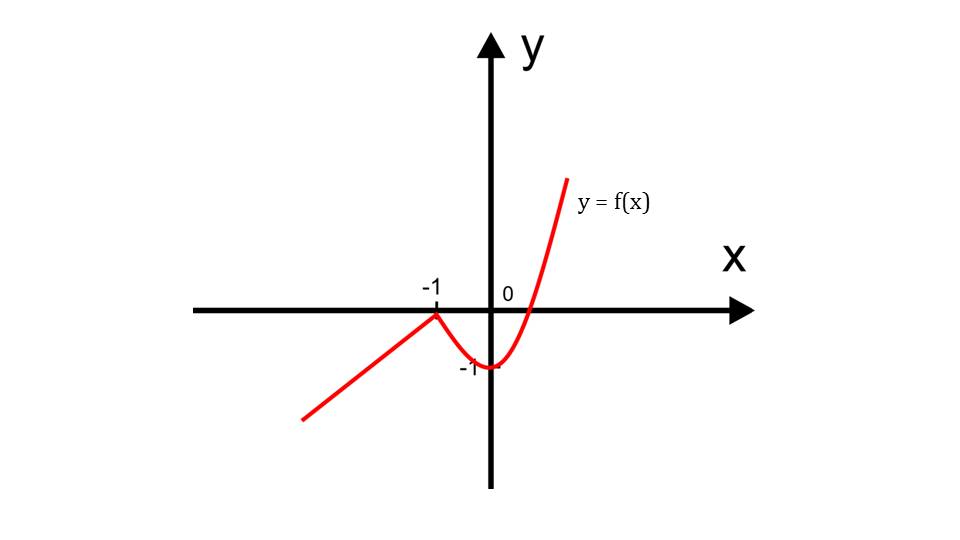

Объяснение учителя по теме обязательно сопровождается рисунками, демонстрацией решения примеров на координатной плоскости. Для этого нужно производить построения с помощью вспомогательных средств. Однако в случае использования презентации, необходимость в таких инструментах отпадает. Анимационные эффекты в презентации помогают упорядочить демонстрацию материала, представить информацию в виде, наиболее удобном на понимания учениками. Информация, поданная в ходе презентации, лучше усваивается и запоминается.
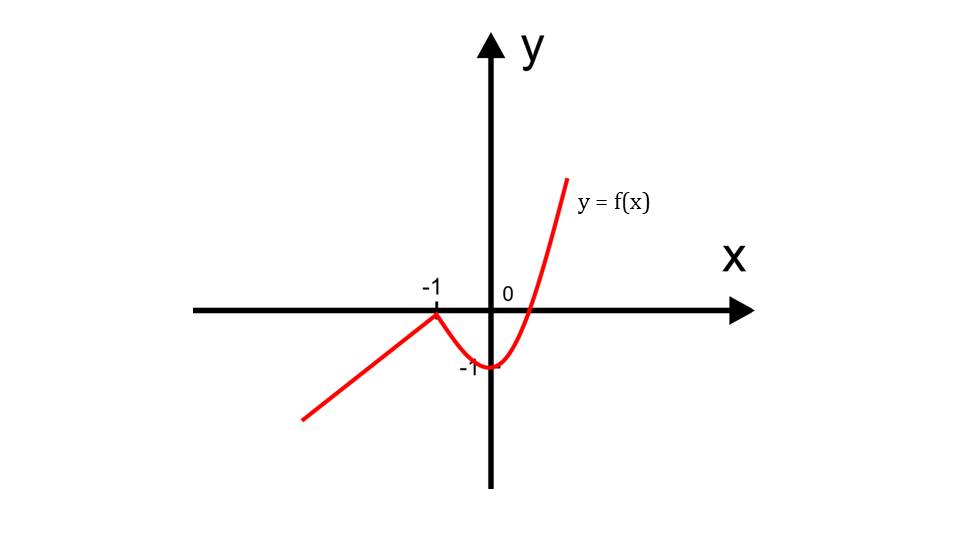

Презентация начинается с напоминания, какие точки важны при исследовании функции. Отмечается, что во время исследования имеет место определение особых точек функции. Отмечается, что для графического представления функции нужно найти экстремумы, другие особые точки, промежутки монотонности, а при необходимости дополнительные точки. Если же функция не является определенной на числовой оси, то следует сначала определить промежутки области определения, разрывы. Также указано, что при исследовании функции следует определить ее четность или нечетность, так как данное свойство дает большие возможности в анализе поведения графика функции. При этом, если функция является симметричной относительно начала координат или одной из осей, построив одну ветвь графика, можно легко достроить вторую.

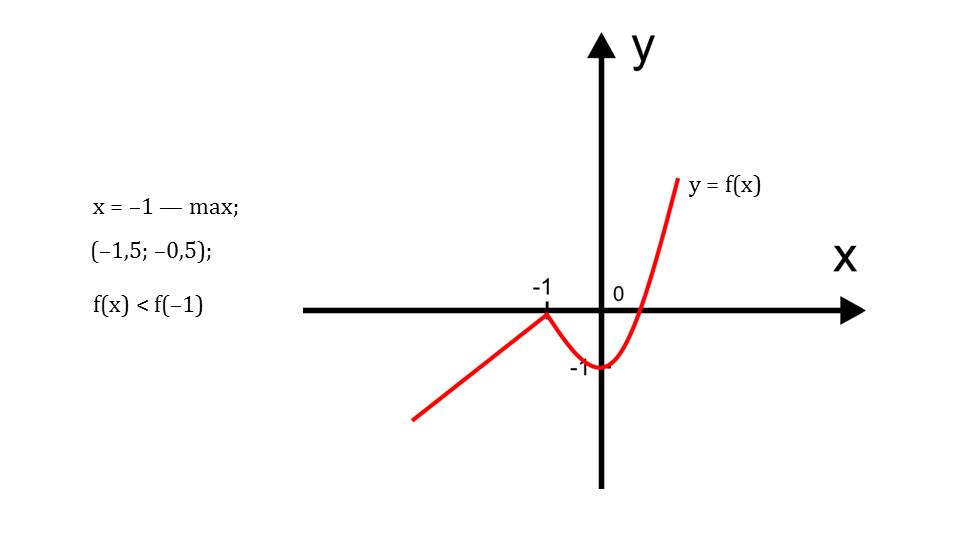
Еще одним важным пунктом исследования поведения функции является построение ее асимптот. Ученикам напоминается, что если для данной функции lim f(x)=b при n→∞, то прямая у=b будет горизонтальной асимптотой функции, которую также нужно очертить при построении графика. Обратное условие – стремление значения функции к бесконечности при стремлении аргумента к некоторому числу означает наличие вертикальной асимптоты графика. Ее также необходимо уметь строить при исследовании функции. На слайде 4 демонстрируется признак имеющейся вертикальной асимптоты, который заявляет о ее наличии в точке а, если знаменатель функции при подстановке этого значения обнуляется.


Изученный материал закрепляется рассмотрением примера, в котором требуется построить график у=8/(4+х2). Согласно алгоритму исследования функции, сначала определяется область определения функции – для данного примера это вся числовая ось. Далее проверяется ее четность. При подстановке отрицательного значения в f(х) получаем f(-х)=8/(4+(-х) 2)= 8/(4+х2)= f(х).
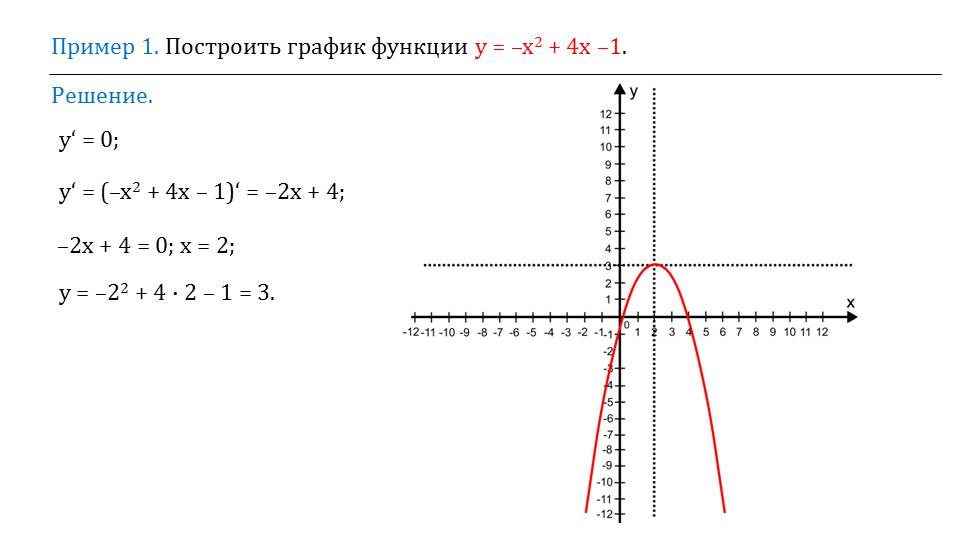

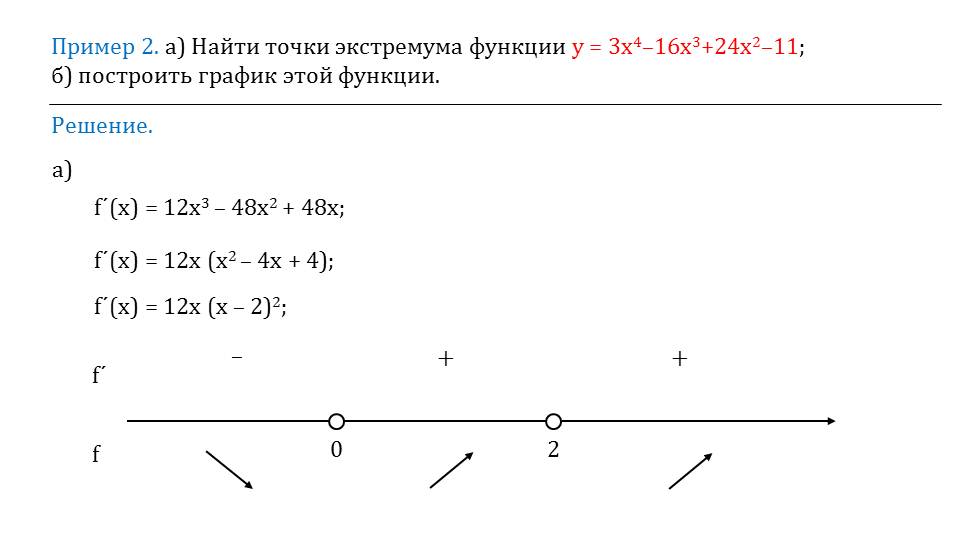
Это говорит о четности функции. Далее рассматривается предел функции при стремлении к бесконечности. На слайде 6 демонстрируется нахождение предела lim 8/(4+х2)=0. Очевидно, что на бесконечности функция стремиться к нулю. Чтобы определить экстремумы функции, нужно найти производную у′=-16х/((4+х2)2). Так как в точках экстремума производная равна нулю, приравниваем полученное выражение к нулю -16х/((4+х2)2)=0. Из уравнения получаем ответ х=0. Решение сопровождаем рисунком числовой прямой, на которой отмечаем точку 0. При подходе слева к нулю мы видим признаки возрастающей функции – положительная производная, справа от нуля функция убывающая (отрицательное значение производной). Значит, точка максимума – «0».
Подстановкой значения в функцию получаем ее значение у=2. Из описанного анализа выводим, на [0;+∞) функция убывает. Не хватает нескольких контрольных точек. Находим их, составляем таблицу из найденных значений (0,2), (1;8/5), (2,1), (3,8/13).
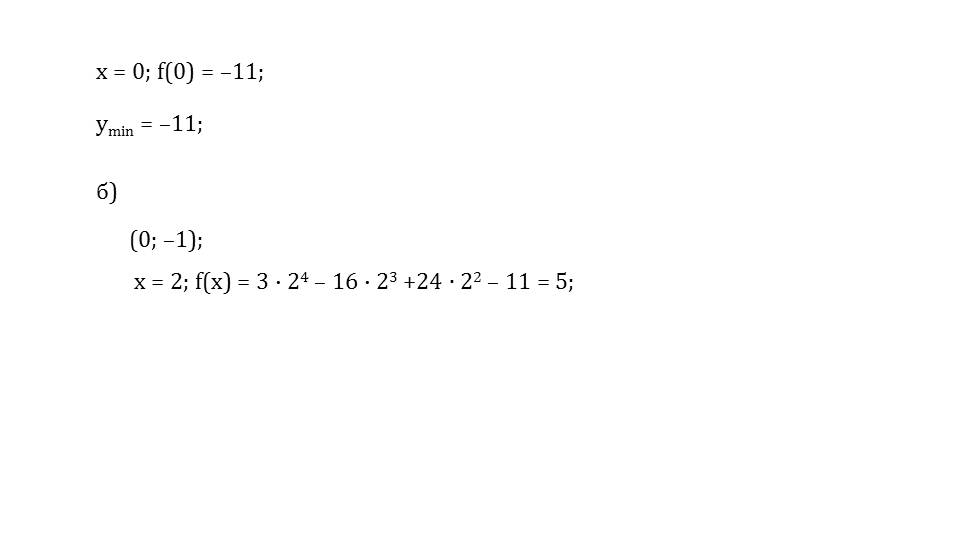
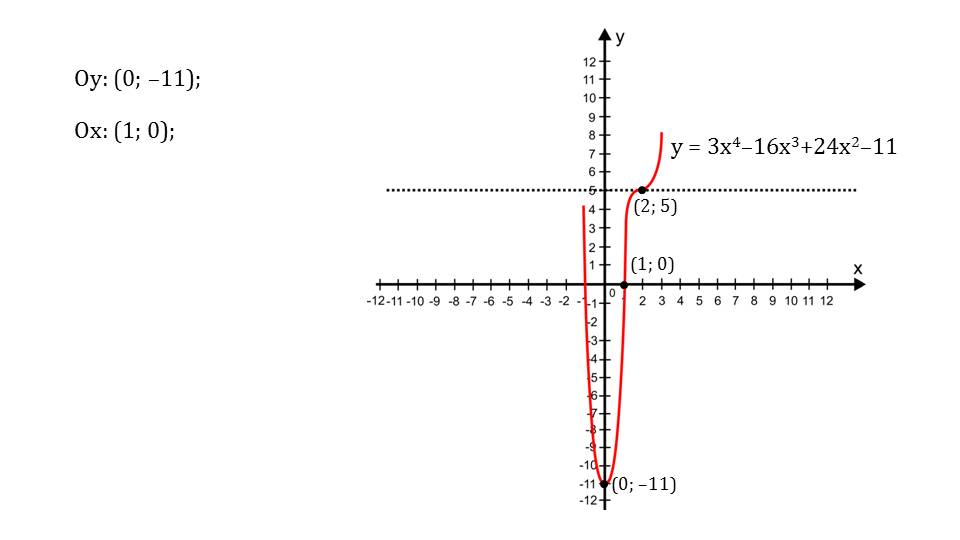
На слайде 9 демонстрируется построенный график функции у=8/(4+х2) на основе данных из ее исследования.
На слайде 10 представлен пример 2, в котором требуется построить график у=(х2+1)/(х2-1). Согласно алгоритму исследования функции, вначале находится область определения. Она охватывает всю числовую ось и разрывается в 1 и -1. То есть область определения обозначена промежутками (-∞;-1), (-1;1), (1;+∞). Вторым пунктом исследования является проверка функции на четность. Для этого ф выражение функции подставляется отрицательное значение f(-x)= f(x).

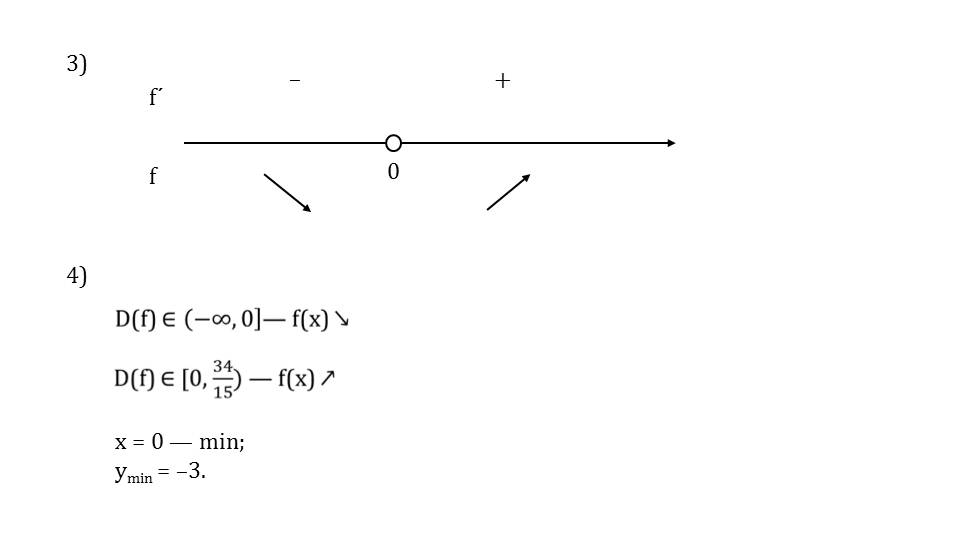
В результате преобразований получили подтверждение признака четности функции. Далее рассматривается нахождение предела функции на бесконечности. Поделив числитель и знаменатель функции на переменную в высшей степени выражения, получили дробь, через которую легче определить значение предела lim(х2+1)/(х2-1)=1 при n→∞. Поэтому у=1 - асимптота графика функции. Далее находим производную функции у′=-2х/(х2-1)2. Чтобы найти точки экстремума, приравниваем выражение к нулю -2х/(х2-1)2=0. Решениями уравнения являются 0, 1, -1. Строится числовая прямая, на которой отмечены точки разрыва. Делается вывод, что на (-∞, 0) функция возрастает, убывающая функция при этом на (0, +∞).


Очевидно, точка (0,-1) является точкой максимума функции. Все значения функции будут положительными числами. Для построения в таблицу заносим несколько вычисленных значений для контрольных точек. На основе исследования функции и дополнительно найденных значений контрольных точек построим график функции. На слайде 14 продемонстрирован построенный график функции, состоящий из трех частей, имеющий горизонтальную и вертикальные асимптоты, проходящие через точки разрыва.
Презентация «Применение производной в исследовании функций. Построение графика функции» может применяться учителем на уроке математики для повышения эффективности обучения. Также материал поможет обеспечить наглядность представления предмета изучения в ходе дистанционного обучения. Презентация может рекомендоваться для самостоятельного рассмотрения ученику, которому требуются дополнительные занятия для понимания предмета.
| Автор | |
|---|---|
| Дата добавления | 27.07.2014 |
| Раздел | Алгебра |
| Подраздел | Презентация |
| Просмотров | 4650 |
| Номер материала | 822 |