
Презентация "Синус и косинус суммы аргументов"

Краткое описание документа:
Презентация «Синус и косинус суммы аргументов» представляет наглядный материал по данной теме для ведения урока алгебры в 10 классе. Пособие предназначено для сопровождения объяснения учителя и наглядно демонстрирует свойства тригонометрических функций суммы аргументов.
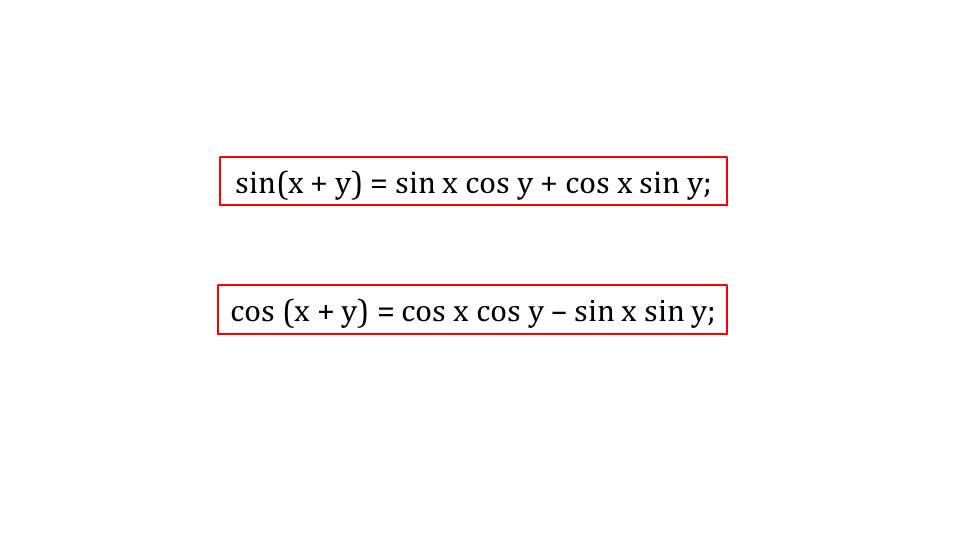
Демонстрация наглядного материала способствует повышению эффективности урока, лучшему запоминанию материала, помогает ученикам освоить предмет изучения. В ходе презентации демонстрируются формулы для определения синуса и косинуса суммы аргументов, рассматривается решение 5 задач на применение знаний формул.
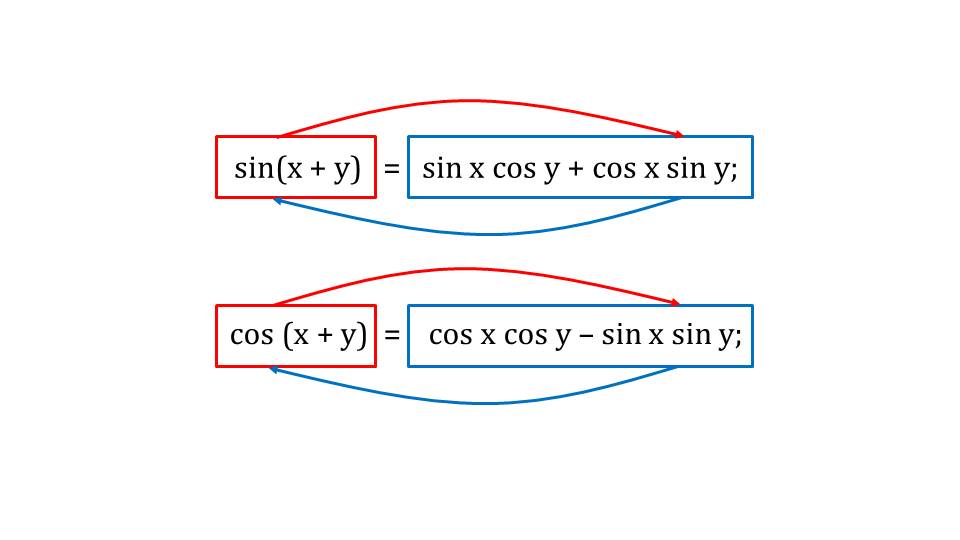
Анимированное представление решения примеров и свойств тригонометрических функций помогает структурировать подачу материала, выделить важные детали для улучшения понимания хода рассуждений при решении заданий. Текст, формулы и графики выполнены в цвете. Это дает возможность акцентировать внимание учеников на объекте, способствует запоминанию учебного материала.


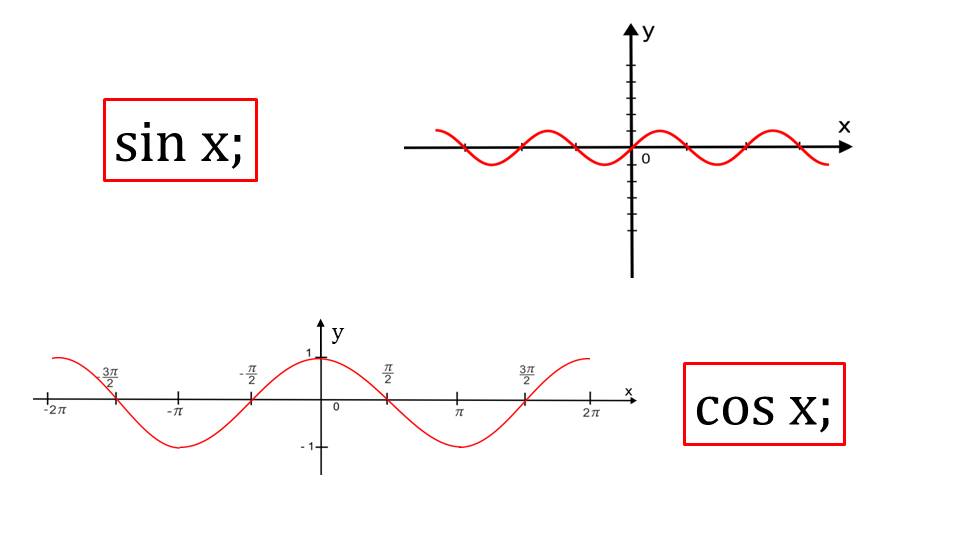
Демонстрация начинается с напоминания ученикам графиков тригонометрических функций – синуса и косинуса. На рисунке данные функции выделены в рамку, их графики, на которых можно наблюдать поведение функций, отмечены красным цветом.
На втором слайде представлены формулы для вычисления синуса и косинуса суммы аргументов: sin (x+y)=sin x cos y+cos x sin y, cos (x+y)= cos x cos y-sin x sin y.


Третий слайд демонстрирует справедливость прямого и обратного преобразования. При помощи стрелок-указателей отмечается, что правая часть можно преобразовать в левую, а формулу вида, представленного в правой части, можно собрать в функцию от суммы аргументов.
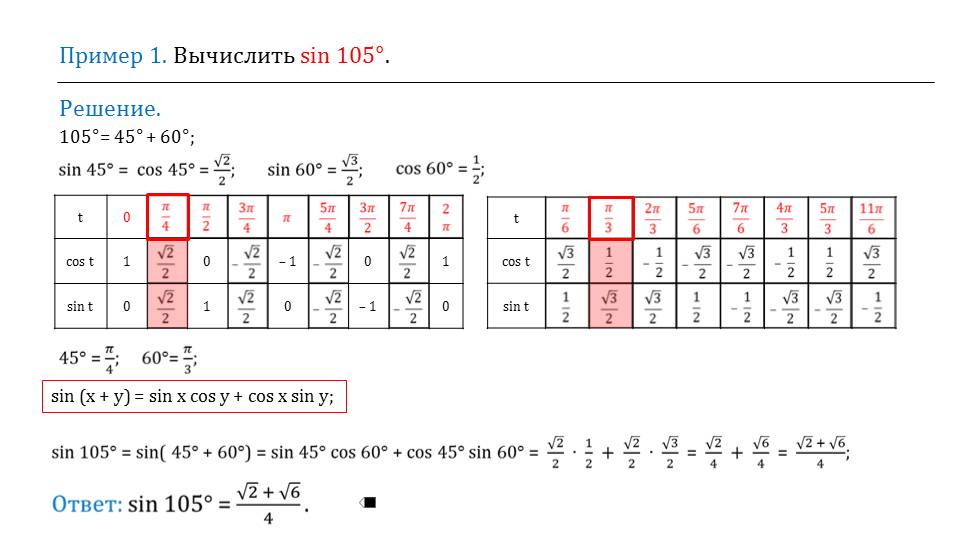
Далее разбираются примеры с использованием изученных формул. На слайде 4 представлен пример вычисления синуса 105°. Очевидно, что данный пример с ходу, основываясь на знании значений простых синусов и косинусов, решить сложно, однако угол можно представить в виде суммы аргументов, от которых легко находятся синус и косинус. Решение примера начинается с представления 150° в виде суммы 45° и 60°. на экране представлена таблица простых синусов и косинусов, из которых можно взять нужные значения. Аргументы в таблице выражены в радианах. Ученикам напоминается, что в радианах заданные углы выражаются 45°=π/4, 60°=π/3. Из таблицы видно, что sin 45°= cos 45°=√2/2, sin 60°=√3/2, cos 60°=1/2. Применяя формулу разложения синуса суммы аргументов, получаем sin 105°= sin(45°+60°)= sin 45° cos 60°+ cos 45° sin 60°. При подстановке табличных значений синусов и косинусов получается значение sin 105°=(√2+√6)/4.
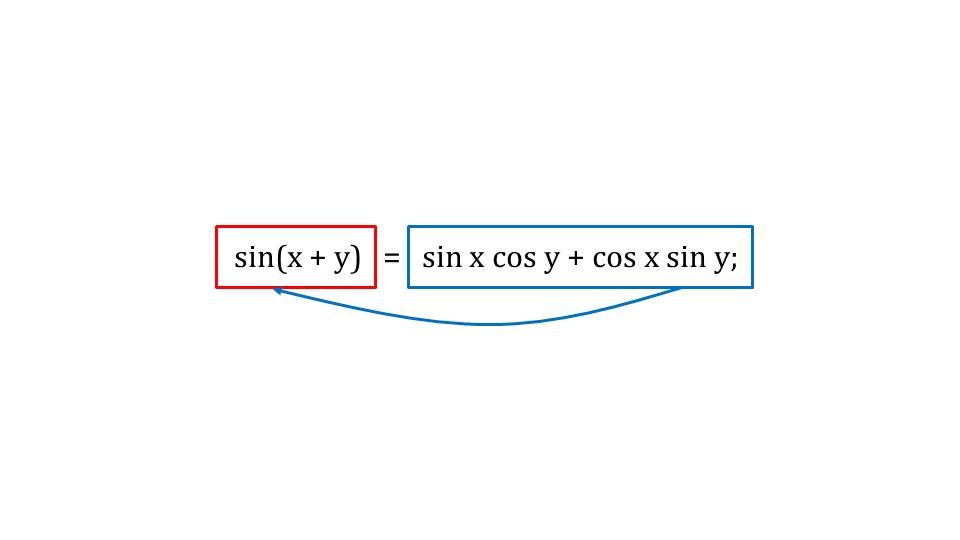
Во втором примере необходимо вычислить значение выражения sin(π/4+х)- cos(π/4+х). В данном выражении представлена разность синуса суммы аргументов и косинуса суммы аргументов. Используя известные формулы, при подстановке соответствующих аргументов получается выражение sin(π/4+х)- cos(π/4+х)= sin π/4 cos х + cos π/4 sin х - cos π/4 cos х + sin π/4 sin х. Из таблицы значений косинусов и синусов выбираем значения sin π/4=√2/2 и cos π/4=√2/2. После подстановки значений в полученное при преобразовании выражение и после сокращения подобных слагаемых получаем значение выражения sin(π/4+х)- cos(π/4+х)=√2 sin х.
Пример 3 описывает вычисление выражения sin 17° cos 13° + cos 17° sin 13°. Очевидно, данное выражение представляет собой вторую часть формулы синуса суммы аргументов, поэтому, применяя данную формулу, из исходного задания получаем более простое выражение sin (17°+13°) = sin 30°. Поэтому значение имеющегося выражения ½.
В примере 4, решение которого представлено на 7 слайде, дается задание вычислить cos(х+у), зная, что cos х = cos у = ½, а значения аргументов лежат в пределах 0<x<π/2, 3π/2<y<2π. Решить данный пример легче всего, применив известную формулу косинуса суммы аргументов и основное тригонометрическое тождество. Зная значение косинуса аргумента, и воспользовавшись основным тригонометрическим тождеством, находим значение sin2 х=1-(1/2)2=3/4. По условию, 0<x<π/2, поэтому синус аргумента принимает на этом промежутке значение sin х=√3/2. Таким же образом определяем sin у. Из основного тригонометрического тождества получаем sin2 у=1-(1/2)2=3/4. Так как у лежит в промежутке 3π/2<y<2π, в нем sin у принимает значения sin у=-√3/2. Подставив полученные значения, после выполнения вычислений получаем значение исходного выражения cos (х+у)=1.

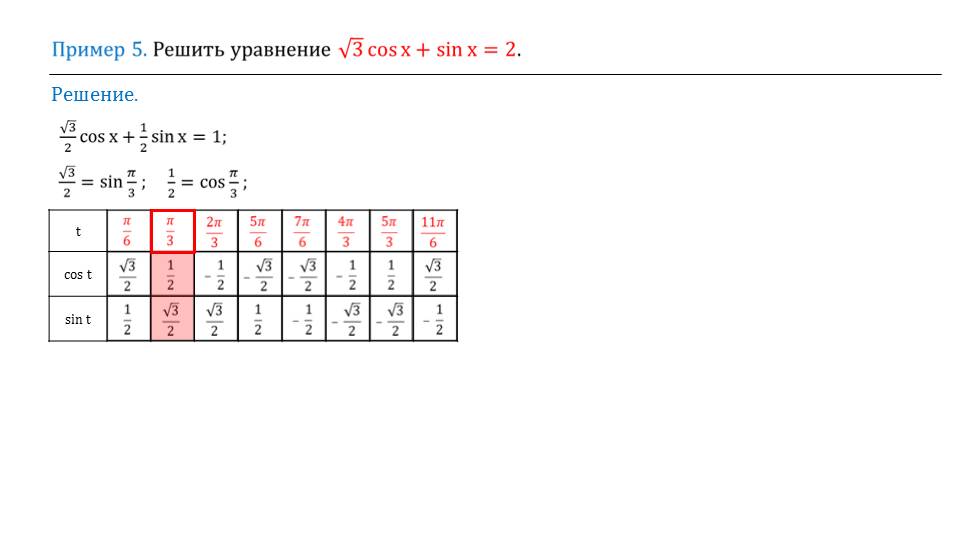
В последнем примере описывается решение уравнения √3 cos х + sin х = 2. Чтобы найти решение данного уравнения, необходимо заметить, что его левую часть можно преобразовать в выражение, аналогичное правой части формулы синуса суммы аргументов. Для этого делим все уравнение на 2, в результате чего получается (√3/2) cos х + (1/2)sin х = 1. Проанализировав значения синусов и косинусов из таблицы, можно подметить, что для угла π/3 синус принимает значение √3/2, а синус ½. Получаем выражение sin π/3 cos х + cos π/3 sin х = 1. После применения формулы синуса суммы аргументов получаем sin (π/3+х) = 1. Зная поведение синуса на координатной плоскости, получаем, что аргумент π/3+х= π/2+2πn, nϵZ. Из данного уравнения легко определить значение аргумента х= π/6+2πn, nϵZ.
Презентация «Синус и косинус суммы аргументов» поможет учителю в проведении традиционного урока в школе. Также данный материал может быть рекомендован ученикам для самостоятельной работы при необходимости дополнительных занятий для освоения предмета изучения. Презентация послужит и инструментом работы учителя в ходе дистанционного обучения.
| Автор | |
|---|---|
| Дата добавления | 27.07.2014 |
| Раздел | Алгебра |
| Подраздел | Презентация |
| Просмотров | 4273 |
| Номер материала | 796 |