
Презентация "Свойства функций"

Краткое описание документа:
Презентация «Свойства функций» включает в себя огромное количество слайдов, которые максимально детально описывают каждое свойство, приводят примеры и иллюстрации. Тема является довольно серьезной и важной.
Первым важным свойством функций является монотонность.

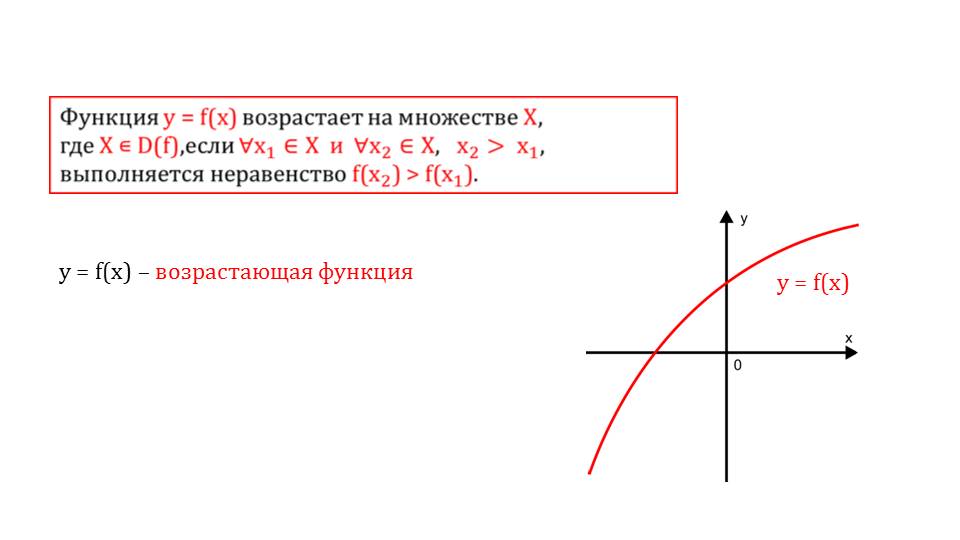
Функция может возрастать или убывать на некотором интервале. На втором слайде описывается возрастающая функция. На графике мы видим, как это выглядит геометрически. Дается определение на данном же слайде. Рекомендуется записать его в тетради.


После этого рассматривается убывающая функция аналогичным образом. Что же такое монотонная функция? Если некоторая функция на множестве х является либо убывающей или возрастающей, то она называется монотонной. Если функция возрастает на определенном интервале (а,b) или убывает, то эти точки указывают на промежутки возрастания или убывания. Функция не обязательно должна быть монотонной.

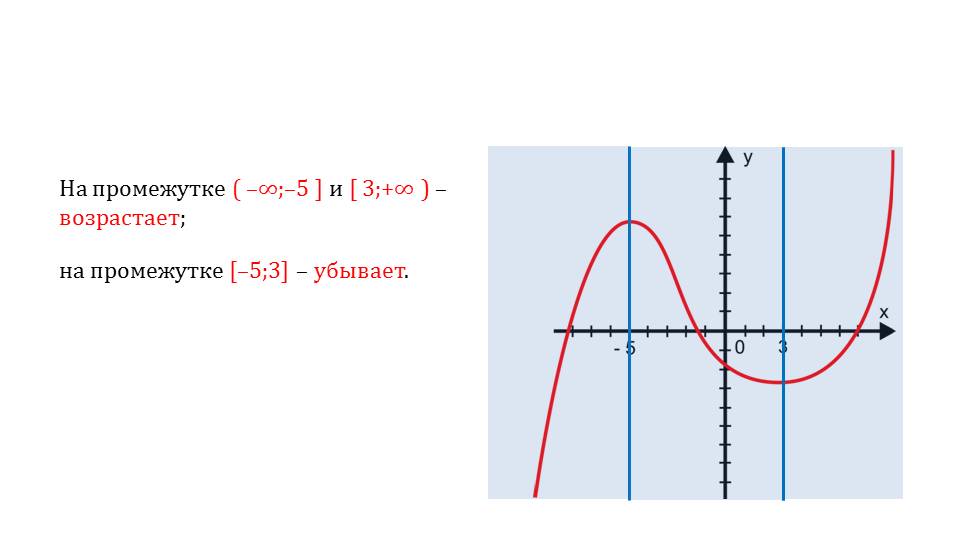
На следующем слайде приводится график, где четко видны интервалы, на которых функция возрастает либо убывает. Нетрудно догадаться, что функция является монотонной. Это наглядно видно на графике.

Чтобы стало еще понятнее, приводится пример. Дается некоторая функция и предлагается исследовать ее на монотонность.
Можно ознакомиться с пошаговым решением, которое опирается на определение ранее рассмотренных определений. Выясняется, что функция убывает на всех числовой прямой.

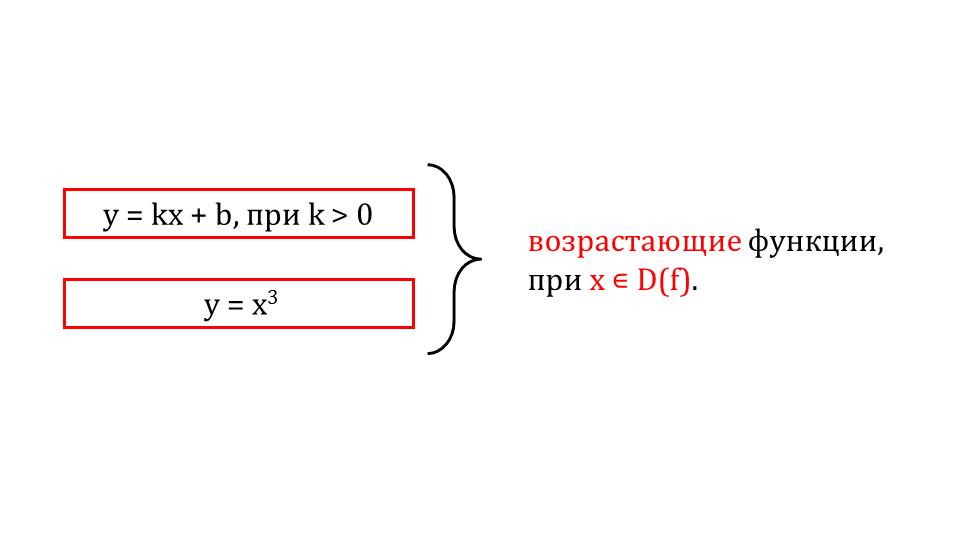
На восьмом слайде приводятся примеры возрастающих функций. Мы видим общий вид их записей. Чтобы это проверить, необходимо взять пример с определенными значениями одной из данных функций и построить графики. Или же, можно доказать это алгебраически, опять же, опираясь на определение возрастающей функции. На этом изучение свойства монотонности заканчивается.
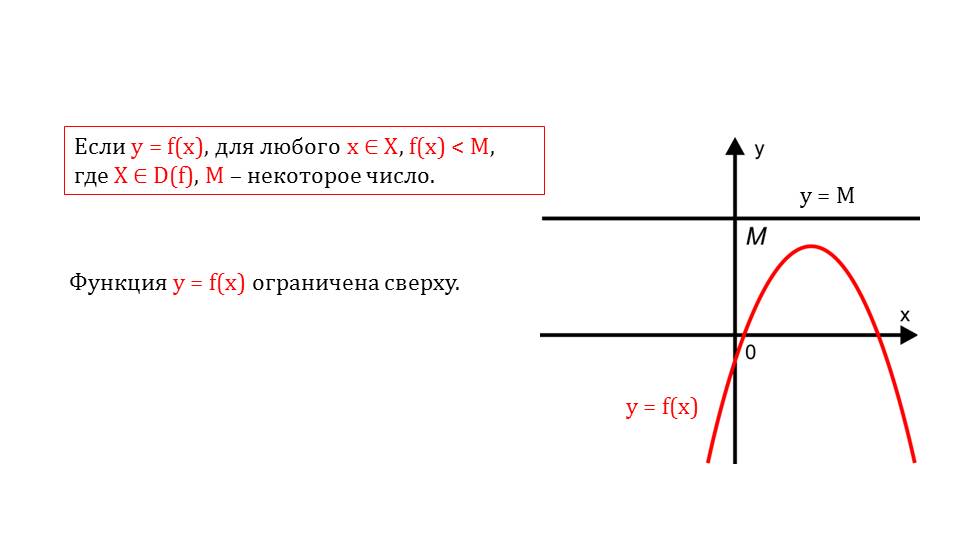
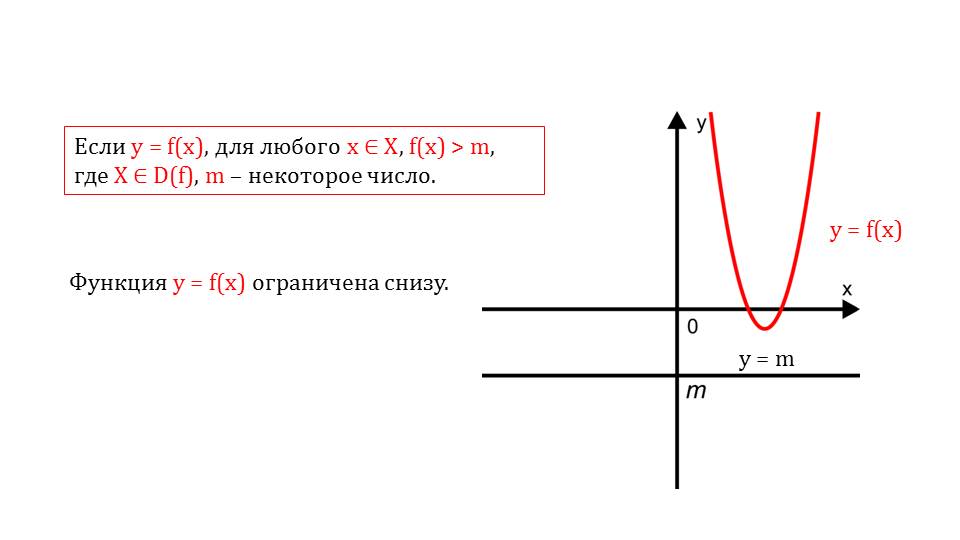
Следующее свойство функций – это ограниченность. Любая функция может быть ограничена как сверху, так и снизу. Изначально рассматривается ограниченность снизу.
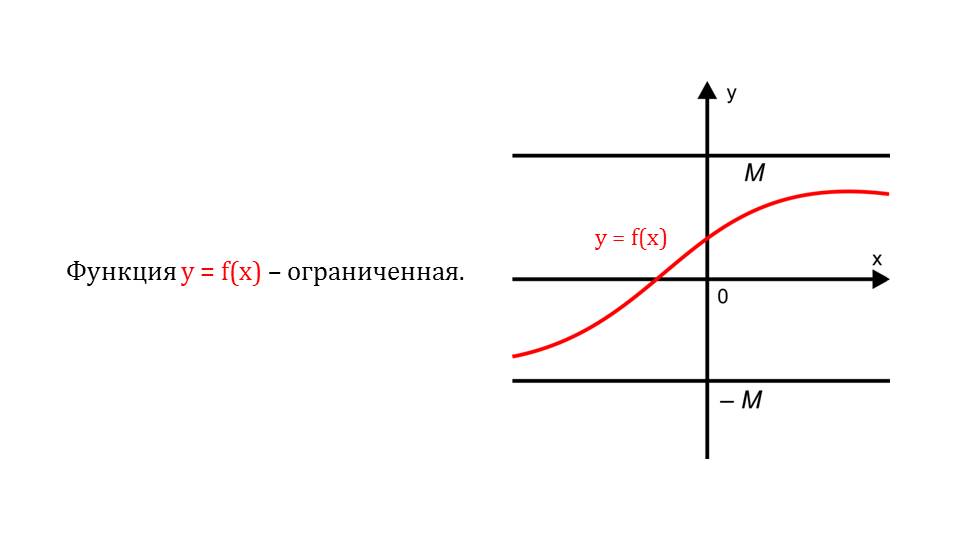
Приводятся графическая демонстрация и текстовое определение. Аналогичным образом далее рассматривается ограниченность сверху. Если некоторая функция ограничена и сверху, и снизу, это указывает на ее ограниченность. На графике функции приводится такой пример.

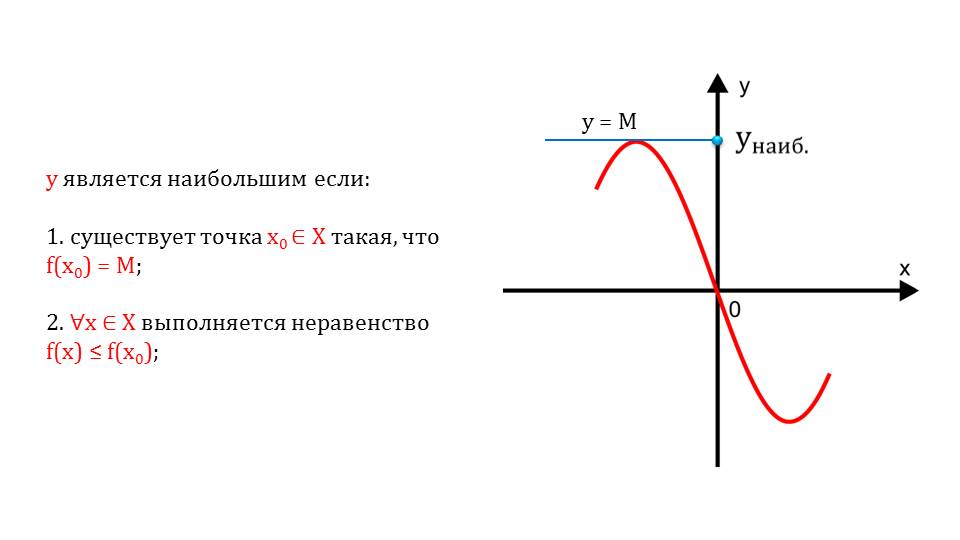
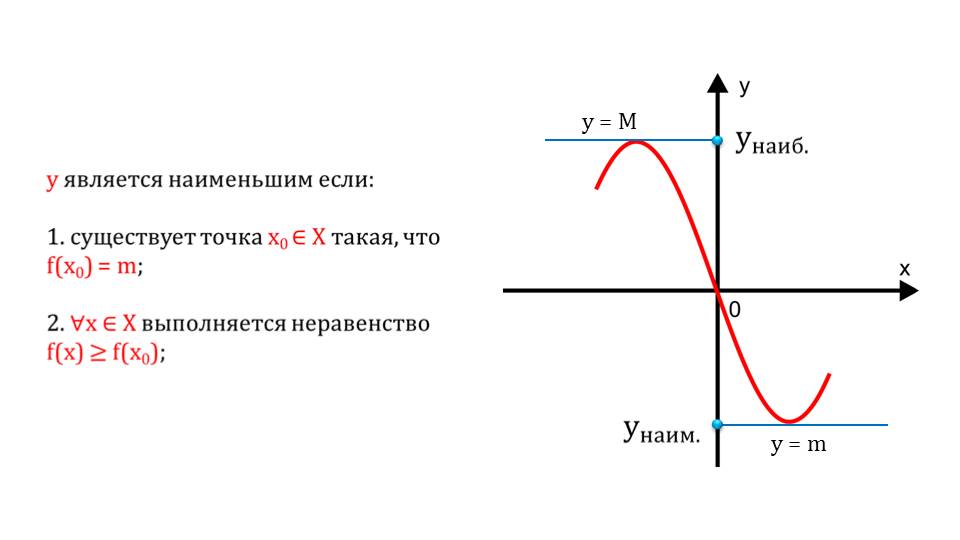
При ограниченных функциях можно найти наибольшее и наименьшее значение. 12-14 слайды посвящены рассмотрению этих вопросов.

Далее приводится некоторое замечание, которое гласит: если функция имеет наименьшее значение, то она ограничена снизу, и, наоборот, если существует некоторый наибольший y, то функция ограничена сверху.

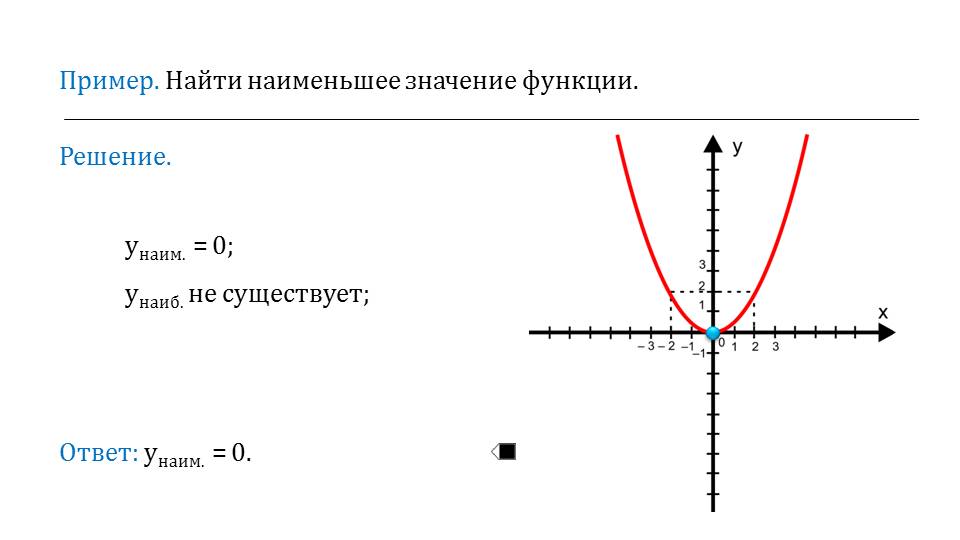
Прежде, чем переходить к изучению следующего свойства, предлагается рассмотреть пример, в котором демонстрируется нахождение наименьшего значения функции. На ее графике легко заметить, что наибольшего значения не существует, то есть она не ограничена сверху.

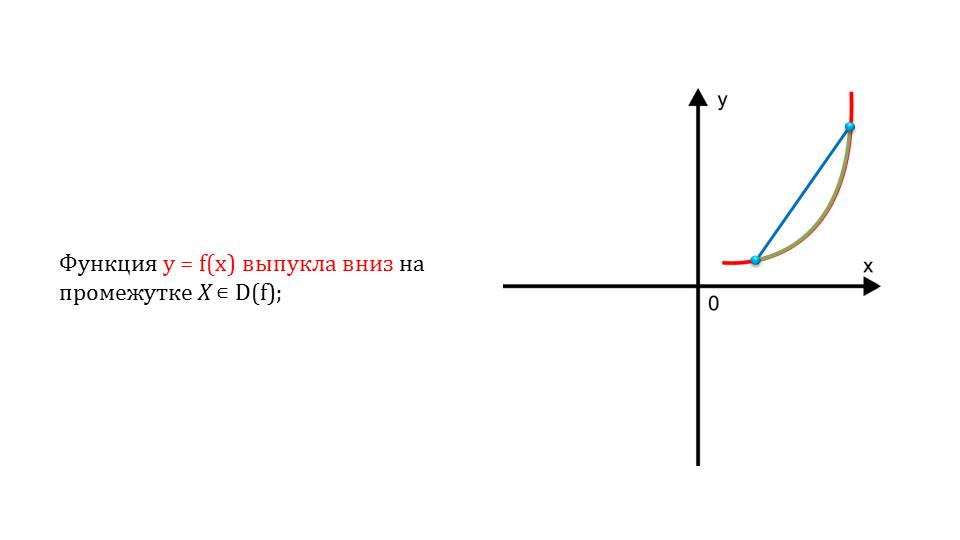
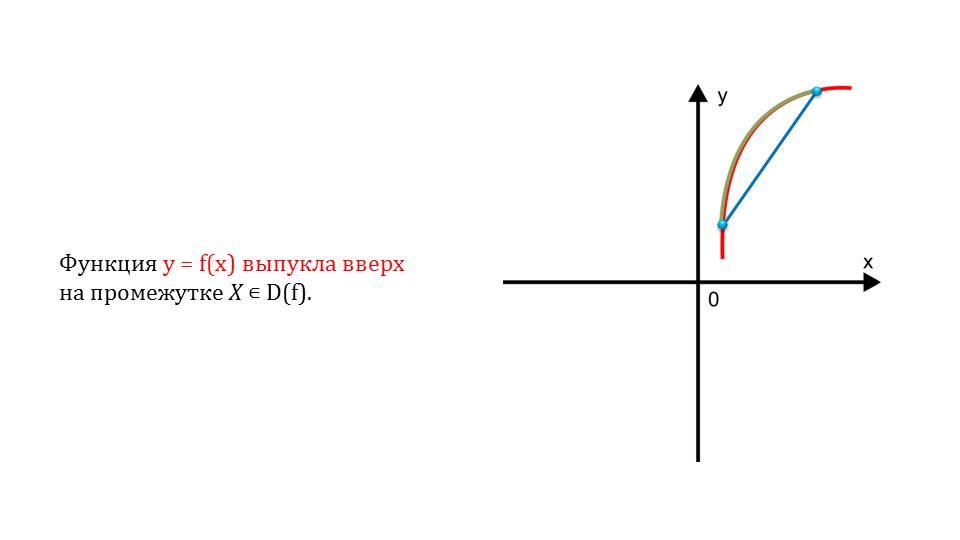
Третье свойство функций – это выпуклость. Рассматривается она, начиная с 17 слайда. Функция может быть выпуклая вниз либо вверх. Это демонстрируется графическим образом.


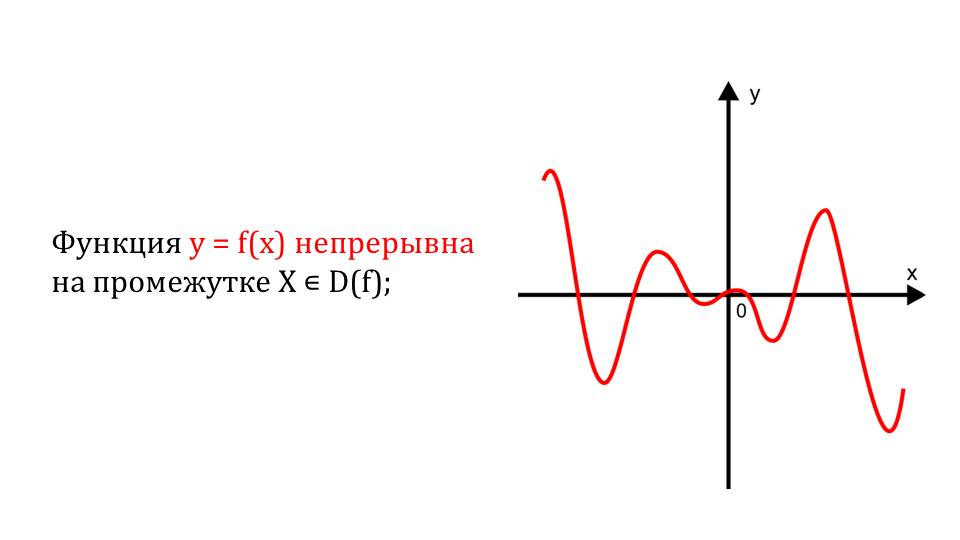
Далее рассматривается свойство непрерывности. В первую очередь дается текстовое определение, которое открывает суть таких понятий, как непрерывность на интервале и непрерывность в некоторой точке. Приводится пример, на котором мы видим некоторый график функции без разрывов и острых углов.
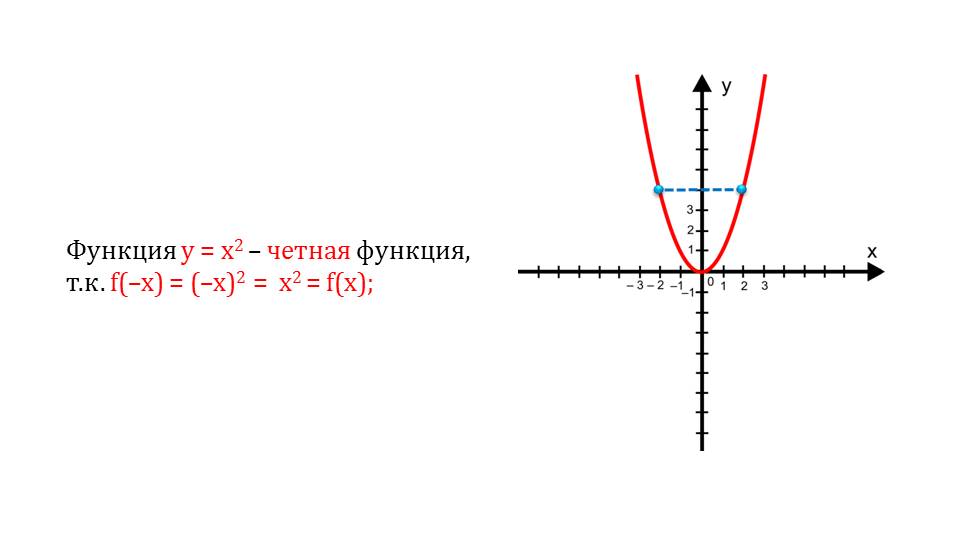

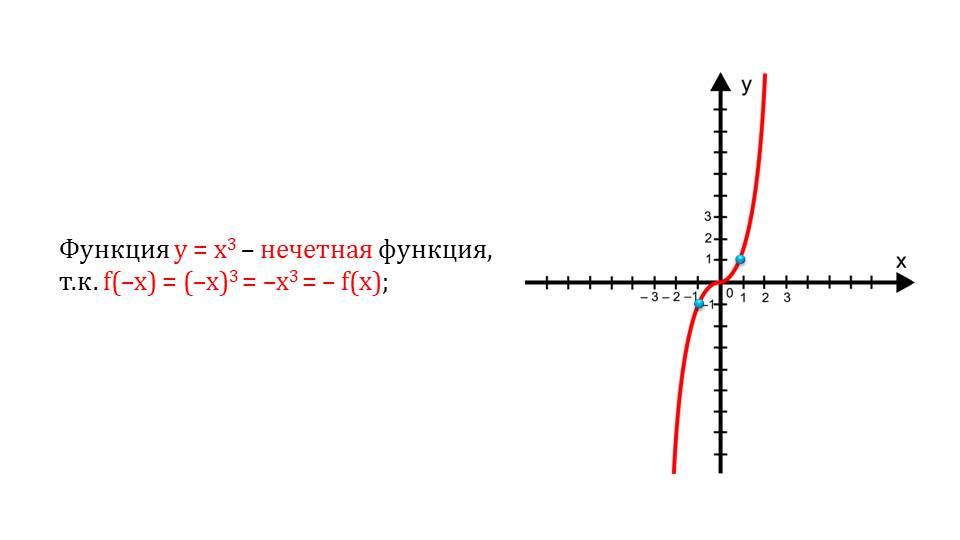
Пятое свойство – четность. Любая функция может быть либо четной, либо нет. Изначально дается определение четности. При равенстве некоторой функции с аргументом от х этой же функции с аргументом –х функция будет являться четной. Приводится пример такой функции, нетрудно догадаться по графику, что это парабола. Можно заметить симметричность относительно ОУ. Аналогичным образом рассматривается нечетность.

И, наконец, последним свойством, которое указывается в данной презентации – это периодичность.
| Автор | |
|---|---|
| Дата добавления | 27.07.2014 |
| Раздел | Алгебра |
| Подраздел | Презентация |
| Просмотров | 3016 |
| Номер материала | 778 |