
Презентация "Тангенс суммы и разности аргументов"

Краткое описание документа:
Презентация «Тангенс суммы и разности аргументов» является наглядным пособием для сопровождения объяснения учителя по данной теме. В ходе демонстрации представляются формулы преобразования, представляющие собой тангенс разности или суммы аргументов в сумму или разность произведений косинусов и синусов аргументов, приводятся примеры решения заданий разной сложности с использованием данных формул. Задача данной презентации – наглядное представление учебного материала таким образом, чтобы он лучше запоминался, легче усваивался учениками.

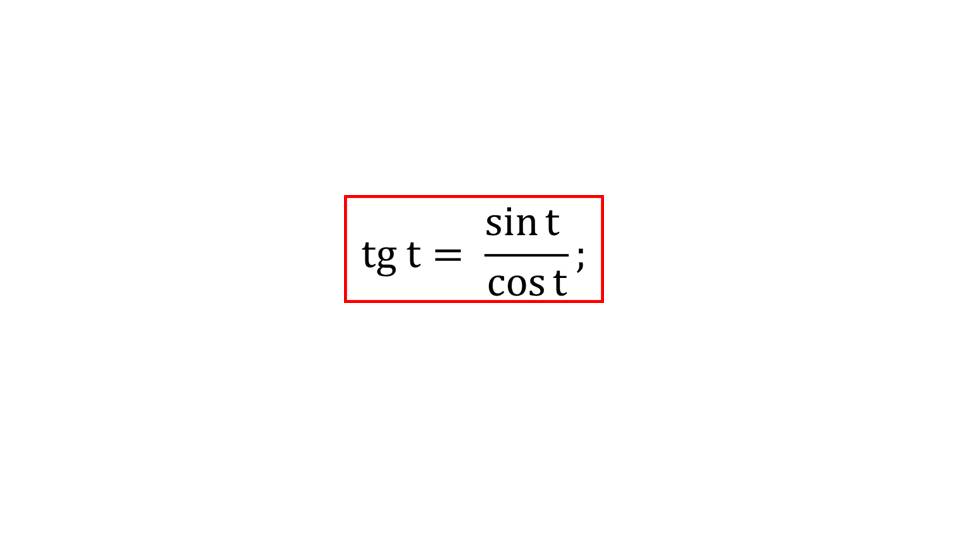
В презентации используются анимационные эффекты, которые улучшают восприятие материала, удерживают внимание ученика на изучаемом предмете. Формулы, которые необходимо запомнить ученику, выделяются с помощью яркой рамки. Примеры, решение которых описывается, дополняются таблицами основных значений синусов и косинусов, необходимых для решения задач. Ученикам не нужно пользоваться дополнительными материалами для освоения темы.
Демонстрация начинается с напоминания формул, изученных на прошлых уроках – синуса, а также косинуса суммы аргументов. Также ученикам напоминается, что тангенсом угла является отношение его синуса к косинусу tg t=sin t/cos t. На третьем слайде демонстрируется выведение формулы тангенса суммы.

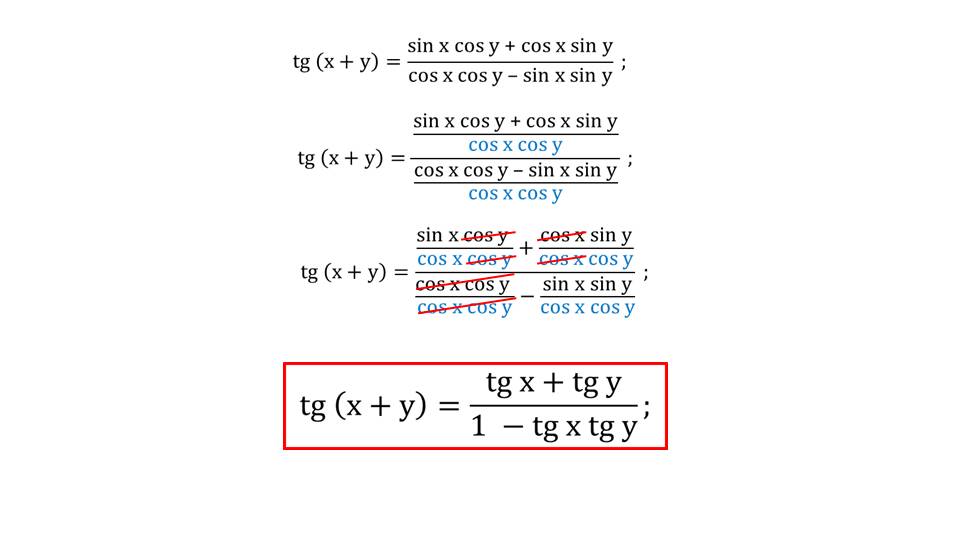
Для этого в формулу тангенса суммы подставляются формулы синуса суммы двух аргументов и косинуса данной суммы. После подстановки в отношение правой части формул, представляющих синус и косинус сложенных аргументов в виде суммы (разности) произведений, получается tg (х+у)= (sin х cos у + cos x sin y)/(cos x cos e – sin x sin y). Чтобы упростить выражение, числитель и знаменатель дроби делятся на выражение cos x cos y. После сокращения одинаковых множителей, дробь преобразуется в вид tg (х+у)= (tg х+ tg у)/(1-tg x tg y).
На слайде 5 без доказательства предлагается к запоминанию формула тангенса разности аргументов tg (х-у)= (tg х- tg у)/(1+tg x tg y). Эта формула выводится аналогично предыдущей, и при желании ученики могут вывести ее самостоятельно.
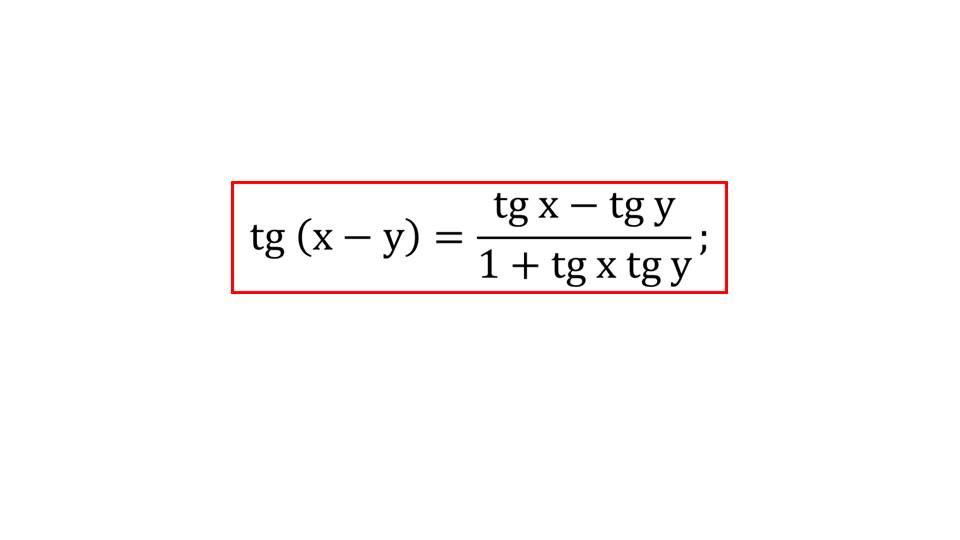
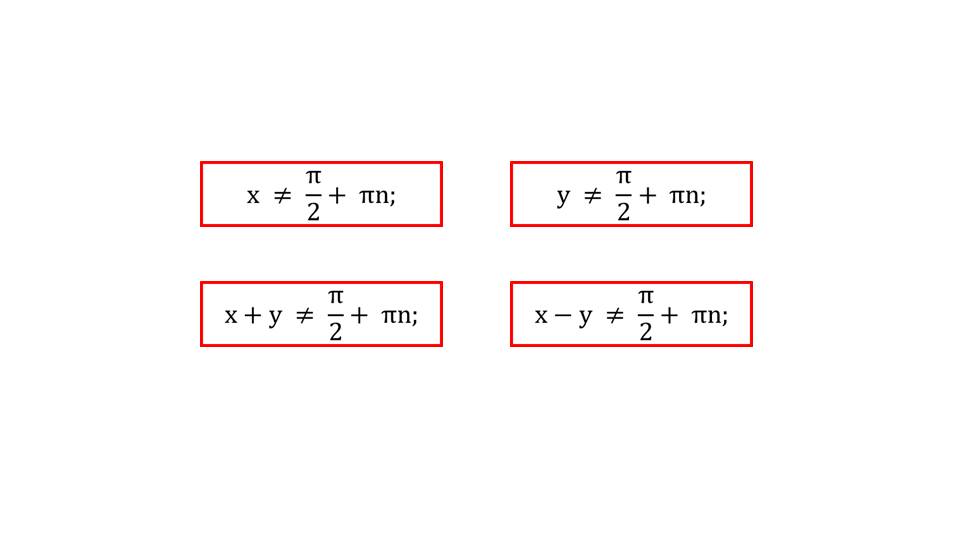
У формул тангенса суммы и разности аргументов есть особенность, которую обязательно нужно запомнить. На экран выведены в рамке ограничения, которые накладываются на применение формулы. Она не имеет смысла для значений х, при которых знаменатель дроби обращается в нуль. Поэтому х≠π/2+πn, у≠ π/2+πn, х+у≠π/2+πn, х-у≠ π/2+πn.
В первом примере требуется вычислить значение дроби, вид которой напоминает правую часть изученной формулы тангенса суммы аргументов. Нужно найти значение (tg 16°- tg 44°)/(1+tg 16° tg 44°). Применив формулу тангенса суммы аргументов, получаем упрощенное выражение tg (16°+44°), что равно tg 60°=√3. Таким образом, решение задания свелось к упрощению выражения и вычислению обычного табличного значения тангенса.


Во втором примере нужно упростить выражение, часть которого представляет собой тангенс суммы аргументов и тангенс разности аргументов ((tg х+ tg у)/tg (x+y))+ ((tg х-tg у)/tg (x-y)). Чтобы упростить выражение, знаменатели обеих дробей преобразуем с помощью изученных формул тангенса суммы и разности. Напоминание о виде формул выведено на экран, чтобы ученикам было легче усвоить ход рассуждений при решении и запомнить формулы. После подстановки правой части формул вместо соответствующих выражений в знаменателях получается сумма отношений, в которых числитель изнаменатель сокращаются, оставив в результате выражение 1-tg x tg y + 1 + tg x tg y. После сокращения подобных слагаемых, получаем значение выражения, равное 2.
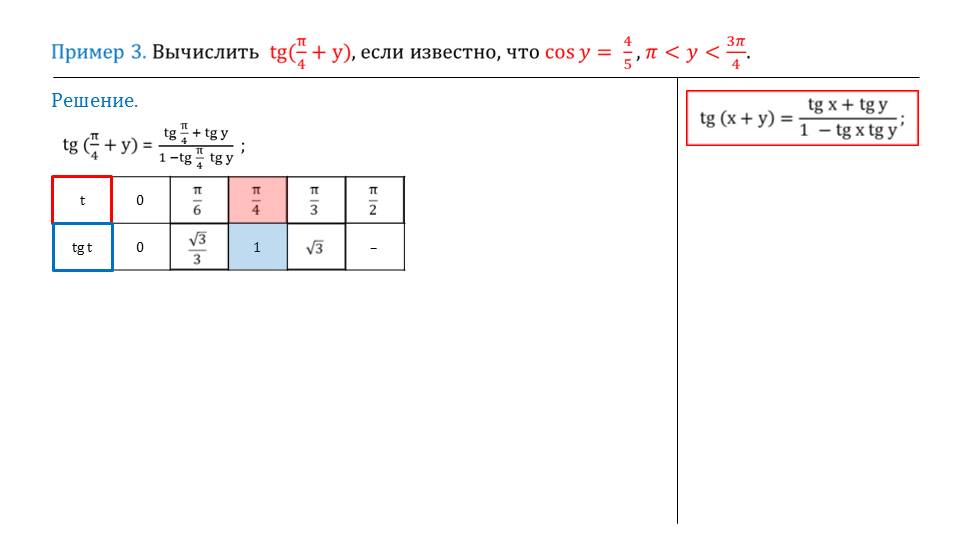

Третий пример описывает вычисление выражения tg(π/4+y), в котором известно, что cos y=4/5, а на у наложено ограничение π<y<3π/4. Исходное выражение представляет собой тангенс суммы аргументов. После применения к нему формулы преобразования, получается выражение tg(π/4+y)=(1-tg π/4 tg y). Из таблицы тангенсов берем соответствующее значение tg π/4=1. После подстановки значения тангенса получаем tg(π/4+y)=(1+tg y)/(1-tg y). Чтобы вычислить значение выражения потребуется также вспомнить основное тригонометрическое тождество, из которого следует справедливость формулы 1+tg2 y=1/cos2y. Зная, что cos y=4/5, определяем tg2 y=1/cos2y-1=25/16-1=9/16.
Соответственно, значение tg y=3/4 и tg y=-3/4. Учитывая ограничение на у подставляем подходящее значение в исходную формулу и получаем tg(π/4+y)=(1+3/4)/(1-3/4). Вычислив значение выражения, находим ответ tg(π/4+y)=7.
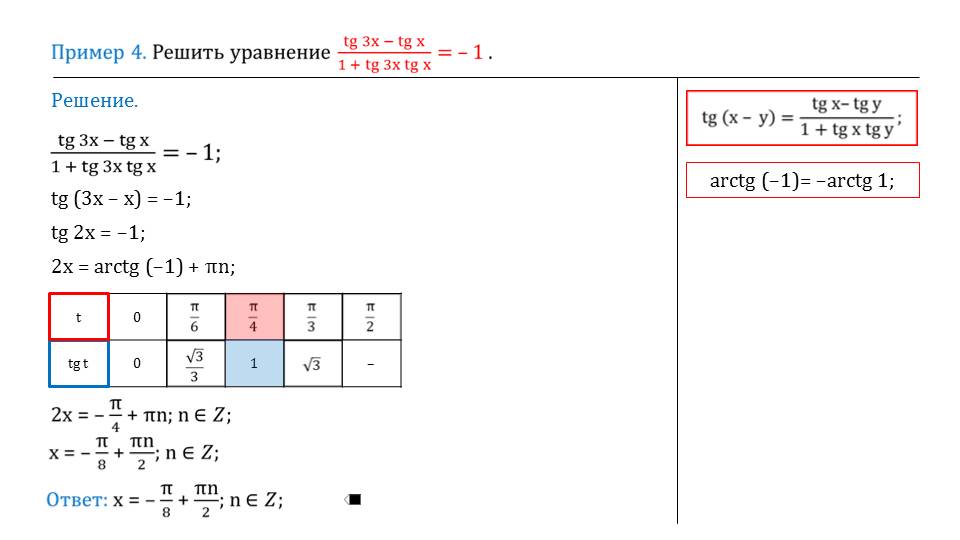
В последнем примере необходимо решить уравнение (tg 3x-tg x)/(1 + tg 3x tg x)=-1. Очевидно, левая часть уравнения напоминает правую часть формулы тангенса разности аргументов (tg х- tg у)/(1+tg x tg y). После преобразования получим из нее tg(3x-x)=-1, то есть tg 2x=-1. Из этого простого уравнения легко найти 2х=arctg(-1)+πn. Для преобразования выражения также используем формулу arctg(-1)=-arctg1. Из таблицы значений тангенсов видно, что такие значения справедливы для угла π/4. Поэтому 2х=-π/4+πn для любых целых n. Отсюда значение корня х=-π/8+πn/2 для любых целых n. Решение уравнения найдено.
Презентация «Тангенс суммы и разности аргументов» поможет повысить эффективность урока алгебры за счет обеспечения хорошего наглядного представления учебного материала. Также презентация будет полезна учителям, подбирающим инструменты для дистанционного обучения. Детально разобранное решение примеров, описанных в презентации, поможет ученикам понять особенности решения задач различной сложности.
| Автор | |
|---|---|
| Дата добавления | 27.07.2014 |
| Раздел | Алгебра |
| Подраздел | Презентация |
| Просмотров | 4782 |
| Номер материала | 798 |