
Презентация "Теорема о трёх перпендикулярах"

Краткое описание документа:
Презентация «Теорема о трёх перпендикулярах» демонстрирует наглядный учебный материал для освоения данной темы. В ходе презентации формируется понятие о предмете теоремы, представляется формулировка теоремы и обратной к ней, а также демонстрируются доказательства. Более глубокое понимание и лучшее усвоение материала достигается с помощью рассмотрения примеров решения задач с использованием полученных теоретических знаний. Используя презентационный материал, учитель может повысить эффективность урока, преподнести ученикам материал в виде, наиболее выгодном для понимания.
Использование в презентации анимационных эффектов дает преимущество данному средству наглядности перед другими средствами. Анимация делает демонстрацию более живой, похожей на традиционное представление с помощью доски и мела. Однако при этом все сделанные построение имеют четкое изображение, есть возможность выделить важные детали, особенности, преобразования геометрических объектов, их взаимное расположение не только на плоскости, но и в пространстве. Определения и формулировки теорем легче запоминаются, если они не только произнесены учителем, но и представлены на экране, выделив понятие ярким цветом, сопровождая его соответствующими построениями.
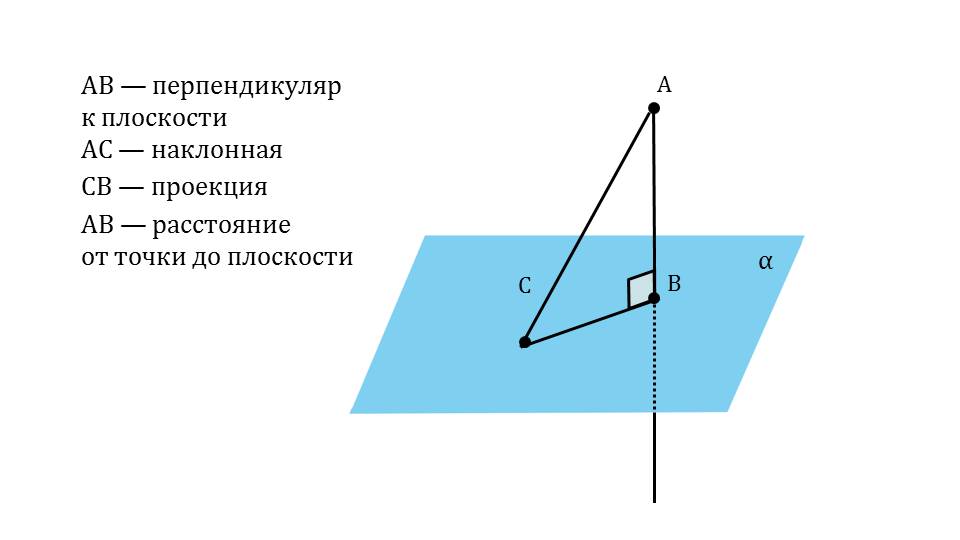
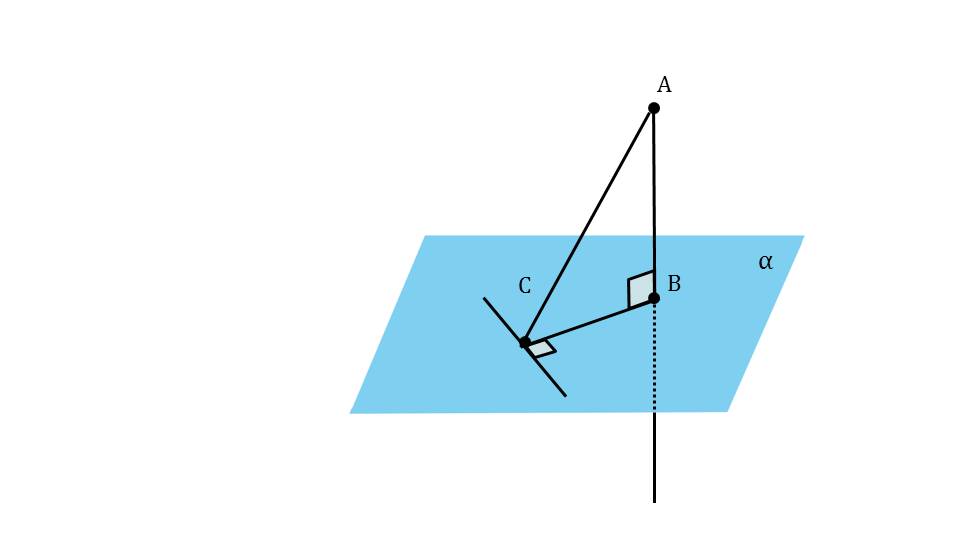
Условие теоремы демонстрируется с помощью построения, на котором хорошо видно особенности условия теоремы. На рисунке изображается плоскость α и не принадлежащая ей точка А. от А к плоскости опускается перпендикуляр АВ. К отмеченной на плоскости некоторой точке С опускается также наклонная из точки А, образуя отрезок АС. Отрезок, соединяющий основание перпендикуляра В и точку С является проекцией наклонной АС. Перпендикуляр АВ представляет отрезок, длина которого определяет расстояние от точки А до плоскости α. В точке С достраивается прямая, перпендикулярная к отрезку ВС – проекции наклонной.

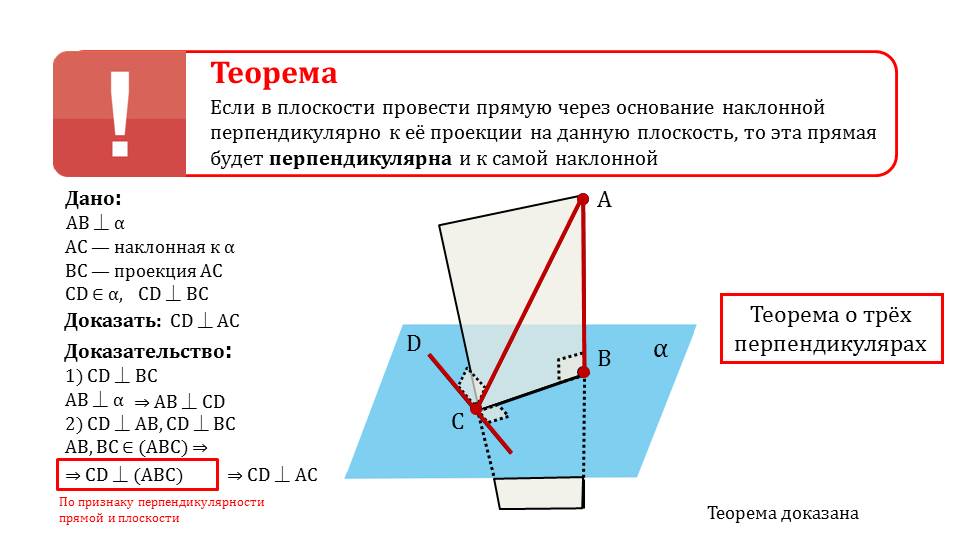
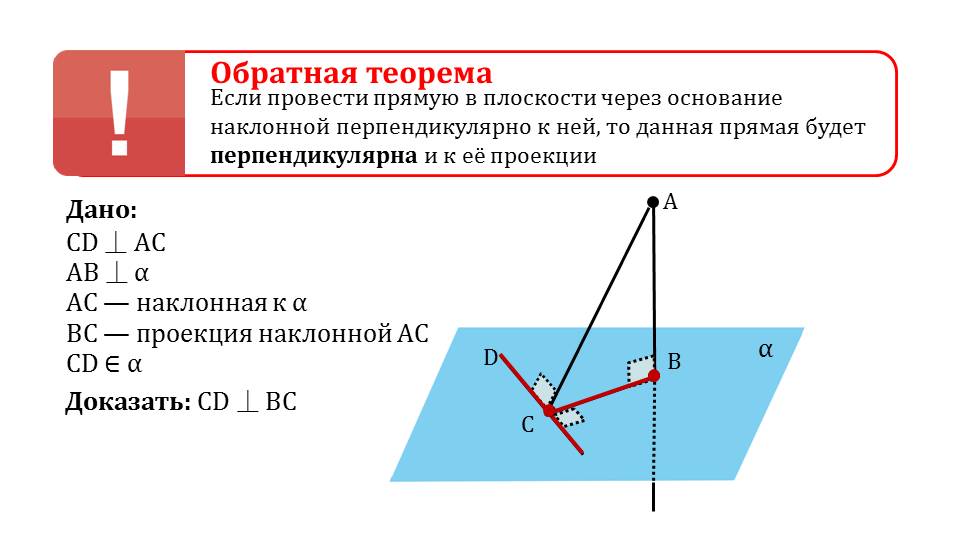
На следующем слайде представлена теорема, в которой указано, что при проведении в плоскости перпендикулярной к проекции наклонной прямой через точку основания, прямая оказывается перпендикулярной к наклонной. Далее представлено доказательство теоремы. На рисунке выделяются основные объекты рассмотрения – наклонная АС, перпендикуляр АВ, прямая CD, принадлежащая плоскости α, перпендикулярная проекции ВС. Рядом с рисунком отмечено, что иначе данная теорема в геометрии называется теоремой о трех перпендикулярах. Необходимо доказать перпендикулярность CD и АС. Зная о перпендикулярности прямой CD проекции ВС и перпендикулярность перпендикуляра АВ плоскости α, можного говорить о перпендикулярности перпендикуляра и проведенной прямой CD. Учитывая этот факт, а также перпендикулярность CD проекции и то, что АВ и Вс принадлежат одной плоскости (АВС), можно говорить о перпендикулярности CD и плоскости (АВС) по признаку перпендикулярности прямой и плоскости. А так как наклонная принадлежит плоскости (АВС), то CD перпендикулярна наклонной АС. Также верна обратная теорема о том, что если через основание наклонной проведена перпендикулярная к ней прямая, то эта прямая также будет перпендикулярна к проекции наклонной.

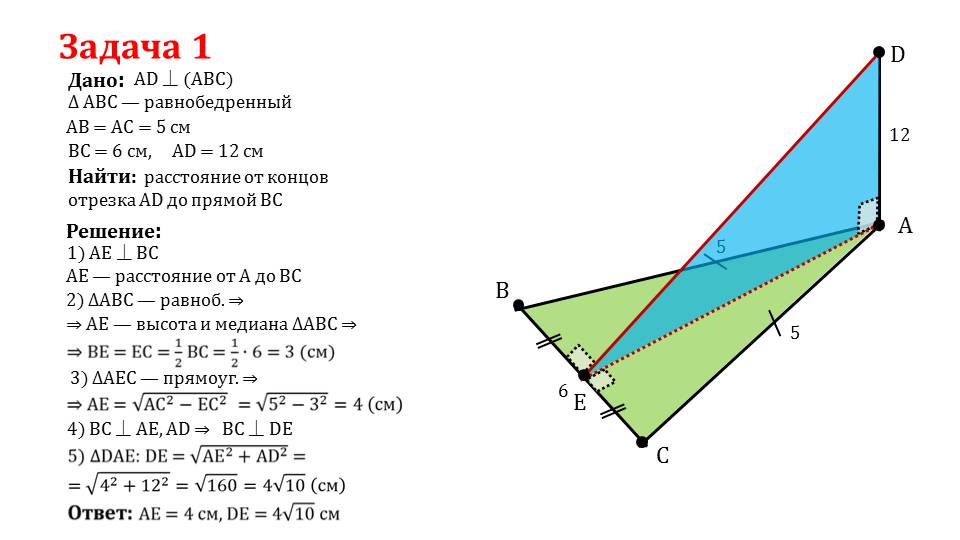
Рассматривается описание решения задачи, в которой необходимо найти расстояние от концов отрезка АD до прямой ВС. Условие задачи включает имеющийся на плоскости равнобедренный треугольник ΔАВС, перпендикулярно к этой плоскости проведенный отрезок АD. Известны расстояния АВ=АС=5 см, ВС=6 см, АD=12 см. чтобы решить задачу, из А опускается перпендикуляр в треугольнике ΔАВС на основание ВС, который представляет расстояние от А до ВС. Из равнобедренности треугольника следует, что АЕ – это высота и медиана. При этом ВЕ=ЕС=1/2ВС=3 см. Из того, что треугольник ΔАЕС является прямоугольным, следует, что АЕ=√(АС2-ЕС2)=√52-32)=4 см. Из перпендикулярности ВС к АЕ и АD следует перпендикулярность ВС и DЕ. А свойства прямоугольного треугольника Δ DАЕ позволяют найти DЕ=√(АЕ2- АD 2)=√42-122)=4√10 см. Задача решена.
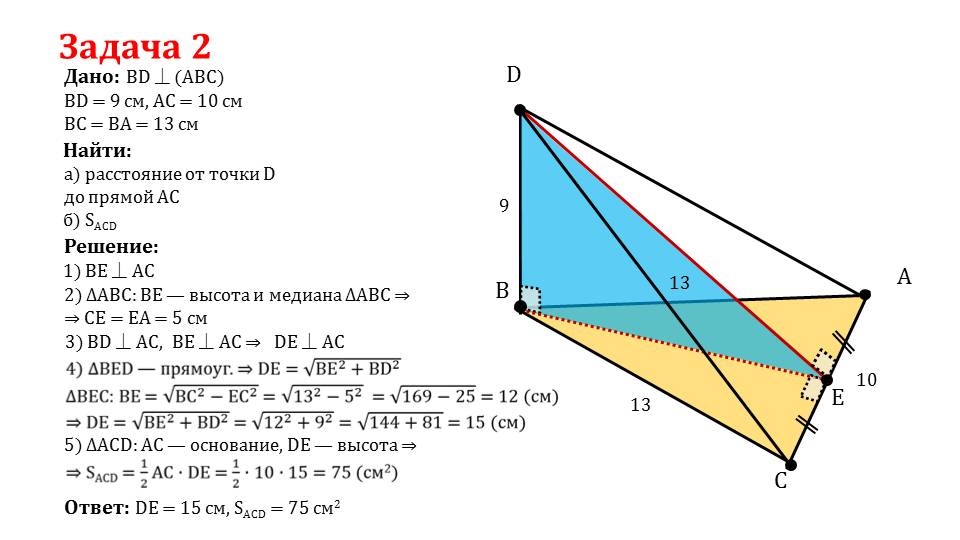
Во второй задаче необходимо найти расстояние от точки, отмеченной вне плоскости, до прямой, принадлежащей плоскости и площадь треугольника. Дан равнобедренный треугольник. К плоскости, на которой лежит треугольник проведена в его вершине В перпендикулярная прямая на расстоянии ВD=9 см. Основание треугольника АС=10 см, а стороны ВС=ВА=13 см. Чтобы решить задачу, строится высота равнобедренного треугольника ΔАВС. Из ее свойств следует равенство частей, на которые разбивается основание АС точкой Е – СЕ=ЕА=5 см. так как две стороны треугольника ΔВDЕ перпендикулярны стороне АС, то третья сторона DЕ также перпендикулярна АС. Для прямоугольного треугольника ΔВDЕ верно равенство DЕ=√(ВЕ2+ ВD2), а для треугольника ΔВЕС верно ВЕ=√(ВС2-ЕС2)=√(169-25)=12 см. теперь можно найти DЕ=√(144+81)=15 см. Зная величину основания треугольника и его высоты, находим площадь S=(1/2)АС·DЕ=75 см. Задача решена.
Презентация «Теорема о трёх перпендикулярах» рекомендована к применению на уроке геометрии в школе для повышения его эффективности. Также данный материал может с успехом использоваться в ходе дистанционного обучения. Материал может быть рекомендован к самостоятельному рассмотрению учениками, которым требуется дополнительное занятие для более глубокого усвоения материала.
| Автор | |
|---|---|
| Дата добавления | 28.10.2014 |
| Раздел | Геометрия |
| Подраздел | Презентация |
| Просмотров | 10904 |
| Номер материала | 892 |