
Презентация "Уравнение касательной к графику функции"

Краткое описание документа:
Презентация «Уравнение касательной к графику функции» является наглядным пособием, помогающим освоить умение составлять уравнение касательной к графику функции в заданной точке, а также применять эти знания в решении других задач. Когда вводилось понятие производной, был раскрыт ее геометрический смысл. Понимание связи производной функции в точке и касательной, построенной в данной точке, позволяет решить множество задач, поэтому наглядное пособие построено так, чтобы достичь глубокого понимания данной связи, научить учеником использовать это знание в решении задач.
Форма презентации – наиболее удобная форма представления данного материала, так как презентация предоставляет широкий набор инструментов для формирования объяснения. Анимированное представление графиков и построений помогает отследить преобразования, подметить важные детали.
Данная тема содержит много рисунков, а при помощи средств презентации такие рисунке наиболее корректно и наглядно можно представить только в электронном виде.
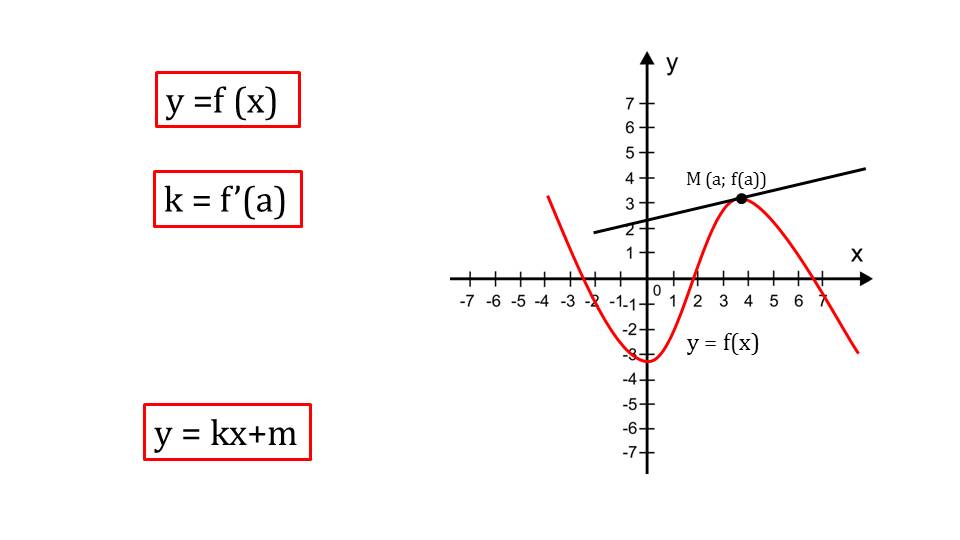
Презентация начинается с построения на координатной плоскости графика некоторой функции у=f(x). Ставится задача - необходимо построить касательную к графику функции в некоторой заданной точке с координатами М(а, f(а)). Так как касательная является прямой линией, ее график определяется уравнением y=kx+m. Коэффициент уравнения находится посредством нахождения производной функции в данной точке k=f΄(a).
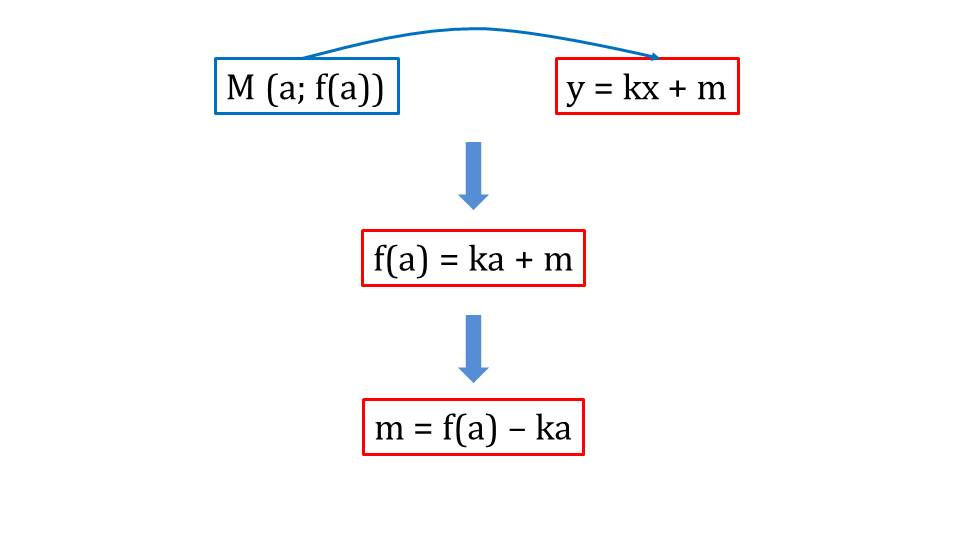
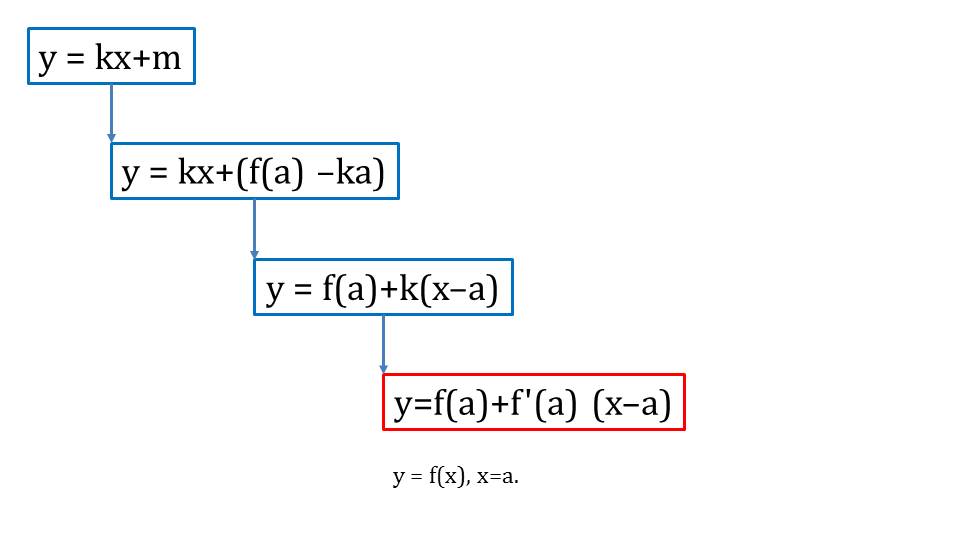
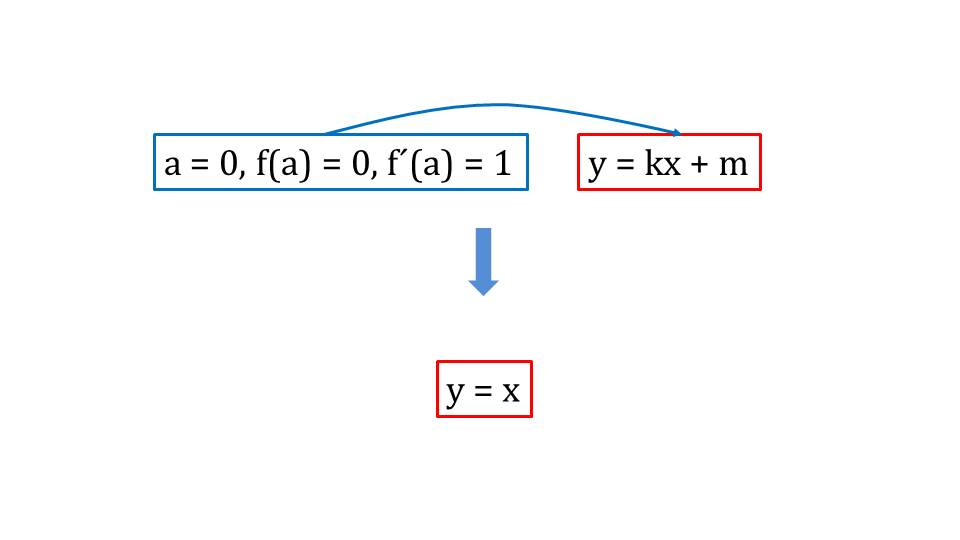
На слайде 2 схематично отображена связь между координатами точки касания и уравнением касательной. Отмечается, что используя данную связь можно найти недостающий коэффициент m. Так как значение функции в данной точке равно значению уравнения касательной при подстановке коэффициента к и координаты точки. Отсюда m= f(а)- ka. Пошагово подставив все отмеченные выражения для нахождения неизвестных, получаем общее представление формулы для нахождения у= f(а)+ f΄(a)(х-а).

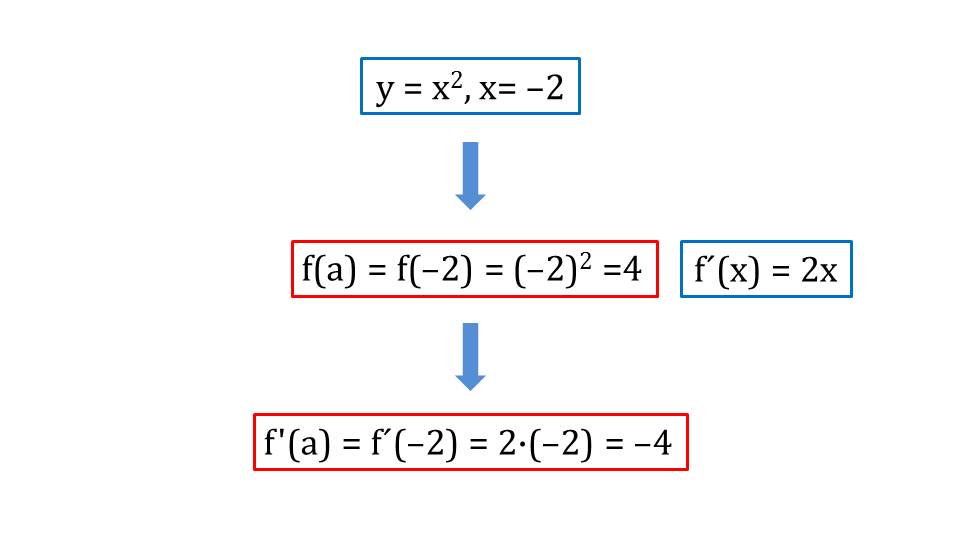
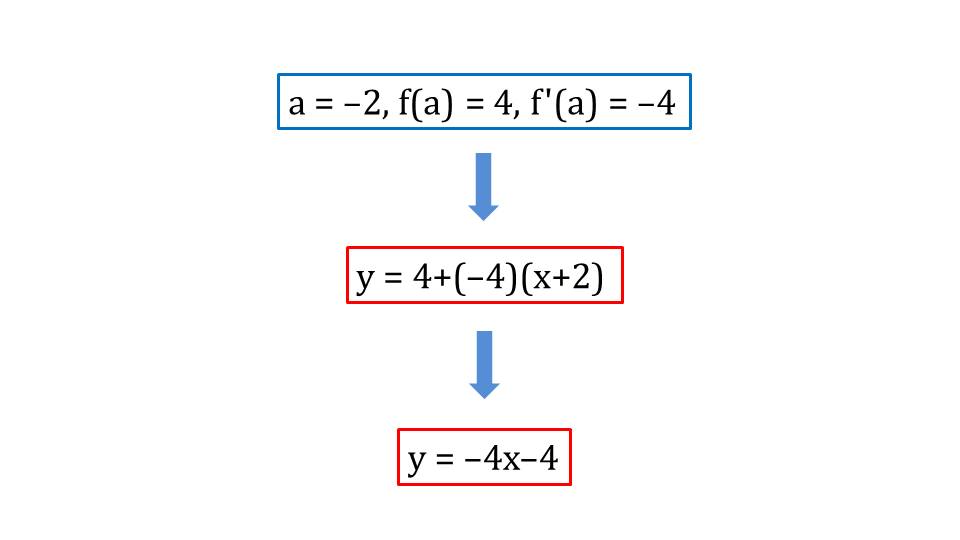
Согласно данной схеме находится уравнение касательной функции у=х2 в х=-2 на слайде 4. Вычислив f(а)=4 и зная, что f΄(х)=2х, определяем значение производной в данной точке f΄(a)=-4. Подставив полученные значения а=2, f(а)=4 и f΄(a)=-4 в общий вид уравнения касательной, получаем у=4+(-4)(х+2) или у=-4х-4.
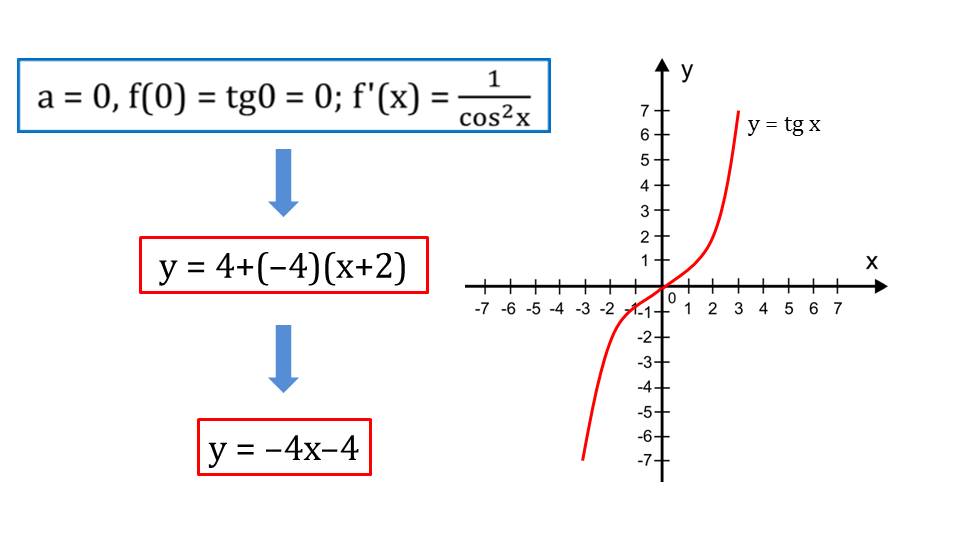
На слайде 6 приведен пример функции у=tgx. Находим основные параметры для составления уравнения касательной в заданной точке. При а =0, значение f(0)=0 и f΄(х)=1/cos2x. При этом f΄(0)=1 Подставив найденные значения в формулу общего вида касательной, получаем у=х.


После рассмотрения процесса составления уравнения касательной к графику функции в заданной точке, выведено общее правило его составления в виде алгоритма действий. Отмечается, что для составления уравнения касательной к графику у= f(х) нужно обозначить а - абсциссу точки касания, вычислить значение функции в ней f(а), найти производную функции f΄(х) и ее значение в точке f΄(a). А затем остается подставить полученные значения в формулу.
Далее рассматривается решение примеров, в которых нужно составить уравнение касательной. В примере 1 требуется составить такое уравнение для функции у=-1/δ в х=1. Задание решается по известному алгоритму. Фиксируется а=1, находится f(a)= f(1)=1. Производная f΄(х)=1/δ2, а ее значение в а будет f΄(a)=1. Соответственно, уравнение касательной в данной точке после подстановки значений и преобразования получает вид у=х-2.
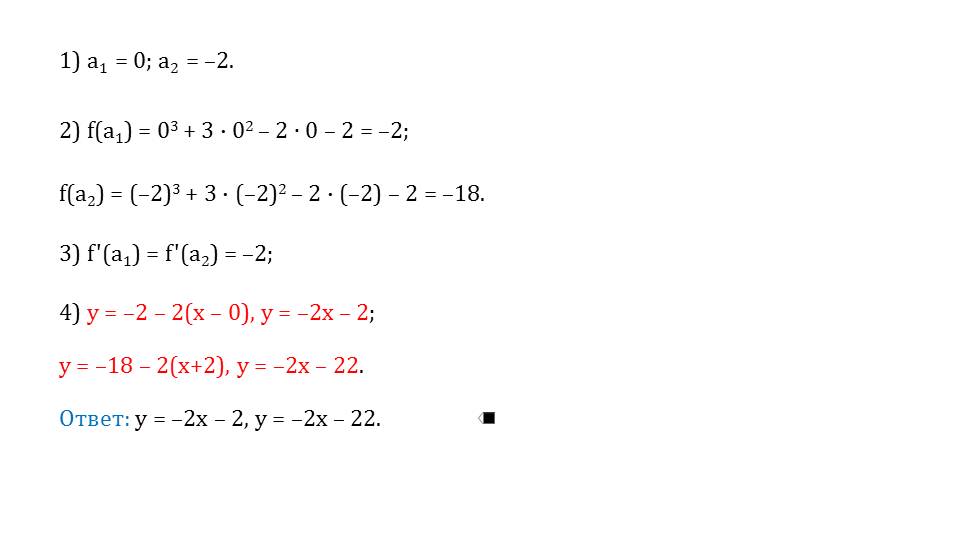

Пример 2 рассматривает более сложное задание, в котором нужно найти уравнение касательной к графику у=х3+3х2-2х-2, параллельной к прямой у=-2х+1. Так как параллельные прямые будут иметь одинаковый коэффициент k, отмечается, что k=-2, в то время как f΄(a)=-2. Производная функции будет f΄(х)=3х2+6х-2, а f΄(а)=3а2+6а-2. Если производная в точке а равна -2, то 3а2+6а-2=-2. Корнями уравнения будут а1=0 и а2=-2. Значения функции в этих точках f(a1)=-2, f(a2)=-18. При этом f΄(a1)= f΄(a2)=-2. Получаем два уравнения касательной у=-2х-2 и у=-2х-22.
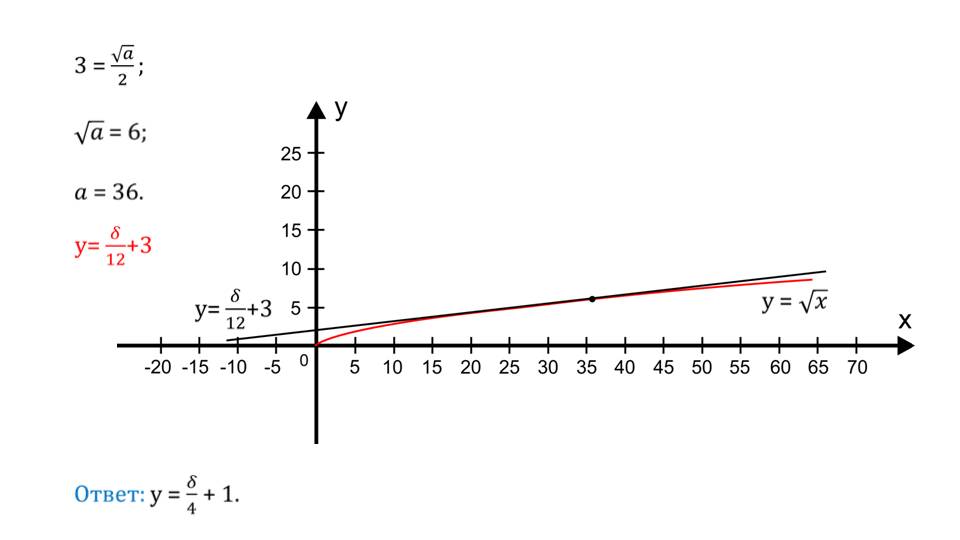
В примере 3 требуется построить касательную к функции у=√δ в точке (0,3). Согласно известному алгоритму выполняется ряд действий, в результате которых получаем уравнение касательной у=δ/(2√а)+√а/2. После подстановки соответствующих координат точки касания получаем уравнение касательной у=δ/12+3. На рисунке демонстрируется построение графика исходной функции и касательной ее в точке (0,3).

На слайде 14 напоминается информация о приращении значения функции и его вычислении для приращения аргумента. На последнем слайде описано решение примера, в котором требуется найти приближенное значение числового выражения 2,0036. При решении примера определяем, что у=х7, а х=2,003. При этом f(х)=х6, а=2, f(а)= f(2)=64. Для х=2,003 f(х)=6х5 и f(а)=192. Чтобы найти приближенное значение, остается произвести вычисления 2,0036≈65-192·0,003. Получаем значение 2,0036≈64,576.

Презентация «Уравнение касательной к графику функции» рекомендуется применять на уроке в школе. Также материала полезен для проведения уроков дистанционного обучения, может пригодиться для самостоятельной работы ученикам, которым нужно более глубоко усвоить материал.
| Автор | |
|---|---|
| Дата добавления | 27.07.2014 |
| Раздел | Алгебра |
| Подраздел | Презентация |
| Просмотров | 5353 |
| Номер материала | 820 |