
Презентация "Вычисление производных"

Краткое описание документа:
Презентация «Вычисление производных» является наглядным пособием, сопровождающим объяснение учителя по данной теме урока. В ходе презентации ученикам дается учебный материал, необходимый для освоения умения находить производную функции – необходимые определения и понятия, формулы для вычисления производных основных видов функций, свойства производной.

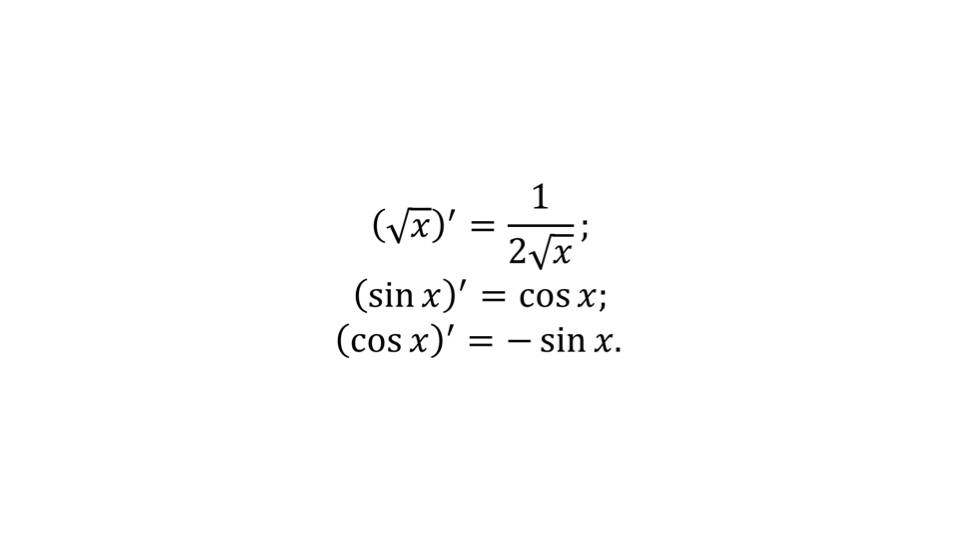
С помощью данной презентации учитель имеет возможность наглядно представить материал, сложный для понимания, способствовать лучшему запоминанию правил и формул.


Представление информации в форме презентации имеет много преимуществ. Она является средством, вносящим разнообразие в ведение урока для удержания внимания учеников на изучении предмета. Использование анимации в составлении наглядного пособия дает возможность подавать материал таким образом, чтобы он был более понятным ученикам. Использования ярких цветов и других способов выделения текста, формул и деталей построений способствует лучшему пониманию и запоминанию материала.


Презентация начинается с определения формул дифференцирования. Так называются формулы, помогающие отыскать производные функций. В качестве примеров нахождения производных различных функций приводятся С΄=0, х΄=1, (kx+m)΄=k, (x2)΄=2х, (x3)΄=3х2, (1/х)΄=-1/х2. На слайде 2 также продемонстрировано нахождение производных (√х)΄=1/2√х, (sinx)΄=cosx, (cosx)΄=-sinx.

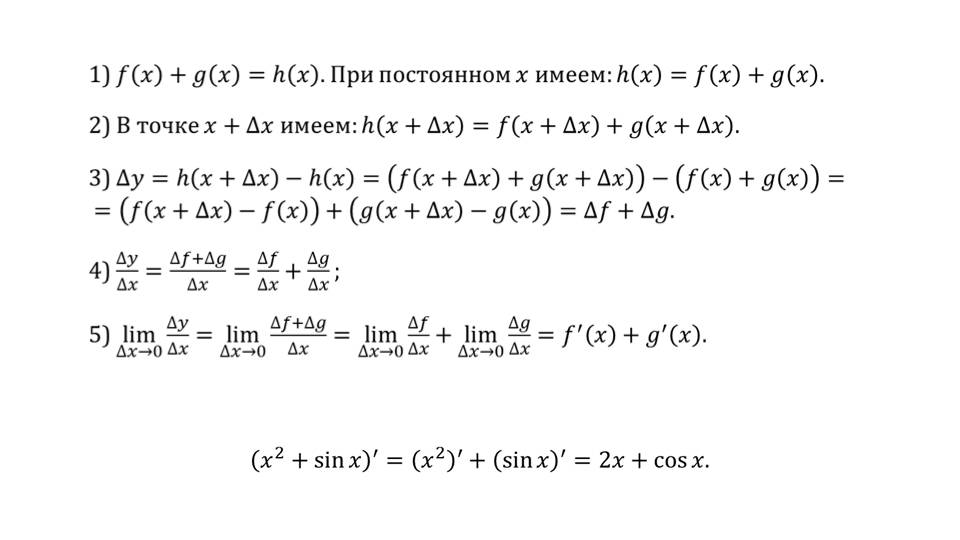
При решении примера 1 рассматривается нахождение производных функций, среди которых встречаются линейные, степенные, дробные, тригонометрические выражения. В условии предлагается найти производные 6 функций в заданных точках. В результате применения известных способов нахождения производных определяется их значение: а) (-2х+7)΄=-2, f΄(√5)=-2, б) (х2)΄=2х, f΄(-2)=-4, в) (1/х)΄=-1/х2, f΄(1/3)=-9, г) (√х)΄=1/2√х, f΄(9)=1/6, д) (sinx)΄=cosx, f΄(π)=-1, е) (cosx)΄=sinx, f΄(π/4)=-√2/2.


В примере 2 необходимо составить уравнение касательной к графику функции у=х2 в точке х=-1. В начале решения напоминается, что касательная является прямой, уравнение которой линейное у=kx+m. При этом коэффициент k= f΄(-1). Производная функции (х2)΄=2х, а в точке х=-1 f΄(-1)=-2. Получаем уравнение у=-2х+m. Так как касательная строится в точке (-1,1),при подстановке значений в уравнение касательной 1=(-2)·(-1)+mможно найти значение m. Отсюда m=-1. Уравнение касательной у=-2х-1.


Далее находится производная у=√х по известному алгоритму. Отмечается, что для фиксированного х>0 f(x)=√x. В точке x+Δх значение функции f(x+Δх)=√( x+Δх), а приращение функции равно Δу=f(x+Δх)-f(x)=√(x+Δх)-√x. При этом отношение приращений Δу/ Δх= 1/(√(x+Δх)+√х), а его предел limΔу/Δх= 1/2√х при Δх→0. Соответственно, (√х)΄= 1/2√х.


На слайде 6 описывается нахождение производной у=sinx. В ходе анализа согласно известному алгоритму поиска производной получаем (sinx)΄=cosx.
Далее ученикам демонстрируется правило нахождения производной суммы. Отмечается, что для f(x) и g(x), имеющих производную в точке х верно утверждение, что в этой точке есть производная и их суммы, при этом верно равенство (f(x)+ g(x))΄= f΄(x)+ g΄(x). На слайде 8 доказывается справедливость данного равенства с использованием известного алгоритма поиска производной функции, а также приводится пример использования изученного правила (х2+sinx)΄=( х2)΄+( sinx) ΄=2x+cosx.


Правило 2 на слайде 9 отмечает справедливость утверждения о том, что если существует производная у= f(x), то для у= kf(x) также существует производная. При этом (kf(x))΄=kf΄(x). Справедливость данного утверждения доказывается по известному алгоритму поиска производной на слайде 10, а также приводятся примеры нахождения производной с использованием правила – (5х2)΄=5(х2)΄=5·2х=10х, (-cosx/3)΄=-1/3(cosx)΄=1/3sinx.


На слайде 11 демонстрируется правило 3, в котором определяется свойство производной произведения функций f(x) и g(x), которые имеют производные в точке х. отмечается, что произведение таких функций также имеет в этой точке производную, вычисляемую по формуле (f(x)g(x))΄= f΄(x)g(x)+ f(x)g΄(x). Ниже приводится пример применения правила ((2x+3)sinx)΄=(2x+3) ΄sinx + (2x+3)(sinx) ΄=2sinx + (2х+ 3) cosx.
Далее представлено правило 4 о нахождении производной частного. Отмечается, что для f(x) и g(x), имеющих производную в точке х справедливо, что частное f(x)/ g(x) также имеет производную в х. при этом g(x)≠0, а (f(x)/ g(x)) ΄= (f΄(x)g(x)- f(x)g΄(x))/ g2(x). Ниже описывается решение примера с использованием правила (х2/(5-4х))΄. После подстановки значений в формулу и проведения вычислений получаем (х2/(5-4х))΄=(10х-4х2)/(5-4х)2.
Для закрепления изученного материала и формирования умения применять правила при решении заданий, рассматривается ряд примеров.
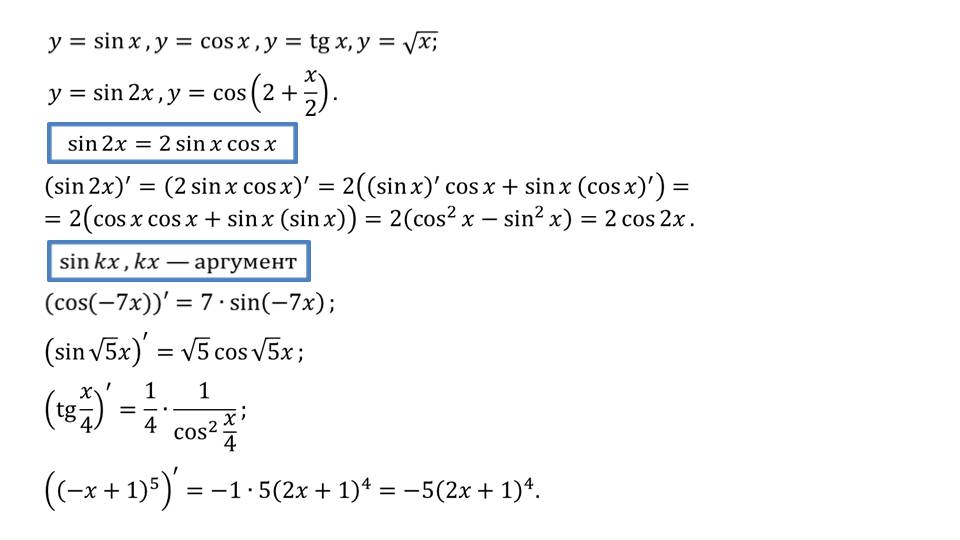
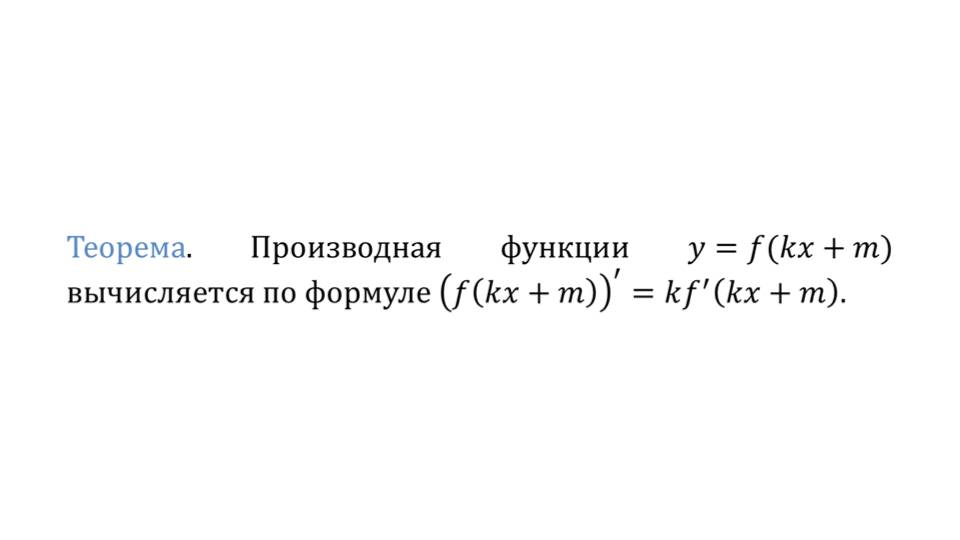
В примере 3 требуется найти производную у=3х2-4х+2. После применения формулы производной суммы и вычислений получаем ответ у΄=6х-4. В примере 4 нужно найти производные функций у=х4 и у=х5. Применяя правило нахождения производной произведения, находим (х4) ΄=4х3, а (х5)΄=5х4. На основе полученных результатов делается предположение, что (хn)΄=nxn-1. При решении примера 5, где требуется найти точки графика у=х3-3х+2, в которых касательная параллельна оси х. при решении находится у΄=3х2-3. Полученное выражение приравниваем нулю, находим из него х1=1 и х2=-1. В данных точках ищем значение функции. Получаем ответ, что точки, удовлетворяющие условию – (1, 0) и (-1, 4).
На слайдах 16 и 17 демонстрируется нахождение производной функций tgxи ctgx. Выразив данные функции через синус и косинус, получается отношение, для поиска производной которого используется правило поиска производной частного. После проведения преобразований получим (tgx)΄=1/cos2x и (сtgx)΄=1/sin2x.
На слайде 18 приводится пример решения обратной задачи – при известной производной нужно найти саму функцию. Примерами служат f΄(x)=cosx, где f(x)= sinx, а также f΄(x)= x3, где f(x)=x4/4.
Далее, на слайде 19, приводятся примеры нахождения производной ряда функций, в решении которых используются различные преобразования и изученные правила.

В конце презентации представлена теорема о производной функции у=f(kx+m), где утверждается, что для ее вычисления следует использовать формулу (f(kx+m))΄= kf΄(kx+m). Применение данной формулы при решении задач продемонстрировано на слайде 21 при нахождении значения производной f(x)=√(8-1,15х) в точке 5.
Презентация «Вычисление производных» создана для повышения эффективности традиционного урока математики. Также данный материал может стать полезным инструментом дистанционного обучения. Пособие может быть рекомендовано ученикам, самостоятельно осваивающим предмет или требующим дополнительных занятий.
| Автор | |
|---|---|
| Дата добавления | 27.07.2014 |
| Раздел | Алгебра |
| Подраздел | Презентация |
| Просмотров | 7993 |
| Номер материала | 819 |