
Урок "Арккосинус. Решение уравнения cost = а"

Краткое описание документа:
В продолжение предыдущей темы, в которой рассматривались примеры решения тригонометрических функций, этот видеоурок знакомит учащихся с арккосинусом и решением уравнения cos t = a.
Рассматривается пример решения уравнения cos t =1/4 . Используя числовую окружность, находим точки с координатой х = 1/4, на графике отметим эти точки как M(t1) и N(t2).
На графике видно, что t1 – это длина АМ, а t2 – это длина AN. По-другому можно сказать, что t1 = arccos 1/4; t2 = – arccos 1/4. Решение уравнения t = ± arccos ¼ + 2πk.
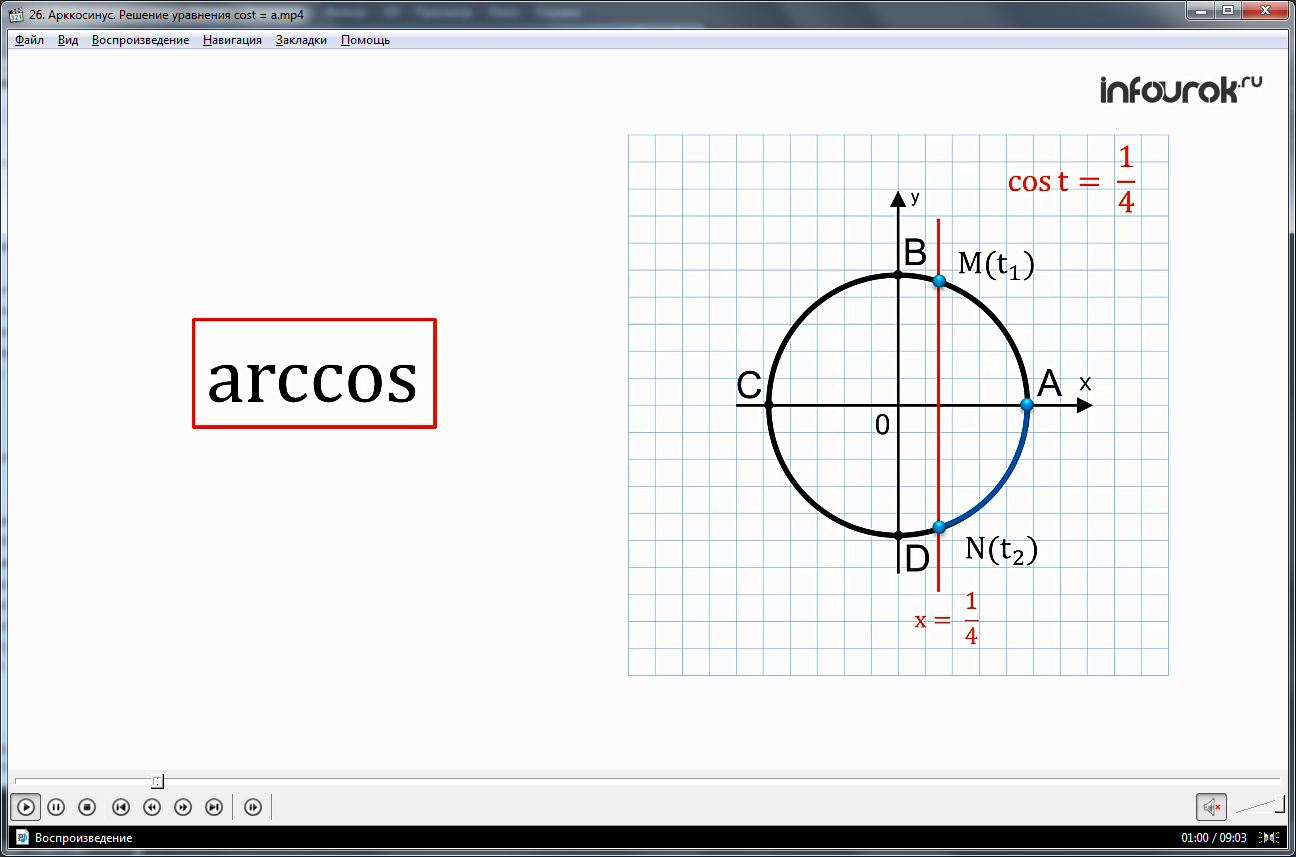
Таким образом, arccos 1/4– это число (длина АМ), косинус которого равен 1/4. Это число принадлежит отрезку от 0 до π/2, т.е. первой четверти окружности.
Далее рассматривается решение уравнения cos t = - 1/4. По аналогии с предыдущим примером, t = ± arccos (-1/4 + 2πk. Можно сказать, чтоarccos (-1/4 – это число (длина дуги АМ), косинус которого равен – ¼ и это число принадлежит II четвертиокружности, т.е. отрезкуот π/2 до π.
Исходя из двух примеров, дается определение арккосинусу: если модуль а меньше или равен 1, то arccos а это такое число из отрезка от 0 до π, косинус которого равен а. Тогда выражение cos t = a при модуле а меньше или равно 1 может иметь вид t = ± arccos a + 2πk. Далее указаны значения t при cos t = 0; cos t = 1; cos t = - 1.
Автор приводит пример 1. Найти решение выражения arcсos. Укажем, что данное значение arcсos равно t, следовательно, cos t равен этому значению, где t принадлежит отрезку от 0 до π. Пользуясь таблицей значений, найдем, что cos t соответствует значение t =π/6. Найдем соответствующее значение косинуса, где π/6 принадлежит отрезку от 0 до π.
Мы получили ответ: π/6. Далее автор обращает внимание на то, что arccos - это значение угла, на которое ушла точка М от точки А. Вся рассматриваемая нами окружность равна 2π, т.е. 360°, тогда угол это arccos t = π/6 равен 60°.
Разберем пример 2. Вычислить arcсos отрицательного числа. Допустим, что arcсos этого числа равен, следовательно, cos t равен этому числу, где t принадлежит отрезку от 0 до π. По таблице значений увидим, какое значение соответствует cos t, это t = 5π/6. Т.е. cos 5π/6 это минус корень из трех, деленный на два, где 5π/6 принадлежит отрезку от 0 до π.
Далее автор рассматривает теорему: для любого а, принадлежащего отрезку от минус одного до одного, действительно равенство arccos a + arccos (-a) =π.При доказательстве для определенности считаем, что а > 0, тогда – а < 0. На окружности отметим arccos a, это длина АК, и arccos (- a), это длина TС. АК = ТС, т.к. они симметричны относительно вертикального диаметра окружности ТК. Следовательно, arccos a + arccos (- а) = АК + АТ = ТС + АТ =π. Из написанного равенства можно сделать вывод, что arccos (- а) = π– arccos a, где 0 ≤ а ≤ 1.
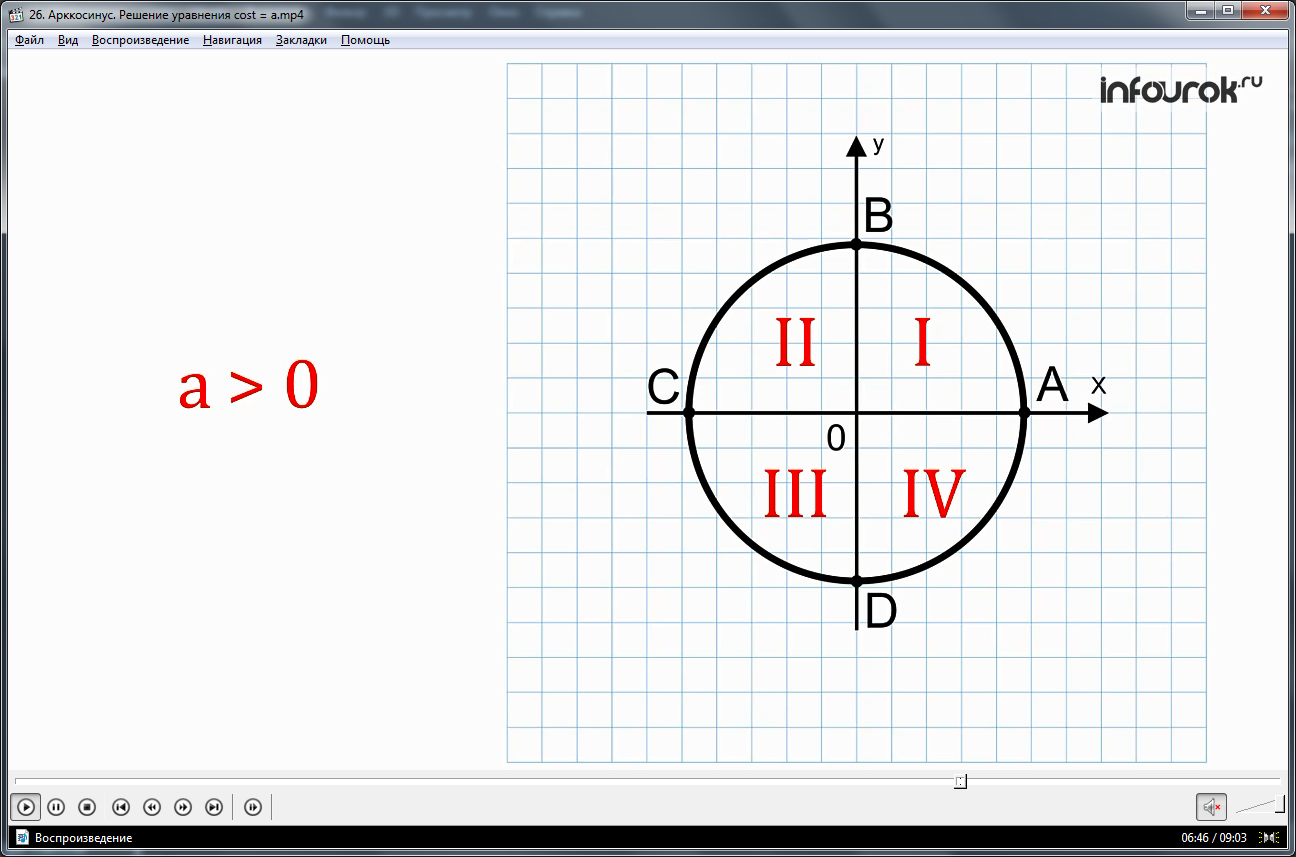
Когда а > 0, arccos a принадлежит I четверти окружности (отмечено на рисунке), а когда а < 0, arccos a принадлежит II четверти.
Рассмотрим еще один пример. Решить выражение, где cos t равен отрицательному числу. Запишем, чему в данном случае равно t.Тогда найдем величину арккосинуса, это 3π/4. Подставим найденное значение arcсos в значение t и получим, что t = ± 3π/4+ 2πk.
Разберем решение неравенства cos t. Для решения нам необходимо на числовой окружности найти точки, в которых х равен значению косинуса. Это точки со значениями π/4 и – π/4. Как видно на рисунке, длина дуги MN это – π/4≤ t ≤π/4. Значит ответом неравенства будет – π/4 + 2πk≤ t ≤ π/4+ 2πk.
ТЕКСТОВАЯ РАСШИФРОВКА:
Арккосинус. Решение уравнения cost = a
Рассмотрим решение уравнения cost = .
Учитывая, что cos t – это абсцисса точки М(t) (эм от тэ) числовой окружности, найдем на числовой окружности точки с абсциссой
На числовой окружности отметим точки М(t1), N(t2) – точки пересечения прямой х= с этой окружностью.
t1 – это длина дуги АМ, t2 - это длина дуги АN, t2 = – t1.
Когда математики впервые встретились с подобной ситуацией, они ввели новый символ arccos
arccos ( арккосинус одной четвертой).
Тогда t1 = arccos; t2 = - arccos
И тогда корни уравнения cost = можно записать двумя формулами:
t = arccos + 2πk, t = - arccos + 2πk или t = arccos + 2πk.
Что значит arccos ?
Это число
( длина дуги АМ), косинус которого равен одной четвертой и это число принадлежит первой четверти, то есть отрезку [0 ; ].
Теперь рассмотрим уравнение
cost = - . Аналогично решению предыдущего уравнения, запишем
t = arccos ) + 2πk.
Как понимать arccos( - )? Это число
( длина дуги АМ), косинус которого равен минус одной четвертой и это число принадлежит второй четверти, то есть отрезку [; ].
Дадим определение арккосинусу:
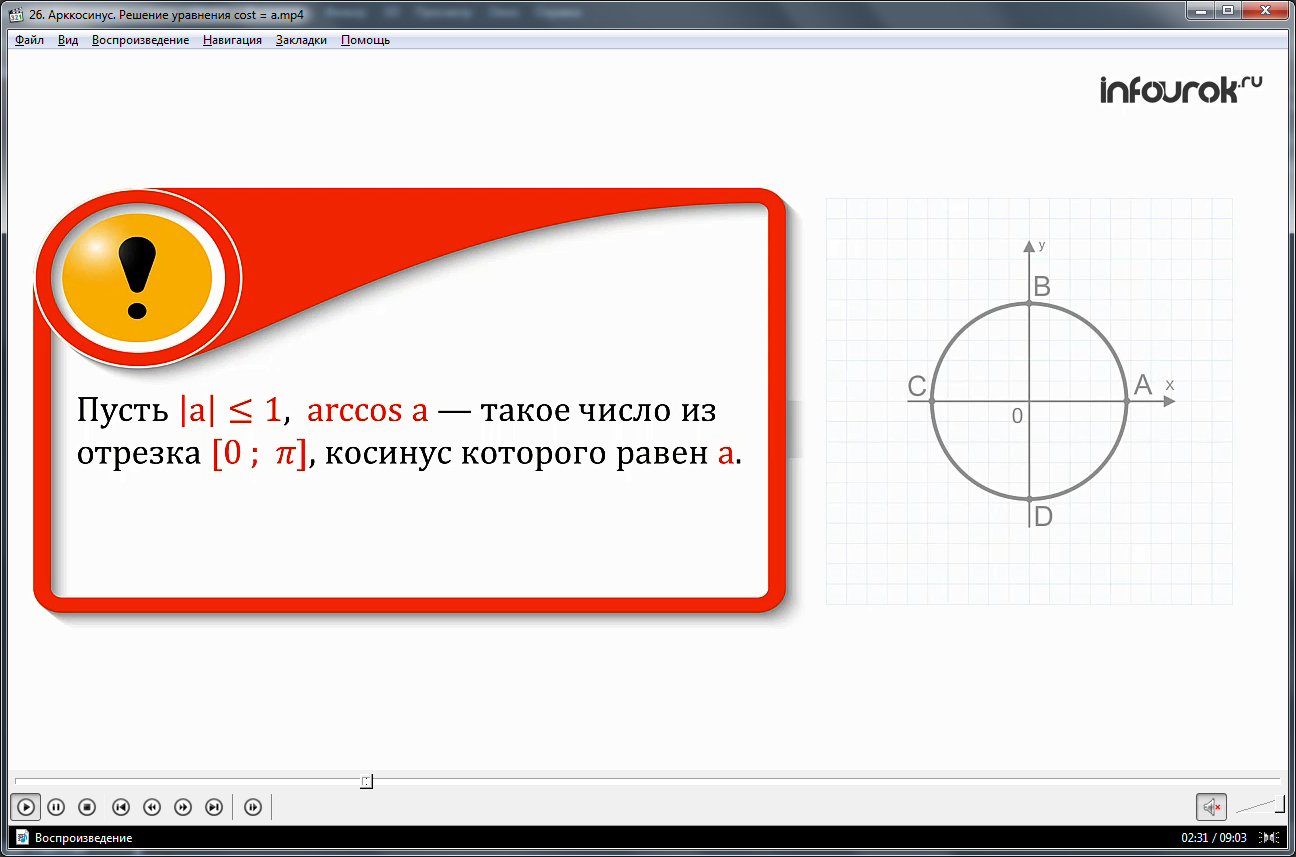
ОПРЕДЕЛЕНИЕ. Пусть | а | 1(модуль а меньше либо равно единице). Арккосинусом а называется такое число из отрезка [0 ; ], косинус которого равен а.(рис.1)
ПРИМЕР 1. Вычислить arсcos.( арккосинус корень из трех на два)
Решение. Пусть arсcos = t. Тогда cost = и t [ ; ]( тэ принадлежит отрезку от нуля до пи). Вспомним значению cos соответствует
(Показать таблицу значений) Значит, t = (пи на шесть), так как cos = и [0;π]. Значит, arсcos = .
arcos – это длина дуги, но длина дуги окружности это – t в определении cost
(Условно можно сказать что арккосинус это «значение угла», на который ушла точка от М от точки А, если вспомните то мы число t вводили как часть длины окружности, радиуса равного 1(одному), и тогда 2π– вся окружность равна 360°, π– половина окружности =180°, ==60°)

ПРИМЕР 2. Вычислить arсcos( - ( арккосинус минус корень из трех на два).
Решение. Пусть arсcos( - ) = t. Тогда cost = и t [ ; ]( тэ принадлежит отрезку от нуля до пи). Значит, t = (пять пи на шесть), так как cos = - и [; ]. Итак, arсcos ) = .
Докажем ТЕОРЕМУ. Для любого а [; ]( а из отрезка от минус единицы до единицы) выполняется равенство arccosа+ arccos(–а) = π( сумма арккосинуса а и арккосинуса минус а равна пи).
Доказательство. Для определенности будем считать, что а 0, тогда – а 0. На числовой окружности отметим arcos а ( это длина дуги АК) и
arccos(–а) ( это длина дуги АТ) ( смотри рис. 2)
Из доказанной теоремы следует: arcos (–а) = π – arcos а ( арккосинус минус а равен разности пи и арккосинуса а), где 0 а 1(где а больше либо равно нулю и меньше либо равно единице).
Когда а > 0, считают, что arcosа принадлежит первой четверти числовой окружности.
Когда а < 0 считают, что arcosа принадлежит второй четверти числовой окружности.
ПРИМЕР 3. Решить уравнение cost = - .
Решение. Составим формулу решений: t = arccos(- )+ 2πk.
Вычислим значения арккосинуса: arccos(- ) = π - arсcos = π - = .
( Согласно соотношению arccos(- ) = π - arсcos arсcos , то подставив данное значение в формулу, получим, что arccos(- ) = ) .
Подставим найденное значение в формулу решений t = arccos(- )+ 2πk и получим значение t: t = + 2πk.
ПРИМЕР 4.Решить неравенство cost .
Решение. Мы знаем, что cost – это абсцисса точки М(t) на числовой окружности. Это значит, что нужно найти такие точки М(t) на числовой окружности, которые удовлетворяют неравенству х .
Прямая х = пересекает числовую окружность в двух точках М и N.
Неравенству х соответствуют точки открытой дуги МN. Точке М соответствует , а точке N –
– (минус пи на четыре).
Значит, ядром аналитической записи дуги МN является неравенство
- t , а сама аналитическая запись дуги МN имеет вид
| Автор | |
|---|---|
| Дата добавления | 27.07.2014 |
| Раздел | Алгебра |
| Подраздел | Видеоурок |
| Просмотров | 13124 |
| Номер материала | 854 |