
Урок "Арксинус. Решение уравнения sint = a"

Краткое описание документа:
Аналогично теме в предыдущем видеоуроке рассмотрим уравнение sin t = a и его решение.
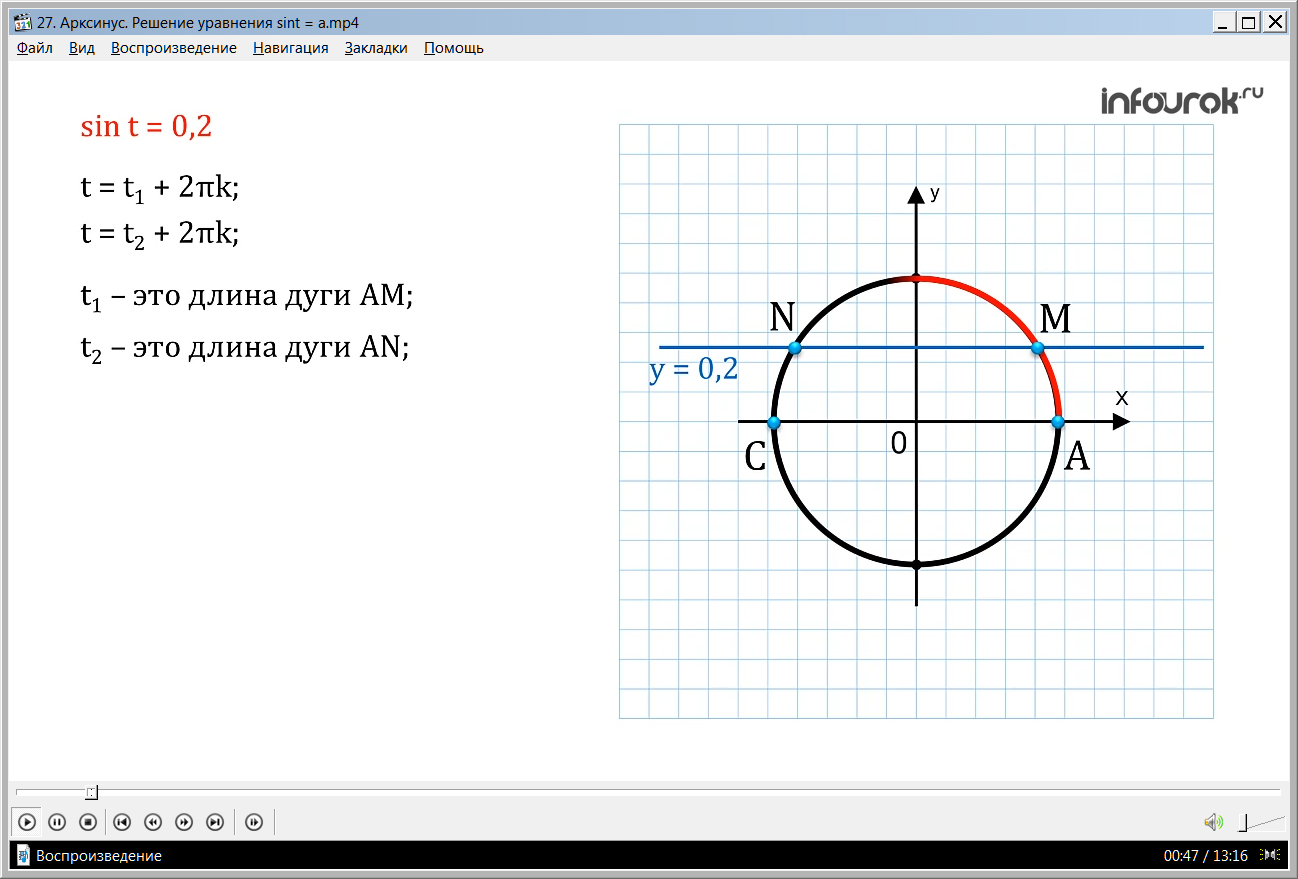
Рассмотрим пример – решение уравнения sin t =0,2. Используя числовую окружность на плоскости, найдем, что t1 и t2 – это длины дуг AM и AN соответственно. Значит, t = t1 + 2πk и t = t2 + 2πk.Найдем, что t2 = π – t1. Таким образом, arcsin 0,2 – это число (длина дуги АМ), синус которого равен 0,2, и это число принадлежит первой четверти числовой окружности, т.е. отрезку от 0 до π /2. Тогда корнями уравнения будут t = arcsin 0,2 + 2πk и t = π arcsin 0,2 +2πk.
Далее автор возвращается к понятию единичной числовой окружности. На окружности отмечена точка А. Поставим точку на окружности, которая будет соответствовать каждому действительному числу t в случаях: если t > 0, t < 0 и t = 0.
Сделаем вывод: числовая окружность – это окружность с определенным соответствием между действительными точками и точками окружности.
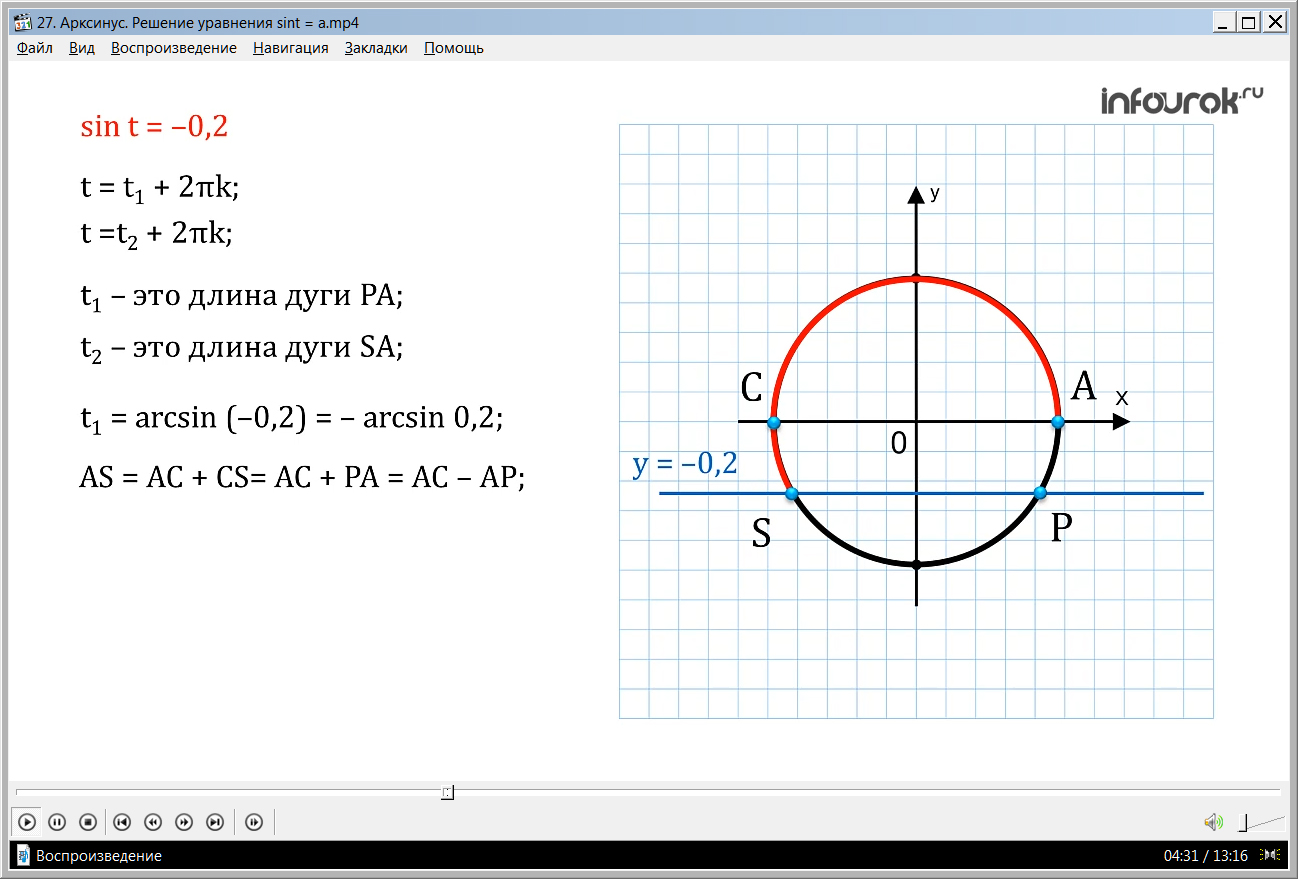
Следующий пример – решение уравнения sin t = – 0,2. Т.к. синус – число отрицательное, то точка движется по числовой окружности по часовой стрелке. , t = t1 + 2πk и t = t2 + 2πk. t1 – это длина дуги РА со знаком минус, а t2 – это длина дуги SA со знаком минус. Тогда t1 = arcsin (- 0,2) = – arcsin0,2. Заметим, что дуги АР и АМ равны, но противоположны по направлению. Далее показано, как получается ответ уравнения: t= arcsin (- 0,2)+ 2πk и t = π– arcsin (- 0,2)+ 2πk.
Дается определение арксинусу: если модуль а меньше или равен единице, то arcsin а это такое число из отрезка от – π/2 до π/2, синус которого равен а. Тогда выражение sin t = a при модуле а меньше или равном единице имеет 2 решения: t = arcsin a + 2πkи t = πarcsin a + 2πk. Указываются значения t при sin t = 0; sin t = 1; sin t = - 1.Для любого а из отрезка от минус одного до одного верно выражениеarcsin (- a) = - arcsin a, что проиллюстрировано на рисунке.
Теперь рассмотрим пример вычисления arcsin. Запишем, что arcsinданного значения равен, тогда sin t равен данному значению, где t принадлежит отрезку – π/2 до π/2.По таблице значений найдем, какое значение t соответствует значению sin t, это π/3. Значит, ответ уравнения будет π/3.
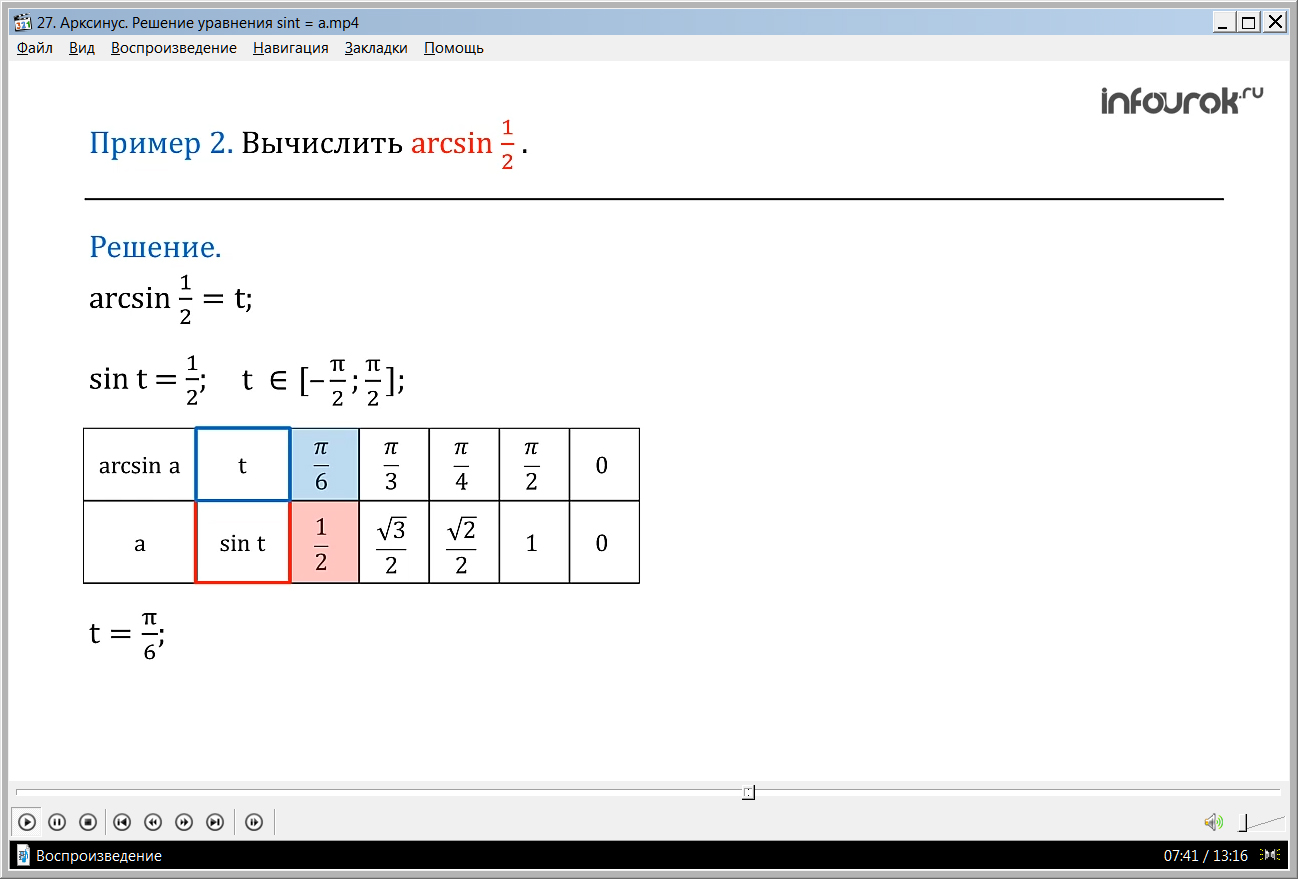
Перейдем ко второму примеру – вычисление arcsin 1/2. Укажем, что arcsin½ , тогда sin t = 1/2, где t принадлежит отрезку – π/2 до π/2.Пользуясь таблицей значений, запишем, что t =π/6. Значит, sin π/6 = 1/2, где π/6 принадлежит отрезку – π/2 до π/2.Ответ: arcsin1/2 = π/6.
Разберем следующий пример. Решить выражение, где sin t равен отрицательному числу.Запишем значения t. Далее запишем sin (- t) = - sin t. С помощью таблицы значений найдем, что t = –π/4. Подставив найденные значения в формулу, получим t = – π/4 + 2πk и t = 5π/4+2πk
Два решения t можно записать и одной формулой: t = (- 1)narcsin a + πn, где n – все действительные числа.
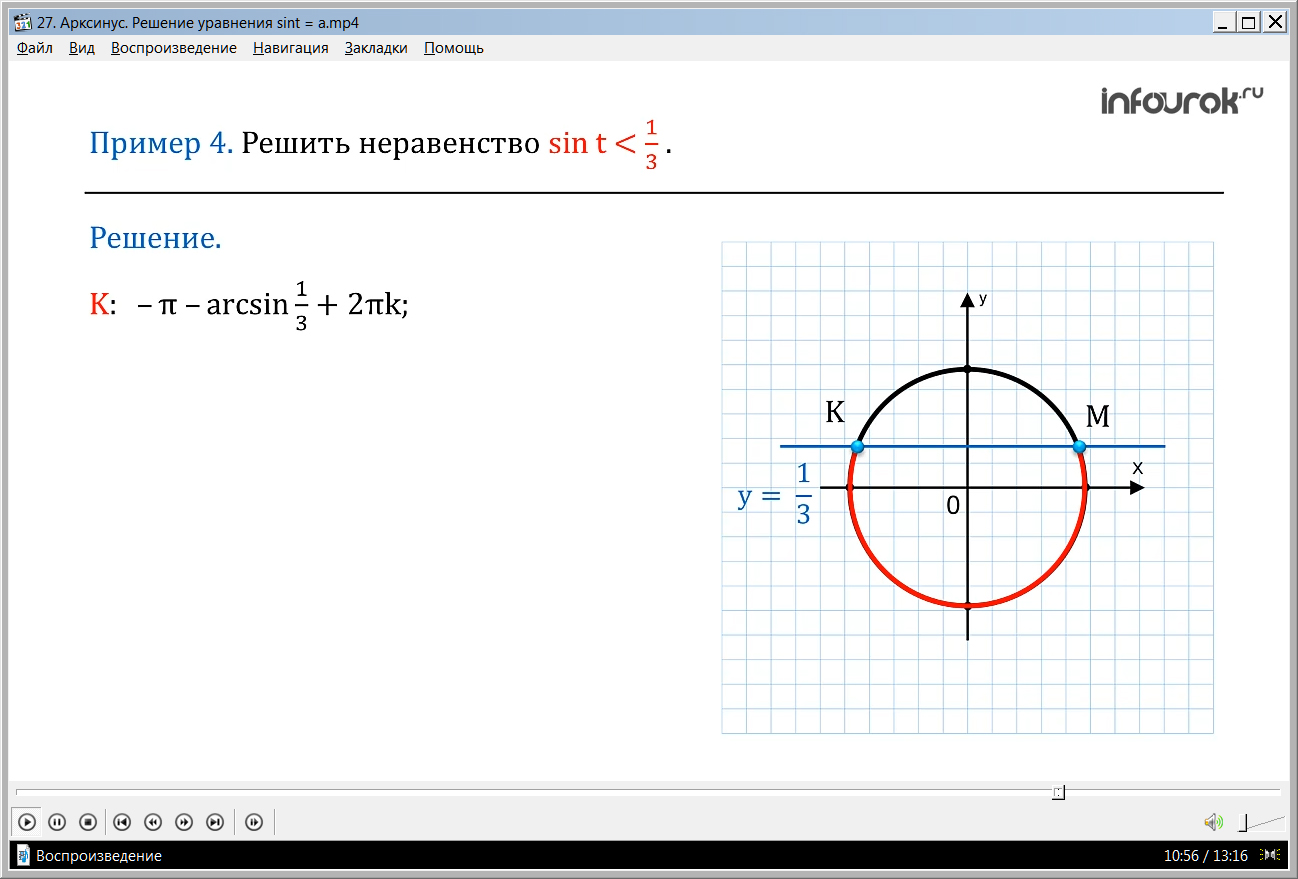
Помимо решения равенств, мы также можем решать тригонометрические неравенства. В качестве примера решим неравенство sin t < 1/3. Решениями неравенства будут точки на числовой окружности, в которых х =1/3. Это точки К и М, а решение неравенства – длина дуги КМ, как показано на рисунке. Запишем ответ: –π – arcsin1/3 + 2πk < t < arcsin1/3 + 2πk.
Для закрепления пройденной темы решим еще несколько выражений.
1) Вычислить sin (arcsin 3/16). Запишем, что arcsin 3/16 = t, тогда sin t = 3/16, где t принадлежит отрезкуот 0 до π/2. Получим sin (arcsin 3/16) = 3/16.
2) Вычислить cos (arcsin 5/13). Укажем, что arcsin 5/13 = t, тогда sin t =5/13, где t принадлежит отрезку 0 до π/2. Используя тождество sin2 t + cos2 t = 1, вычислим, что cos (arcsin 5/13) =12/13.
ТЕКСТОВАЯ РАСШИФРОВКА:
Арксинус. Решение уравнения sint = a.
Рассмотрим, как решаются уравнения с помощью числовой окружности.
Решим уравнения sint = 0,2 и sint = - 0,2.
Решение первого уравнения будет
t =t1 + 2πk; t =t2 + 2πk, где t1 – это длина дуги АМ, а t2 – это длина дуги АN.
Так как NC = АМ и АN=АС –NC, АС =π, то t2 = π - t1.
По аналогии с арккосинусом математики ввели для числа t1 новый символ: arcsin 0,2( арксинус ноль целых двух десятых). arcsin 0,2 мы будем понимать как число (длина дуги АМ), синус которого равен 0,2 и которое принадлежит первой четверти числовой окружности (т.е. отрезку [ 0;]).
Тогда корни уравнения sint = 0,2 можно записать в виде:
t = arcsin 0,2 + 2πk;
t =π - arcsin 0,2 + 2πk.
Вспомним определение единичной окружности
ОПРЕДЕЛЕНИЕ Дана единичная окружность, на ней отмечена начальная точка А – правый конец горизонтального диаметра. Поставим в соответствие каждому действительному числу t (тэ) точку окружности по следующему правилу:
1) Если t>0(тэ больше нуля), то, двигаясь из точки А в направлении против часовой стрелки (положительное направление обхода окружности), опишем по окружности путь АМ (а эм) длины t. Точка М и будет искомой точкой М(t) (эм от тэ).
2) Если t<0(тэ меньше нуля), то, двигаясь из точки А в направлении по часовой стрелке (отрицательное направление обхода окружности), опишем по окружности путь АМ (а эм) длины |t| (модуль тэ). Точка М и будет искомой точкой М(t) (эм от тэ).
3) Числу t = 0 поставим в соответствие точку А.
Единичную окружность с установленным соответствием (между действительными числами и точками окружности) будем называть числовой окружностью.
Решим уравнение sint = - 0,2.
ВСПОМНИМ
По определению Так как синус отрицательный то точка движется по единичной окружности по ходу часовой стрелки (смотри определение рис 2), и мы условились полученные углы брать со знаком минус, тогда получим:
С помощью числовой окружности: t =t1 + 2πk;
t =t2 + 2πk, где t1 – это длина дуги РА, взятая со знаком минус,
а t2 – это длина дуги SA, взятая тоже со знаком минус.
Число t1 обозначили символом
аrcsin( - 0,2) и заметили, что
аrcsin( - 0,2)= – arcsin 0,2( так как дуги РА и АМ (см рис 1 и 2) равны по длине и противоположны по направлению;
Математики также обратили внимание, что дугу AS по аналогии с первым примером можно получить как половина окружности минус арксинус числа минус а, покажем как это получитьAS= AC+CS=
= AC + PA = AC – AP
тогда ответ уравнения sint = - 0,2, можно записать аналогично с уравнение sint = 0,2, посмотрим как это выглядит
t2 = π - t1.
аrcsin (-0,2) мы будем понимать как число ( длина дуги АМ), синус которого равен –0,2 (минус ноль целых две десятые) и которое принадлежит четвертой четверти числовой окружности (т.е. отрезку
[;0] ).
Тогда корни уравнения sint = - 0,2 можно записать в виде:
t = arcsin(-0,2) + 2πk;
t =π – arcsin(-0,2) + 2πk.
Зная это определение, можно сделать общий вывод о решении уравнения
sint = a: если | а | 1, то уравнение sint = a имеет две серии решений:
t = arcsin а + 2πk; t =π – arcsin а + 2πk.
Для любого аϵ [–1; 1] ( а из отрезка от минус единицы до единицы) справедливо равенство аrcsin ( - а)= –arcsinа.( рис.1)
ПРИМЕР 1. Вычислить аrcsin.
Решение. Пусть аrcsin = t, тогда sint = и tϵ [–;]. Значит, t = , так как sin = (показать таблицу значений) и ϵ [–;].. Итак, аrcsin = .
ПРИМЕР 2. Вычислить аrcsin.
Решение. Пусть аrcsin = t, тогда sint = и tϵ [–;]. Значит, t = - , так как sin = показать таблицу значений и ϵ[–;]. Итак, аrcsin= .
ПРИМЕР 3.Решить уравнение sint = .
Решение.
1. Составим формулы решений:
t = arcsin + 2πk; t =π – arcsin + 2πk
2. Найдем значение арксинуса.
Так как sin (–t)=–sint= –, t= – (показать таблицу значений), то arcsin = - arcsin = .
3. Поставим найденное значение в формулы решений:
Тогда решение данного уравнения запишем в виде:
t = + 2πk; t =π –( )+ 2πk (выполним вычисления и получим) t = + 2πk.
Удобнее решение уравнения sint = a записывать не двумя формулами, а одной
( э равно минус единица в степени эн, умноженное на арксинус а и плюс пи ка).
Если n четное число, то при четных n = 2k получим первое решение t = arcsin а + 2πk, и перед. arcsina стоит знак «+»
Если nне счетное число, то при нечетных n= 2k+1 получим t = – arcsin а + π(2k+1)= π – arcsin а + 2πkи перед arcsin а стоит знак «-»,
а это второе решение уравнения.
Запишем решение примера 3 с помощью полученной формулы:
t = (- 1)n()+ πn =(– 1)n ∙( - 1) ∙ + πn = (–1)n+1 ·+ πn,
ПРИМЕР 4. Решить неравенство sint .
Решение. Вспомним, что sint – это ордината точки М(t), которая лежит на числовой окружности. То есть нам надо найти такие точки М(t)этой окружности, которые удовлетворяет неравенству у .
Прямая у пересекает числовую окружность в двух точках М и К. Неравенству у соответствуют точки открытой дуги КМ. Точке К соответствует - π – arcsin +2πk (минус пи минус арксинус одной третьей плюс два пи ка), а точке М arcsin +2πk (арксинус одной третьей плюс два пи ка). Следовательно, решение неравенства запишем в виде:
- π – arcsin +2πk t arcsin +2πk ( тэ больше, чем минус пи минус арксинус одной третьей плюс два пи ка, но меньше, чем арксинус одной третьей плюс два пи ка).
ПРИМЕР 5. Вычислить sin( arcsin ) ( синус арксинуса трех шестнадцатых).
Решение. Воспользуемся определением арксинуса. Пусть arcsin = t, тогда sint = , причем tϵ [;. Получили sin (arcsin)= sint =.
ПРИМЕР 6. Вычислить cos(arcsin) (косинус арксинуса пяти тринадцатых).
Решение. Пусть arcsin = t, тогда sint = , причем tϵ[0; ].
Используя основное тригонометрическое тождество (sin2t + cos2t = 1), выразим значение cos2t:
cos2t = 1- sin2t, т.к. sin2t =)2 ; тогда cos2t = 1 - ;выполним вычисления и получим cos2t = ; извлечем квадратный корень cost = или cost = –
Так как tϵ[0; ]. ( тэ принадлежит первой четверти), то косинус положительный, т.е. cos(arcsin).
| Автор | |
|---|---|
| Дата добавления | 27.07.2014 |
| Раздел | Алгебра |
| Подраздел | Видеоурок |
| Просмотров | 9667 |
| Номер материала | 855 |