
Урок «Дробно-линейная функция и ее график»

Краткое описание документа:
Дробно-линейная функция изучается в 9 классе после того, как изучены некоторые другие виды функций. Именно об этом говорится в начале урока. Здесь речь идет о функции y=k/x, где k>0. По словам автора, дана функция рассматривалась школьниками ранее. Поэтому с ее свойствами они знакомы. Но одно свойство с указанием особенностей графика этой функции автор предлагает вспомнить и рассмотреть подробно на этом уроке. Это свойство отражает прямую зависимость значения функции от значения переменной. А именно, при положительном x, стремящемся к бесконечности, значение функции также положительно и стремится к 0. При отрицательном x, стремящемся к минус бесконечности, значение y – отрицательно и стремится к 0.
Далее автор отмечает, как это свойство проявляется на графике. Так постепенно обучающиеся знакомятся с понятием асимптоты. После общего ознакомления с этим понятием следует его четкое определение, которое выделено яркой рамкой.
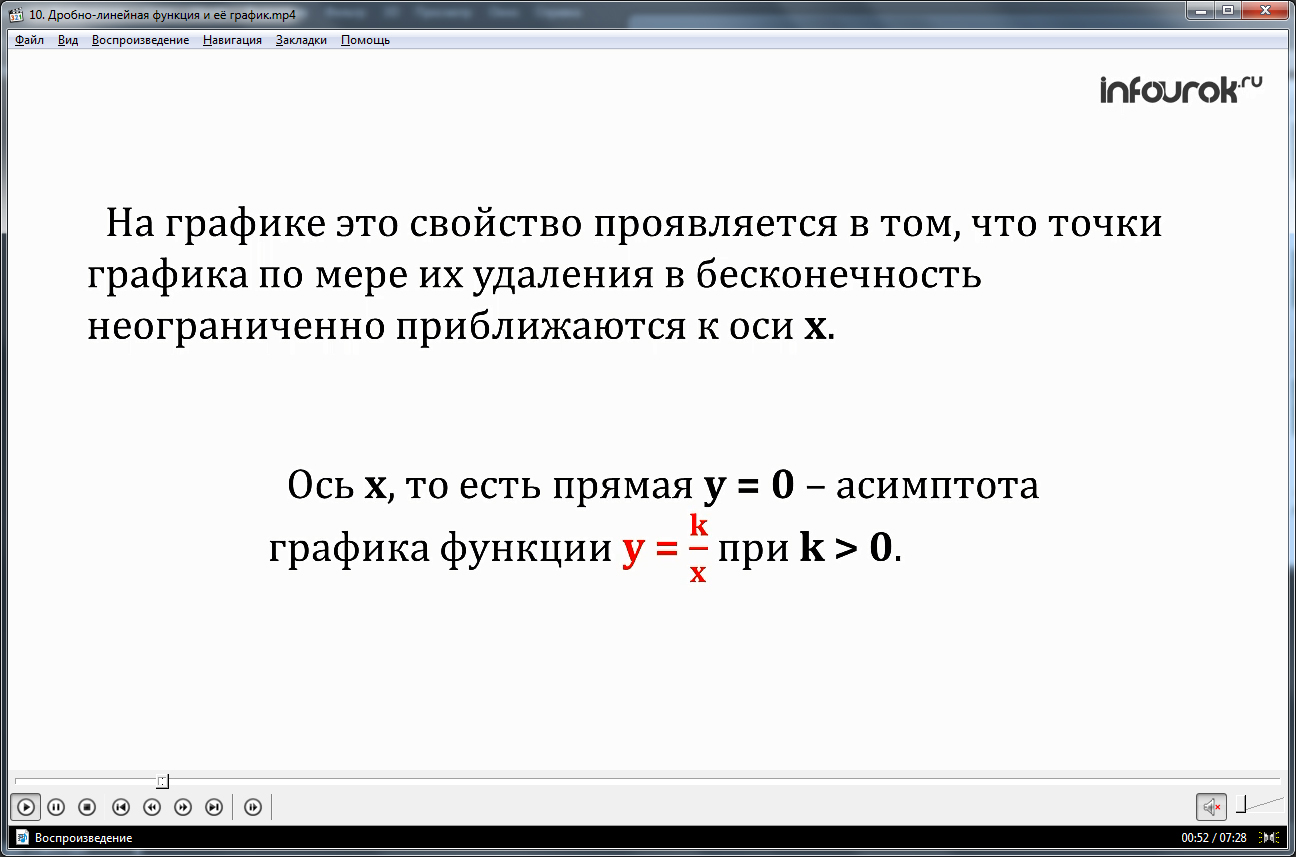
После того, как введено понятие асимптоты и после его определения автор обращает внимание на то, что гиперболы y=k/xпри k>0 имеет две асимптоты: это оси xи y. Точно такая же ситуация и с функцией y=k/xпри k<0: функция имеет две асимптоты.
Когда основные моменты подготовлены, знания актуализированы, автор предлагает перейти к непосредственному изучению нового вида функций: к изучению дробно-линейной функции. Для начала предлагается рассмотреть примеры дробно-линейной функции. На одном таком примере автор демонстрирует, что в качестве числителя и знаменателя выступают линейные выражения или, другими словами, многочлены первой степени. В случае числителя может выступать не только многочлен первой степени, но и любое число, отличное от нуля.

Далее автор переходит к демонстрации общего вида дробно-линейной функции. При этом он подробно расписывает каждый компонент записанной функции. Также поясняется, какие коэффициенты не могут быть равны 0. Эти ограничения автор расписывает и показывает, что может произойти, если эти коэффициенты окажутся нулевыми.
После этого автор повторяет, как получается график функции y=f(x)+nиз графика функции y=f(x). Урок на данную тему можно также найти в нашей базе. Здесь же отмечается то, как построить из этого же графика функции y=f(x) график функции y=f(x+m).
Далее автор отмечает, что графиком дробно-линейной функции является гипербола. Это предлагается показать на рисунке. А именно, как этот график получается из гиперболы y=k/xс помощью параллельных переносов.

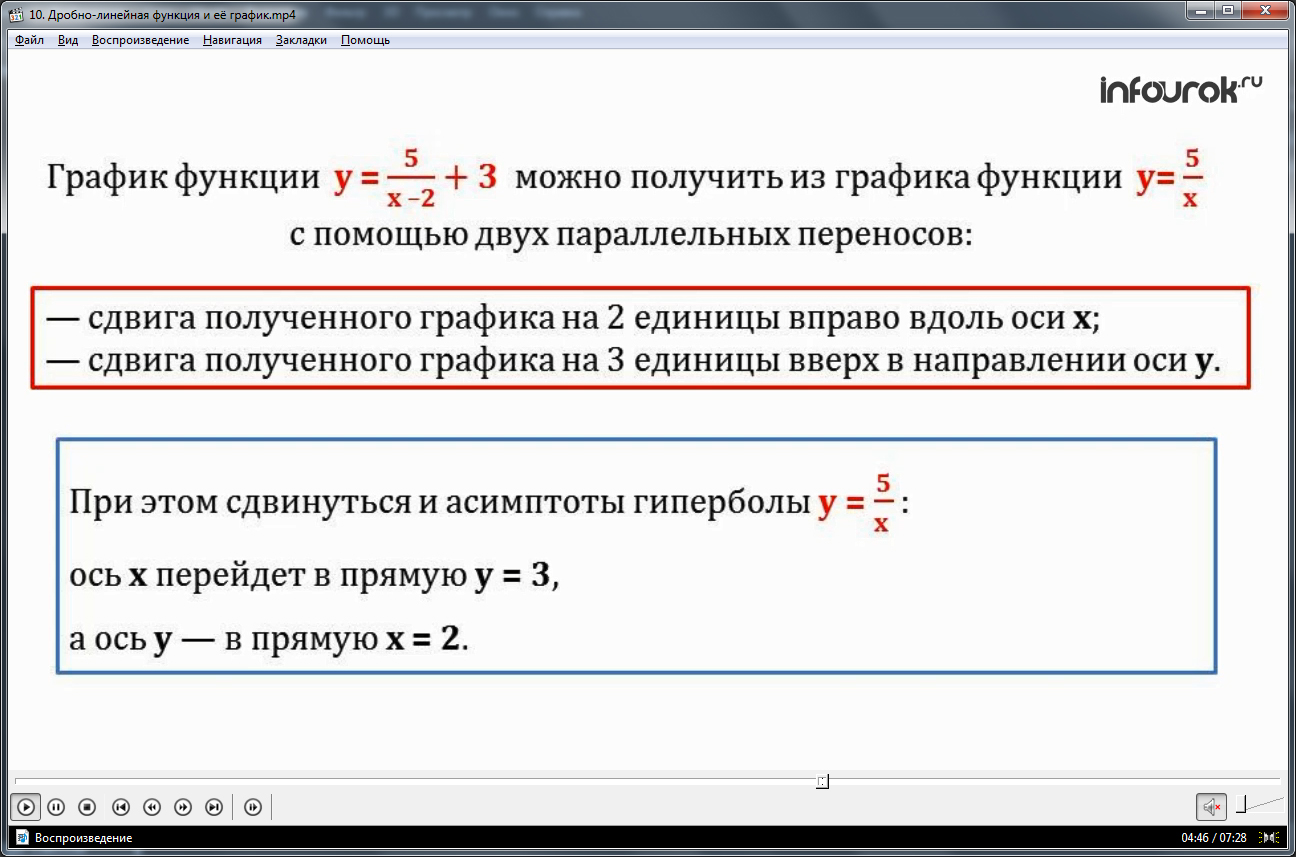
Все это демонстрируется на конкретном примере. Здесь предлагается построить график определенной функции. Все построение идет поэтапно. Для начала предлагается выделить из данной алгебраической дроби целую часть. Выполнив необходимые преобразования, автор получает целое число, которое прибавляется к дроби с числителем, равным числу. Так график функции, которая представляет собой дробь, можно построить из функции y=5/xпосредством двойного параллельного переноса. Здесь же автор отмечает, как переместятся асимптоты. После этого строится система координат, переносятся асимптоты на новое местоположение. Затем строятся две таблица значений для переменной x>0 и для переменной x<0. Согласно полученным в таблицах точкам, на экране ведется построение графика функции.
Далее рассматривается еще один пример, где перед алгебраической дробью в записи функции присутствует минус. Но это ничем не отличается от предыдущего примера. Все действия проводятся аналогичным образом: функция преобразовывается к виду, где выделяется целая часть. Затем переносятся асимптоты, и строится график функции.
На этом объяснение материала заканчивается. Длится этот процесс 7:28 минут. Примерно столько времени требуется учителю на обычном уроке для объяснения нового материала. Но для этого необходимо заранее хорошенько подготовится. Но если взять за основу данный видеоурок, то подготовка к уроку займет минимум времени и сил, а обучающимся понравится новый метод обучения, предлагающий просмотр видеоурока.
| Автор | |
|---|---|
| Дата добавления | 29.08.2014 |
| Раздел | Алгебра |
| Подраздел | Видеоурок |
| Просмотров | 9480 |
| Номер материала | 682 |