
Урок «Движения. Центральная симметрия»

Краткое описание документа:
ТЕКСТОВАЯ РАСШИФРОВКА УРОКА:
Мы начинаем знакомство с понятием движение в пространстве.
В курсе планиметрии вы уже познакомились с понятием движения — это такое отображение плоскости, при котором сохраняется расстояние между точками.
Говорят, что задано отображение пространства на себя, если каждой точке К пространства поставлена в соответствие некоторая точка К1, причём любая точка К1 пространства оказалась поставленной в соответствие какой-либо точке К.
Принято говорить, что при таком отображении точка К отображается (переходит) в точку К1.
Отметим, что особую роль в геометрии играют отображения пространства на себя, сохраняющее расстояние между точками. Они называются движениями пространства.
Таким образом, если при движении пространства точки А и В переходят (отображаются) в точки А1 и В1 ,то АВ=А1В1.
Одним из примеров движения служит центральная симметрия — это такое отображение пространства на себя, при котором любая точка К переходит в симметричную ей точку К1, относительно центра симметрии точки В.
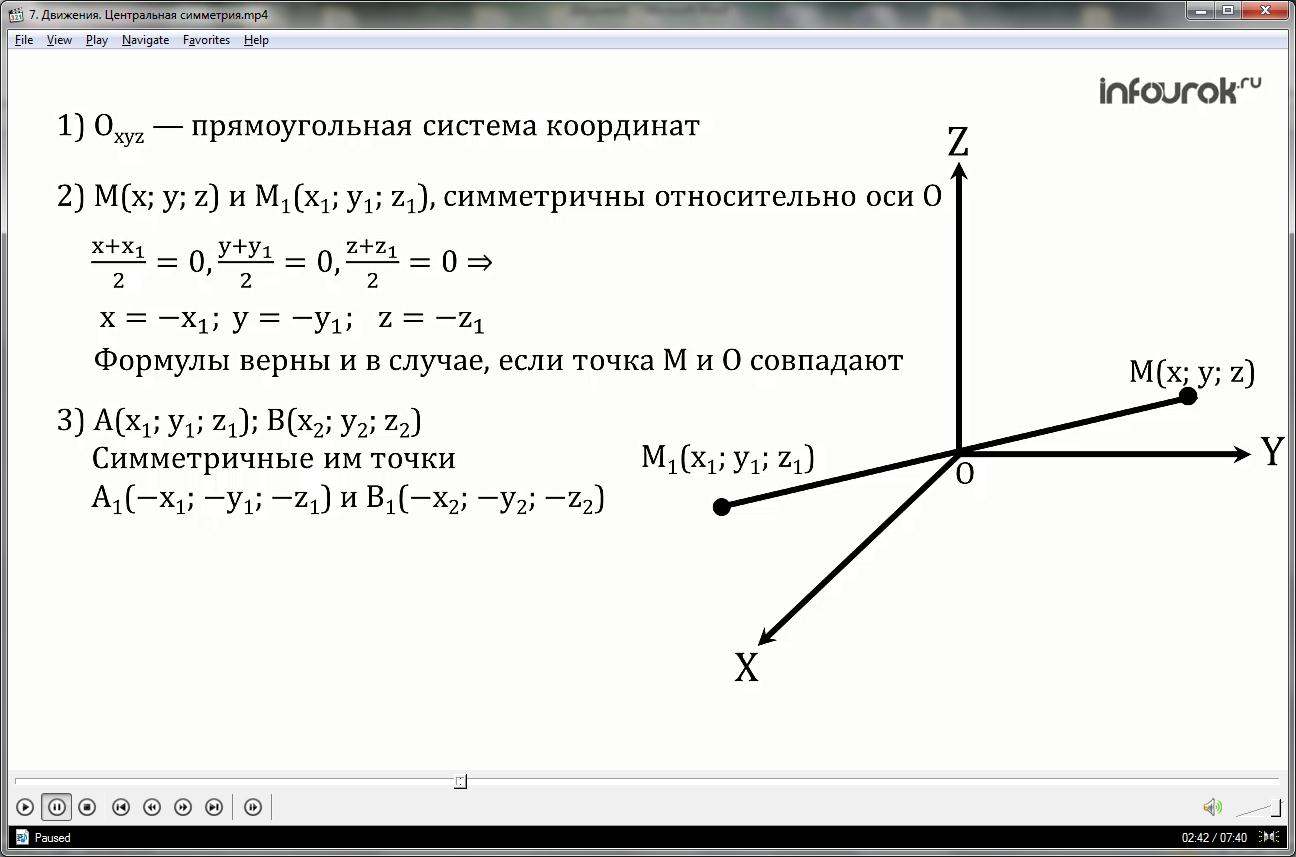
1. Обозначим буквой О центр симметрии и введём декартову (прямоугольную) систему координат Оxyz с началом в точке О.
2.Найдем связь между точками М(x;y;z) и M1(x1;y1;z1), которые симметричны относительно точки О.
В случае, если М не совпадает с центром симметрии О, то О является серединой отрезка ММ1.Тогда по формулам координат середины отрезка найдём:
x+x1 =0; y +y1 =0; z +z1 =0
Откуда:
x=-x1 ; y=-y1; z=-z1
Данные формулы верны и в случае, когда М и О совпадают (объясните самостоятельно).
3.Рассмотрим любые две точки: А — с координатами (x1;y1;z1) и В — с координатами (x2;y2;z2) и докажем, что расстояние между точками А1 и В1, которые им симметричны, равно АВ.
По доказанному выше, имеем, что точки А1 и В1 имеют координаты: А1 (-x1;-y1;-z1) и В1 (-x2;-y2;-z2).
По формуле расстояний между двумя точками, найдём:
АВ=√(х2-х1)2+(y2-y1)2+(z2+z1)2
A1B1=√(-х2-х1)2+(-y2-y1)2+(-z2+z1)2,
Очевидно, что АВ=A1B1, то есть расстояние между точками сохранено.
Таким образом, мы доказали, что центральная симметрия является движением.
Применим полученные знания при решении задач.
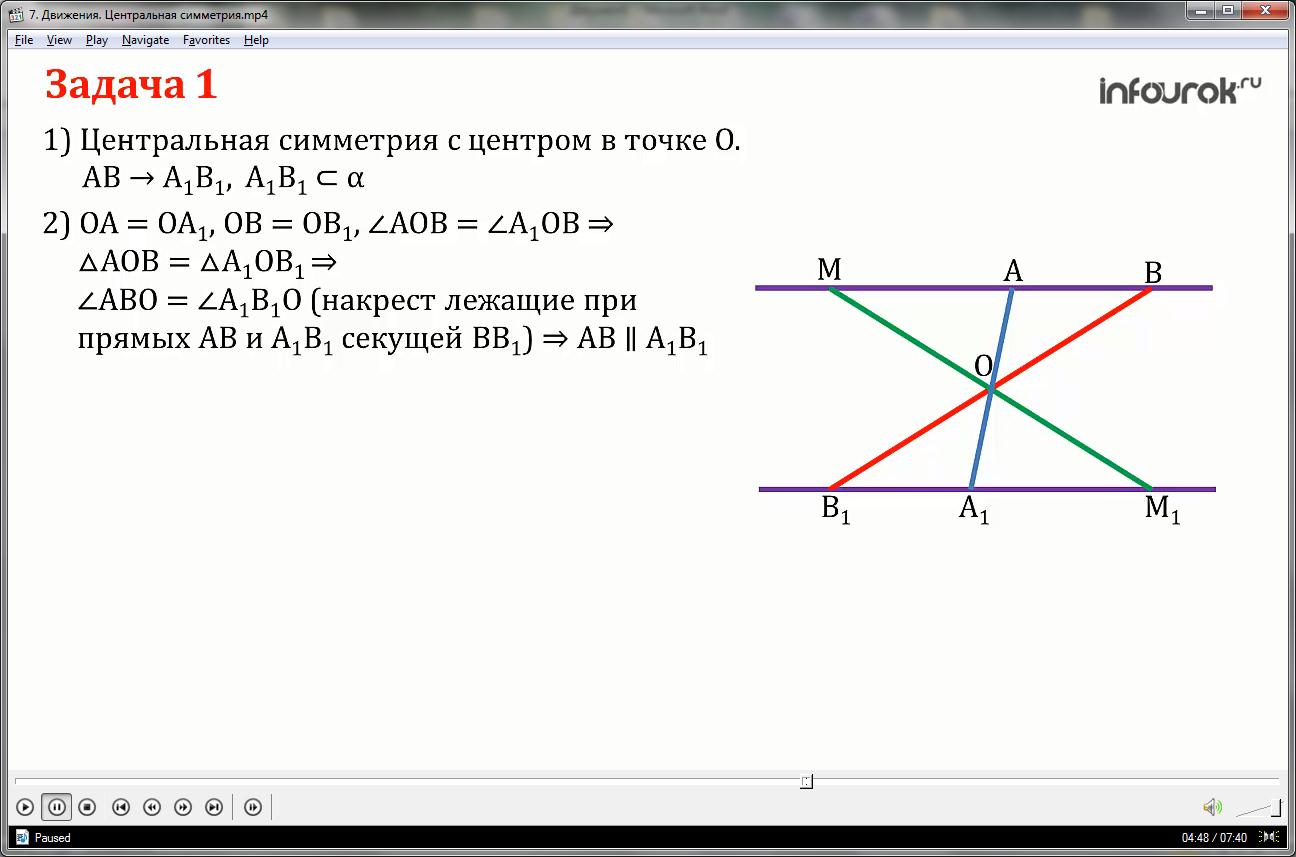
Задача 1.
Доказать, что при центральной симметрии прямая, не проходящая через центр симметрии, отображается на параллельную ей прямую.
1. Рассмотрим центральную симметрию пространства с центром в точке О и произвольную прямую АВ, не проходящую через эту точку.
Прямая АВ и точка О определяют единственную плоскость α. Точки А и В отображаются при центральной симметрии в точки А1 и В1, которые так же лежат в плоскости α. А значит, и вся прямая А1 В1 лежит в плоскости α.
2. Докажем, что прямые АВ и А1В1 параллельны.
Так как симметрия центральная, то ОА=ОА1, ОВ=ОВ1, угол АОВ равен углу А1ОВ1 — как вертикальные, значит треугольник АОВ равен треугольнику А1ОВ1 по первому признаку равенства треугольников.
Из равенства треугольников следует, что угол АВО равен углу А1В1О, то есть равны накрест лежащие углы при пересечении прямых АВ и А1В1 секущей ВВ1, следовательно прямые АВ и А1В1 параллельны.
3. Докажем теперь, что при центральной симметрии с центром в точке О прямая АВ отображается на прямую А1В1. Для этого нужно доказать, что произвольная точка М прямой АВ переходит в некоторую точку М1 прямой А1В1 и наоборот: произвольная точка прямой А1В1 симметрична некоторой точке прямой АВ.
Возьмём на прямой АВ какую-либо точку М, отличную от А, и проведём прямую МО. Эта прямая пересечёт прямую А1В1 в какой-то точке М1.

Симметрия центральная, значит АО=ОА1; угол МОА равен углу М1ОА1, как вертикальные; угол МАО равен углу М1А1О, как накрест лежащие при параллельных прямых АВ и А1В1 и секущей ВВ1. Значит, треугольники МАО и М1А1О равны по второму признаку равенства треугольников. Из равенства треугольников следует, что отрезки МО и ОМ1 равны, а это значит, что точка М переходит в точку М1 , лежащую на прямой А1В1 при симметрии относительно точки О.
Аналогично доказывается обратное: любая точка М1 прямой А1В1 симметрична некоторой точке М прямой АВ относительно точки О.
Итак, при симметрии с центром О прямая, не проходящая через точку О, отображается на параллельную прямую.
Сегодня мы показали, что отображение пространства на себя, сохраняющее расстояние между точками, является движением, а так же убедились, что при движении отрезок переходит в равный ему отрезок, прямая — в прямую, плоскость — в плоскость. Примером этому служит центральная симметрия.
| Автор | |
|---|---|
| Дата добавления | 07.11.2014 |
| Раздел | Геометрия |
| Подраздел | Видеоурок |
| Просмотров | 10290 |
| Номер материала | 993 |